Extrempunkter, Extremvärden och begreppsröran

2013-01-31 Av Simon Rybrand 3 kommentarer

En tid in i inlärningen av derivata (matematik C eller matematik 3) så dyker det upp en storm av olika begrepp kopplade till derivata och kurvor.

Då stöter du säkert begreppen extrempunkter, maximipunkter, minimipunkter, terrasspunkter, extremvärden, lokala minimipunkter, lokala minimivärden, lokala maximipunkter, lokala maximivärden, globala minimivärden, globala maximivärden, globala minimipunkter, globala maximipunkter och minsta och största värde.

Pjuuh! Många begrepp helt enkelt. Det är inte konstigt om det mesta flyter ihop till en stor otillgänglig begreppsröra.

Det går förstås inte att lära sig allt på en gång. Istället får man träna och försöka se likheter och skillnader och hela tiden gå tillbaka till beskrivningar av begreppen. Det här blogginlägget tänkte jag kunde bli en bra startpunkt för detta så att du kan gå tillbaka hit och kika för att friska upp minnet när du räknar på liknande problem.

Begrepp som slutar på punkt

Låt oss först lyfta fram skillnaden på punkt och värde. En punkt är ju en koordinat med ett x – värde och ett y – värde, t.ex. (3, 4). Så när vi pratar om de olika typerna av extrempunkter nämligen maximipunkt, minimipunkt och terasspunkt så söker man eller beskriver själva punkten.

Begrepp som slutar på värde

Med värde, t.ex. olika extremvärden så är det istället y – värdet som beskrivs eller söks. Det här kallas också ibland för funktionsvärde men är alltså samma sak som y – värdet.

Maximi-, minimi- och terrasspunkter

I en maximi-, minimi- eller terrasspunkt så är antingen derivatan noll eller så befinner vi oss i ändpunkten av ett intervall.

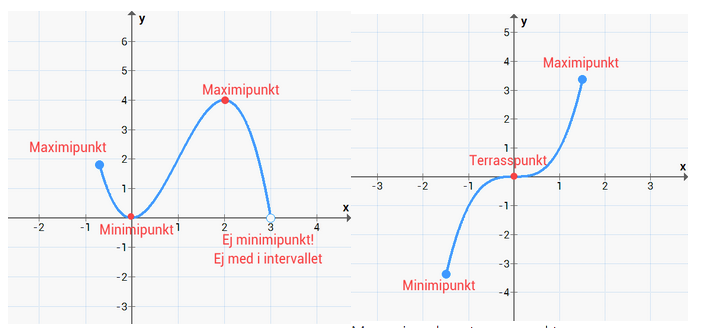
För ändpunkten av ett intervall gäller att det är en minimipunkt om kurvan är på väg neråt och att det är en maximipunkt om kurvan är på väg uppåt. Viktigt att nämna är också att ändpunkterna av ett intervall endast kan vara en maximi eller minimipunkt om det är inkluderat, t.ex om x ≤ 3 men inte om x < 3.

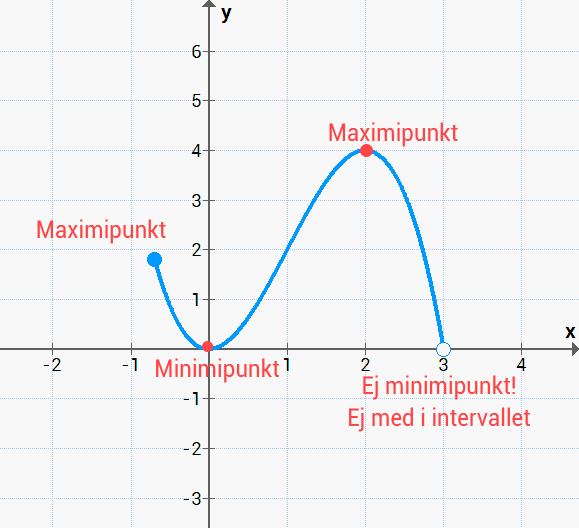Maximi och minimipunkter

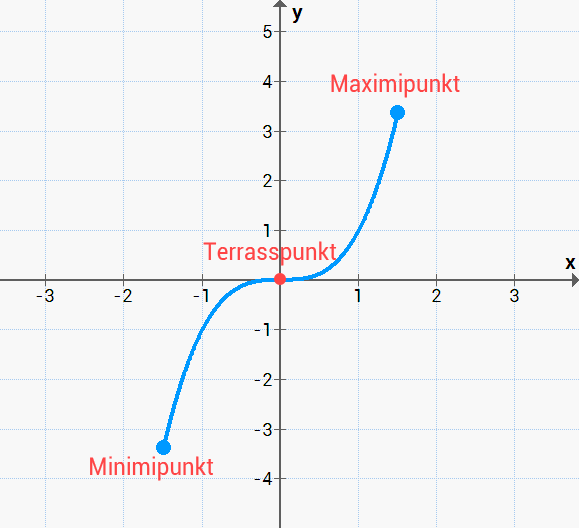Max, min och en terrasspunkt

Skillnaden på lokalt och globalt

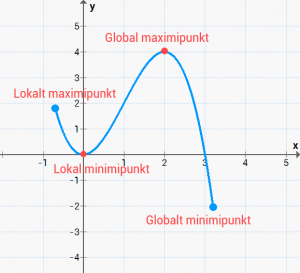För att krångla till det lite extra så finns det även lokala och globala värden/punkter. Med det här menas att man gör skillnaden på om punkten har det största y – värdet av alla extremvärden eller extrempunkter eller inte. Om punkten/värdet har det största y – värdet så är denna global, annars så är den lokal.

Lista på begrepp kopplade till Extrempunkter och Extremvärden

Kanske har du vid det här laget i alla fall en känsla för vilka olika punkter och värden som vi pratar om. För att göra det här så tydligt som möjligt så listar vi även här nedan en förklaring av alla de begrepp som vi nämnt i det här blogginlägget.

• Extrempunkt – En punkt (x, y) som är en lokal maximipunkt eller en lokal minimipunkt och där är derivatan noll. Här gäller att en terrasspunkt inte är en lokal max/min punkt och är därmed inte en extrempunkt.
• Maximipunkt – En punkt där derivatan är positiv innan punkten, noll i punkten och negativ efter. En maximipunkt kan också vara slutet av ett intervall om punkten är inkluderad i intervallet och kurvan är på väg uppåt.
• Minimipunkt – En punkt där derivatan är negativ innan punkten, noll i punkten och positiv efter. En minimipunkt kan också vara slutet av ett intervall om punkten är inkluderad i intervallet och kurvan är på väg nedåt.
• Extremvärde – Y värdet för en extrempunkt.
• Maximivärde – Y värdet för en maximipunkt.
• Minimivärde – Y värdet för en minimipunkt.
• Globalt extremvärde – Det största eller minsta y – värdet av alla extrempunkter.
• Lokalt extremvärde – Ett maximivärde eller minimivärde.
• Största värdet – Det största y – värdet i ett intervall.
• Minsta värdet – Det minsta y – värdet i ett intervall.