Köningsbergs 7 broar och grafteori
2014-02-10 Av Simon Rybrand 0 kommentarer
För några veckor sedan släppte vi kursen till Matte 5 här på MatematikVideo och denna har nu även fått sin första påfyllning av videos på området grafteori. Jag tänkte därför blogga lite om just detta område och då särskilt de broar som till viss del har varit orsaken till att grafteorin har skapats.
Köningsbergs 7 broar och Euler
Det klassiska problem som i mångt och mycket gav upphov till grafteorin kallas för Köningsbergs 7 broar. Det var nämligen så att man i staden Köningsberg (nuvarande Kaliningrad) funderade på följande fråga i staden:
”Går det att passera alla broar som binder samman de två öarna med fastlandet utan att passera varje bro mer än en gång?”
Ingen hade under sin söndagspromenad över broarna hittat ett sätt att genomföra denna typ av vandring genom staden.
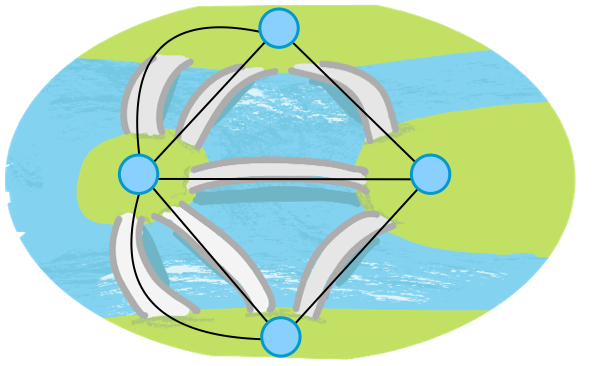
När Leonard Euler (Schweizisk matematiker) fick höra talas om problemet bestämde han sig för att försöka undersöka om detta var möjligt. Det han då gjorde var att rita en slags schematisk bild över broarna (det som kom att kallas grafer) för att på detta vis få en bra överblick över hur dessa kopplades samman. Det var inte bara smart ur bekvämlighetsperspektiv (han slapp vandra fram och tillbaka) utan gjorde också att han kunde bevisa att denna promenad faktiskt var omöjlig.
Det han visade var att om det finns två eller flera noder som har ett ojämnt antal kanter så är det omöjligt att genomföra en sådan vandring.
Numera är faktiskt denna vandring möjlig men inte för att Eulers bevis inte stämde. Istället raderade andra världskriget två av broarna och en ny bro byggdes vilket möjliggjorde vandringen.
Eulerväg, Eulerkrets och grafteori
En väg som beskriver en vandring enligt problemet ovan kallas för en Eulerväg. Om vandringen också skall starta och sluta i samma hörn (kallas också för nod) så kallas denna vandring istället för en Eulerkrets. Detta är alltså det man inom grafteorin kallar för en sluten vandring då man startar och slutar i samma hörn.
Detta problem är alltså en av orsakerna till att vi idag jobbar med området grafteori i kursen matematik 5. Man kan tycka att det faktiskt inte verkar vara så stor praktisk nytta med att förstå detta område. Men grafteorin innehåller numera en rad andra tillämpningar som faktiskt kan komma till användning. Exempelvis kan man med grafteori bygga upp metoder för att hitta kortaste vägar mellan orter eller för att minimera kostnader.
Läs mer om matematik och kända problem
- Primtal, Eratosthenes såll och att få betalt för primtal
- Kotten och Fibonacci
- Get eller Bil – Monty Hall problemet