Monty Hall problemet – get eller bil?
2013-02-15 Av Simon Rybrand 2 kommentarer
Det finns ett rätt kul problem inom sannolikhetsläran som kallas för Monty Hall problemet och är döpt efter en amerikansk programvärd i ett TV program som hette Lets make a deal. Problemet, som visserligen bara är löst baserat på programmet, är följande:
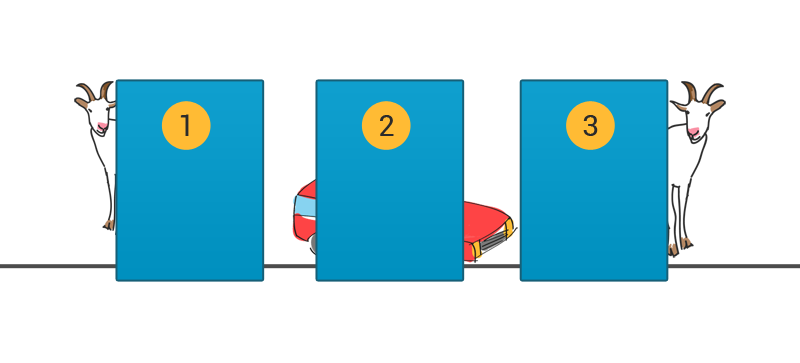
En programvärd ger dig möjligheten att välja mellan tre stycken olika dörrar. Bakom en av dessa dörrar finns en bil och bakom de andra två finns varsin get (?!). Du väljer först en dörr. När du valt denna dörr så öppnar programvärden en av de andra två dörrarna. Han väljer alltid en av dörrarna där det finns en get bakom denna. Frågan är nu om du skall byta dörr eller hålla kvar vid den du har valt?
OBS, Läs inte vidare härifrån om du vill fundera på svaret själv först.
Lösningen på problemet, en fråga om sannolikheter
Man tycker vid sin första tanke på problemet att det nog egentligen inte spelar någon roll om du håller fast vi den dörr som du har valt eller byter. Men saken är den att det faktiskt är högre sannolikhet att få bilen om du byter dörr. Det här kan beskrivas med hjälp av att dela upp dina val i tre stycken möjliga scenarier där två av dessa ger vinst.
- Låt säga att du redan har valt bilen vid ditt första val. Byter du då kommer du förstås att få en get istället (vilket kanske inte är så dumt det heller) och du har förlorat.
- Låt säga att du inte har valt bilen utan den första geten. Programledaren kommer då att öppna en av de dörrar där det finns en get. Byter du då så kommer du att välja bilen och du har vunnit.
- Låt säga att du valde den andra geten vid ditt första val. Återigen så kommer programledaren att välja den dörr där det finns en get och byter du då så vinner du även i detta scenario.
Summa summarum, det finns alltså två av tre (2/3) scenarier där du tjänar på att byta dörr. Du ger dig alltså större sannolikhet att vinna genom att byta dörr.
Knäckte du problemet innan du hade läst förklaringen?
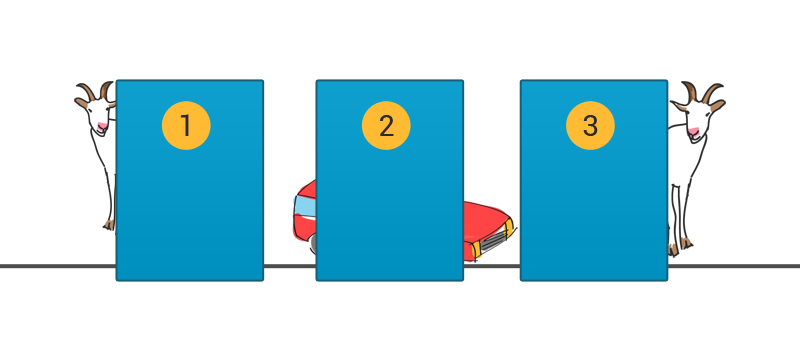
Ännu lättare att tänka så här.
Varje dörr har sannolikheten 1/3 för vinst. Det betyder samtidigt att de två dörrar som du inte väljer, tillsammans har sannolikheten 2/3 för vinst.
Fråga dig nu vad som ger dig störst chans till vinst: att få spela med två dörrar eller med en? Svaret har vi redan kommit fram till: det är dubbelt så hög vinstchans att spela med två dörrar.
Hur kan jag då spela med de två dörrarna som jag inte valde från början och därmed fördubbla mina vinstchanser?
Lösningen inleds med att låta spelledaren öppna en de två dörrarna som du inte valde från början. Därmed har du spelat med den första av de två dörrarna som du inte valde från början.
Men du vill ju även spela med den andra av de två dörrarna som du inte valde från början?
För att kunna göra det måste du därför byta till den återstående dörren. När också den öppnas har du spelat med de två dörrarna som du inte valde från början.
Vilket var precis vad du ville göra.
Det finns ett annat sätt att förklara detta som är enklare.
Tittar man närmare på reglerna så inser man att det inte är ett val 1 av 3 (= 1/3 chans) utan spelet är faktiskt ”välj 2 dörrar och om en av dessa är rätt får du bilen” (= 2/3 chans). ”Bytaren” inser detta och satsar exempelvis på dörr 1 och 2, säger sedan 3 till programledaren varvid denne blir tvungen att tala om vilken av 1 eller 2 som är fel. Alltså alltid 2/3 chans för ”bytaren”.
Problemet är alltså att det från början framställs på ett som gör att man psykologisk uppfattar det som 1/3 chans oavsett vad som händer och blir ”icke bytare”.