Oändlighet – vad är det matematiskt?

2013-01-21 Av Simon Rybrand 2 kommentarer

I gymnasieskolan råkar man ofta komma i kontakt med begreppet oändlighet vid diskussioner kring huruvida man egentligen kan dividera med noll (länk). Men det kan ju också vara intressant att diskutera hur matematiker egentligen beskriver det här begreppet.

Några tankar om oändlighet

Begreppet oändlighet är lite som en hal tvål, när man väl tror att man fått tag i den så glider den ur greppet och allt krånglas till. Det kanske även ligger i själva begreppets natur att det försöker beskriva något som vi människor (i alla fall jag) har liten möjlighet att förstå. Det enda man kan göra är att säga att det inte går att verkligen föreställa sig. Vi kan säkert föreställa oss mängden 10 genom att i huvudet rada upp 10 äpplen (eller just din favoritfrukt), lite svårare blir det att föreställa sig 100 äpplen och riktigt svårt när vi närmar oss 1000. Att rada upp oändligt antal äpplen i huvudet är helt enkelt inte rekommenderat och det finns risk för syntax error i våra fina synapser i hjärnan.

Matematikern Dedekind beskrev en oändlig mängd ungefär som att om man tar bort en mängd från denna mängd och den fortfarande är lika stor så är är den oändlig. Det är helt enkelt väldigt svårt för den mänskliga hjärnan att fånga in och bemästra begreppet.

Olika matematikers sätt att beskriva det oändliga

Ovan nämner jag matematikern Dedekinds sätt att beskriva oändlighet men självklart finns det även andra duktiga tänkare som diskuterat (om än något kontroversiellt) begreppet oändlighet. Alltifrån den grekiske matematikern Euklides till mer nutida. Man brukar faktiskt inom matematiken dela upp det här begreppet i två olika typer av oändlighet nämligen potentiell oändlighet och faktisk oändlighet.

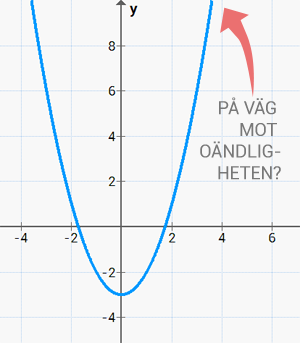Potentiell oändlighet kan sägas vara något som går mot oändligheten (växer) och kan liknas med gränsvärdet oändlighet som vi pratar om när vi beskriver derivata (länk). Du kan exempelvis tänka dig en andragradsfunktion, $ f(x) = x^2 $, som när x växer sig större får ett allt större funktionsvärde. Det här är också något som inte ställer till med någon större diskussion inom matematiken.

Lite mer kontroversiellt har det varit med detsom kallas för faktiskt oändlighet där man menar att oändlighet är en existerande storlek. Det var matematikern Georg Cantor som menade att det gick att beskriva oändligheter som faktiska, och till och med, olika storlekar. Det här har varit ganska kontroversiellt, inte desto mindre då han också hade viss korrespondens med den katolska kyrkan och man anar en viss koppling till det som kallas för gud.

Ett väldigt ändligt slut

Nu är det ändå hög tid att avsluta det här blogginlägget innan vi blir allt för djupa och snöar in på oändliga resonemang, jag hoppas ändå att du som kommit så här långt har fördjupat din syn något på oändligheten och lärt dig något nytt!