Pascals triangel, binom och Sierpinskis triangel
2014-03-12 Av Simon Rybrand 0 kommentarer
I kursen matte 5 på gymnasiet läser man om kombinatorik och binomialsatsen och då stöter man på något som kallas för Pascals triangel. Det här är ett fascinerande sätt att enkelt kunna utveckla så kallade binom (mer om vad det är snart) som har högre grad än 2.
Vem var Pascal?

Räknemaskinen Pascalline skapad av Blaise Pascal
Den som har fått ge namn åt denna triangel, uppbyggd av tal, är den franske matematikern Blaise Pascal som levde på 1600 – talet. Pascal var verksam inte bara inom matematik utan även inom fysik och religion.
Pascal räknas bland annat som den förste att uppfinna en räknemaskin som mekaniskt kunde räkna addition och subtraktion. Hans räknemaskin, som kallades för Pascalline användes bland annat för att förenkla räknearbetet i hans fars affär.
Pascal har även fått ge namn åt den fysikaliska enheten för tryck och åt programmeringsspråket Pascal.
Binom och Pascals triangel
Så vad är då ett binom och pascals triangel?
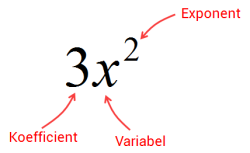
Ett binom är ett algebraiskt uttryck med två stycken termer, exempelvis $(a+b)$ eller $(x^2+2)$. Vanligt är man på gymnasiet övar sig att utveckla sådan uttryck med hjälp av kvadreringsreglerna, exempelvis att $(a+b)^2=a^2+2ab+b^2$ men hur gör man egentligen om man skall utveckla $(a+b)^3$, $(a+b)^4$ eller $(a+b)^8$? Om du själv provar att utveckla dessa uttryck kommer du att märka att det blir en hel del räknearbete. Väldigt mycket och ganska tråkigt räknearbete också.
Om vi ändå skulle göra några av dessa utvecklingar så kan vi se ett mönster som vi kan använda oss av.
$(a+b)^0=1$
$(a+b)^1=a+b$
$(a+b)^2=a^2+2ab+b^2$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$
Om vi här ställer upp koefficienterna i vänsterledet ovanpå varandra så får vi följande:
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1
Här kan vi se att koefficienterna i en utveckling kan tas fram genom att man först sätter ut en etta i början och slutet på nästa rad. Sedan bildas talen mellan dessa genom att addera de två talen ovanför. Exempelvis får vi raden 1 4 6 4 1 genom 1, 1+3, 3+3, 3+1, 1. Om du automatiskt vill hitta fler koefficienterna för högre utvecklingar så kan du använda generatorn här nedan.
Notera även att det finns ett mönster för hur exponenterna utvecklas. Om vi tittar på utvecklingen av
$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$
så kan vi se att exponenten till a minskar för varje term samtidigt som exponenten för b ökar med ett steg för varje term!
Med hjälp av detta kan vi alltså utveckla binom med mycket höga exponenter och ändå göra det på ett snabbare och mer effektivt sätt. Genom att ha en metod så minskar vi även risken att göra enklare räknefel.
Lista fler koefficienter och Rita ut Sierpinski
Här kan du lista fler rader (än ovan nämnda) i pascals triangel. Du kan även färglägga jämna och ojämna tal och därmed få en approximation till Sierpinskis triangel.