Funktionsutmaning
2014-11-07 Av Simon Rybrand 0 kommentarer
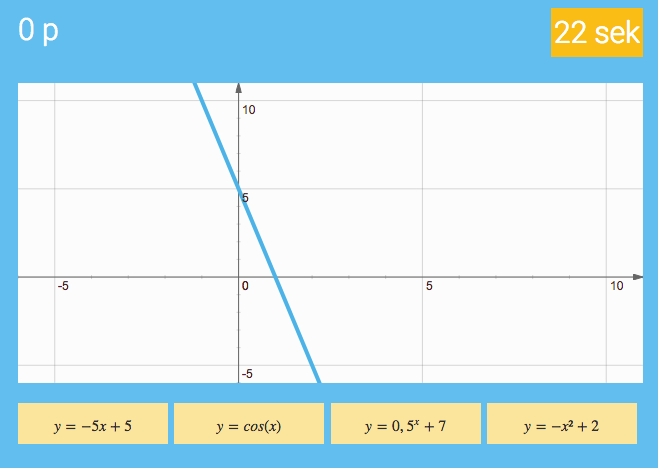
Det är dags för lite spel här på bloggen. Nedanför hittar du ett litet (med betoning på litet) spel där det gäller att gissa vilken funktion som är utritad. Testa gärna så kommer du snabbt förstå hur det fungerar. Kommentera gärna hur många funktioner du lyckas att pricka på 30 sekunder! Det vore också intressant att höra om ni tycker att det är svårt eller lätt.
Spelregler
- Du har 30 sekunder på dig att klicka på rätt funktion och samla så många poäng som möjligt.
- Om du klickar rätt får du en poäng, klickar du fel får du en poäng mindre.
- Lycka till!
Så känner du igen funktionen – Hjälp för att lyckas (bättre)
Det kan förstås vara så att det är ganska svårt att snabbt se vilken typ av funktion som ritas ut på skärmen framför dig. Då kan det vara bra att läsa igenom beskrivningar av de olika funktionerna nedan, för det är väl klart att du vill sätta så hög poäng som möjligt!
Linjära funktioner
Linjära funktioner är funktioner som utritade i en graf är en rät linje. Du känner igen en linjär funktions formel genom att den högsta exponenten till variabeln är 1.
Exempel på linjära funktioner kan vara $y=3x+1$, $y=10$ och $y=2x$. Nedan har vi ritat ut grafen till funktionen $y=3x+1$.
Lär dig mer om räta linjens ekvation och linjära funktioner
Andragradsfunktioner
En andragradsfunktion innehåller variabeln $x^2$ och när de ritas ut kallas de för en parabel. Du kan tänka att de ser ut som en glad eller ledsen mun som är symmetrisk kring en lodrät symmetrilinje. Om formeln har en $+x^2$ term ser grafen ut som en glad mun och om formeln har en $-x^2$ term så ser den ut som en ledsen mun.
Exempel på formler till andragradsfunktioner kan vara $ y=x^2+x $, $y=-3x^2-x+2$ eller $y=x^2+20$. Nedan har vi ritat ut grafen till funktionen $ y=x^2+2{x}-1 $
Exponentialfunktioner
En exponentialfunktion är en funktion där variabeln i funktionsformeln sitter i exponentent. Exempel på sådan funktioner kan vara $ y = 6^x + 2 $ eller $ y = e^{2x} $. Nedan har vi ritat ut två olika typer av sådan funktioner. Dels har vi ritat ut $ y=e^x $ samt $y=10^x$.
Trigonometriska funktioner
Trigonometriska funktioner är funktioner som innehåller de trigonometriska sambanden $sin, cos, tan$. Typiskt för sådan funktioner är att de är periodiska och återkommer till samma värden inom ett visst intervall. Nedan har vi ritat ut grafen till funktionen $y=sinx$.
Övriga
Det finns även lite andra typer av funktioner som kan se ut på andra vis. Nedan visar vi några sådana.
Här är $ y=\frac1x $ utritad.
Här är $ y = \sqrt{x} $ utritad.