Radianer
2012-10-08 Av Simon Rybrand 5 kommentarer
I senare matematikkurser som matematik D och matematik 3 så börjar matteläraren helt plötsligt babbla om ett nytt vinkelmått som kallas radianer inom området trigonometri. I det här blogginlägget tänkte jag att vi skulle definiera det här begreppet och sättet att mäta vinklar så bra så att du sedan själv kan jobba vidare med det. Om du istället föredrar en video om detta så hittar du den här.
Att förstå hur radianer definieras
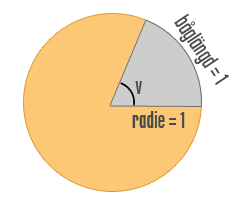
Tänk dig att du har en cirkel med radien 1 l.e (längdenhet) liggande på bordet framför dig. Så tar du fram din tårtspade och och skär ut en tårtbit som har den exakta båglängden 1 (se figur). Vinkeln v som då skapas definieras som 1 rad (rad = radian). Vips så har vi både fått tårta och definitionen av radianer som vinkelmått. När vi har en tårtbit med radien 1 och båglängden 1 så har vi därmed vinkeln 1 rad.

Om vi istället skär ut en tårtbit med båglängden 2 (se figur) så får vi istället vinkeln v 2 radianer.
Om vi nu skulle låta vinkeln gå hela varvet runt på enhetscirkeln så kommer båglängden att bli hela omkretsen på vår cirkel. Så hur stor är egentligen omkretsen på en cirkeln med radien 1 och diametern 2?
Eftersom vi beräknar omkretsen för en cirkel med formeln π*diameter så blir här båglängden = omkretsen π*2 = 2π. Alltså gäller att ett varv har vinkeln 2π rad.
Några vanliga vinkelmått i radianer
- 720˚ = 4π rad
- 360˚ = 2π rad
- 180˚ = π rad
- 90˚ = π/2 rad
- 45˚ = π/4 rad
- 30˚ = π/6 rad
- 1˚ = π/180 rad
Varför skall vi använda radianer istället?
Nu kanske du frågar dig varför du egentligen skall använda radianer istället för grader? Vad är egentligen meningen med det?
finns det lite olika fördelar med detta men framförallt vill vi gå över till vinkelmåttet radianer för att vi skall få en enklare, och snyggare, derivata vi derivering av trigonometriska funktioner. Det visar sig nämligen att när man deriverar trigonometriska funktioner, t.ex. f(x) = cos x och f(x) = sin x, så får vi krångligare uttryck med grader än med radianer.
Från grader till radianer och tillbaka igen
Kanske du nu känner att du både har förstått radianer och vet varför vi egentligen skall använda oss av detta vinkelmått istället och är redo för lite räkneexempel. Låt oss börja att ta några exempel där vi går från grader till radianer och vice versa. Viktigt att känna till när du jobbar med dessa omvandlingar är att 1˚ = π/180 rad.
- 55˚ = 55 * (π/180) = 55π/180 = 11π/36 rad
- 120˚ = 120 * (π/180) = 120π/180 = 2π/3 rad
- π/9 = 180/9 = 20˚
- 2π/5 = 360/5 = 72˚
Träna gärna själv nedan på att göra dessa omvandlingar.
Trigonometriska ekvationer och radianer
Det är framförallt bra att ha koll på att ett helt varv är 2π radianer, ett halvt π radianer och att 90˚ = π/2 radianer när du löser ekvationer och skall svara med radianer i svaret. Det som spelar roll här är att du alltid måste ange periodiciteten för alla lösningar till en ekvation då dessa återkommer om och om igen för sin, cos och tan. Periodiciteten för sin och cos är 360˚ (2π rad) och för tan 90˚ (π/2 rad).
Låt oss ta ett exempel på detta.
Lös ekvationen sin 2x = 0,5
$ sin 2x = 0,5 \Leftrightarrow $
$ 2x = \frac{ pi }{ 6 } + n \cdot 2 \pi \Leftrightarrow $
$ x = \frac{ pi }{ 12 } + n \cdot \pi $
eller
$ 2x = \pi – \frac{ pi }{ 6 } + n \cdot 2 \pi \Leftrightarrow $
$ x = \frac{ 5 pi }{ 12 } + n \cdot pi $
Här kommer ett till inlägg, ursäkta! Ville se om jag är helt ute och cyklar eller om detta möjligtvis kan stämma?
Tack!
sin2x = 0,875 → 0,875 = 7/8
sin2x = 7/8
2x = sin−1 (7/8) + n*2π
2x = 1,065435817 + n2π
2x/ 2 = 1,065435817/ 2 + n2π/ 2
x1 = 0,5327179085 + nπ
________________________________________________
2x = π – 1,065435817 + n2π
2x/ 2 = π/ 2 – 1,065435817/ 2 + n2π/ 2
x2= π/ 2 – 0,5327179085 + n π
Hej
Ser ut som om du är på rätt väg här, du tar med de bägge fallen och gör allt i rätt ordning. De bägge fallen skulle jag kanske skriva som
$ x = \frac{sin^{-1}(\frac78)}{2} + n\pi $
och
$ x = \frac{\pi}{2} – \frac{sin^{-1}(\frac78)}{2} + n\pi $
Det är samma som du har i din lösning.
Hej Simon!
Jag har kört fast på denna fråga:
sin2x=0,875 Svara i radianer.
Har lyckats lösa den så här långt men sen osäker hur jag ska skriva det i radianer..
sin2x=7/8
2x=sin-1(7/8) + n*2π
Tack på förhand!
Ska inte vinkelmåtten vara följande?
720˚ = 4π rad
360˚ = 2π rad
180˚ = π rad
90˚ = π/2 rad
45˚ = π/4 rad
30˚ = π/6 rad
1˚ = π/180 rad
Under rubriken ”Några vanliga vinkelmått i radianer” står det att både 360 och 720 grader är lika med 4π radianer, och att 180 grader är lika med 2π, medan hälften av 180 grader (det vill säga 90 grader) är lika med en fjärdedel av 2π radianer (det vill säga π/2 radianer)
Hej Joel, jo det stämmer att det står fel i listan där, det är uppdaterat. Tack för att du tog dig tid och påpekade detta!