Det gyllene snittet, konst och matematik
2014-04-08 Av Simon Rybrand 4 kommentarer
Vad är det som gör att vi upplever något som vackert, harmoniskt eller proportionerligt? Man brukar ju säga att smaken är som baken (delad) men i många fall så upplever vi människor vissa saker som vackra eller inte.
I det här blogginlägget tänkte jag att vi skulle titta på ett förhållande som kallas för gyllene snittet som är ett alldeles speciellt förhållande mellan längder. Det är nämligen så att detta återkommer om och om igen i naturen och vi människor ofta upplever det som vackert. Vi skall börja med att försöka återskapa detta förhållande med passare och linjal fast i digital form.
Varför uppskattar vi det gyllene snittet och hur används det?
Om vi skulle filosofera lite (gissa) kring varför det gyllene snittet upplevs som vackert så kan det bero på att det faktiskt återkommer i naturen på många olika vis. Det här påverkar såklart oss människor. Du kan hitta det gyllene snittet i alltifrån grankottar, fibonaccis talföljd, tavlor till hur solrosor ser ut så säkerligen har vi människor påverkats av detta.
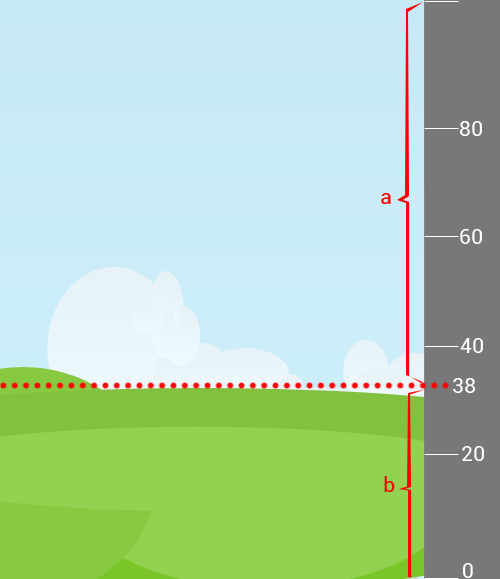
 Låt säga att vi skall måla ett landskapsmotiv och vill använda oss av att det gyllene snittet ofta upplevs som vackert om vi placerar horisonten efter detta då tavlan är 1 meter hög (vi målar ett stående motiv). Vi kan då använda oss av att vet att gyllene snittet är cirka 1.618 för att placera ut horisonten ungefär rätt.
Låt säga att vi skall måla ett landskapsmotiv och vill använda oss av att det gyllene snittet ofta upplevs som vackert om vi placerar horisonten efter detta då tavlan är 1 meter hög (vi målar ett stående motiv). Vi kan då använda oss av att vet att gyllene snittet är cirka 1.618 för att placera ut horisonten ungefär rätt.
Så om vi tänker oss att a/b = 1,618 så ger det oss att a = 1,618⋅b. Eftersom att tavlan är 1 meter hög så vet vi att
$ 1,618b + b = 1 ⇔ b = 0,38 $
Dvs vi drar vårt röda gyllene streck på höjden (ungefär) 38 cm och ritar vårt landskap under detta. Förhoppningsvis kommer då våra utställningsbesökare att uppskatta tavlan och vi säljer den kanske dyrt ;-).
Hur definieras det gyllene snittet?
Det kan också vara intressant att gå in på hur det gyllene snittet kan tas fram mer exakt. För detta så måste vi gå till definitionen av gyllene snittet:
När en sträcka delas i en längre del a och en kortare del b så är det gyllene snittet när förhållandet mellan a och b är samma som förhållandet mellan a+b till a. Dvs att
$ \text{Gyllene snittet} = \varphi = \frac{a+b}{a}=\frac{a}{b} $
Vi gör så att vi sätter $ \text{Gyllene Snittet} = \varphi $ och vi vet att
1) $ \varphi = \frac{a+b}{a} $
2) $ \varphi = \frac{a}{b} $
Vi delar alla delar i 1) med b och får då
Från 2) vet vi att $ \varphi = \frac{a}{b} $. Vi byter därför ut $\frac{a}{b}$ mot $\varphi$ så att vi får att
$\frac{\frac{a}{b}+1}{\frac{a}{b}} = \frac{\varphi+1}{\varphi} $
Detta skall vara lika med det gyllene snittet $ \varphi $ så vi får därmed följande ekvation:
$ \frac{\varphi+1}{\varphi} = \varphi ⇔ $ (Förläng med $ \varphi $)
$ \varphi+1 = \varphi^2 ⇔ $ (Flytta över till en sida om likhetstecknet)
$ \varphi^2-\varphi-1 = 0 ⇔ $
Här kan vi används oss av pq-formeln för att lösa ut $ \varphi $ men vi tar bara med den positiva lösningen då det är geometriska avstånd som avses:
$ \varphi = \frac{1}{2} + \sqrt{\frac{1}{4}+1} ⇔ $
$ \varphi = \frac{1}{2} + \sqrt{\frac{5}{4}} ⇔ $
$ \varphi = \frac{1}{2} + \frac{\sqrt{5}}{2} ⇔ $
$ \varphi = \frac{1+\sqrt{5}}{2} $
Nu har vi det gyllene snittet:
$ \varphi = \frac{1+\sqrt{5}}{2} ≈ 1.61803398874989 $
Hej,
Vad spännande!
Jag är bildlärare och tänker testa era beräkningar i mina elevers arbeten (landskap).
Hur jag kom hit att läsa om det, undrar man?
Jo, jag börjat spinna från historien om Apple- logotyp, då jag ville inspirera eleverna med det fascinerande betydelse av en så vardaglig frukt som äpple, efter vi både ritat och målat det under några lektioner… 🙂 Tack för en vetenskaplig inspiration!
Hälsningar från Loviselundsskolan, Sthlm .
Kul.
Lycka till!
Tack! Har funderat på hur jag kan använda detta på olika sätt under en tid, men inte tagit tag i att ta reda på mer. Detta var bra förklarat.
Mvh Katarina Björklund
Kul att du tyckte att det var bra förklarat och att vi kan vara till hjälp!