5 Matteskämt du faktiskt lär dig något av

2015-05-05 Av Simon Rybrand 10 kommentarer

Det finns enligt min mening två problem med matematikskämt. Det första problemet är man ofta måste kunna en hel del matematik för att förstå skämten. Det finns många matematikskämt som man behöver en förklaring på och skämt som kräver en djupare förklaring blir sällan särskilt roliga. Det andra problemet är att dessa typer av skämt tenderar att bli en aning “torra” och teoretiska.

Men inte desto mindre så kan dessa typer av nördiga skämt ibland glimra till och vara roliga, på riktigt. Dessutom kan du faktiskt lära dig en hel del av dessa typer av skämt, och ju mer du lär dig desto roligare blir de.

Listan – 5 Matteskämt du faktiskt lär dig något av

Här har vi gjort så att vi har samlat 5 matteskämt som vi tycker både är roliga (oftast) och du lär dig något av. Till varje skämt har vi även tagit med en förklaring av teorin bakom och självklart länkar till videos som förklarar begreppen i skämtet. Och om du har ett eget matematikskämt på lager så kommentera gärna!

1. Den kalla mängden…

”Vet du varför det är så kallt i tomma mängden?
– För att det inte finns några element där.”

Förklaring

Här är ett skämt om mängdlära, som finns i matematik 5, där man behöver förstå att en mängd består av ett antal element. I den tomma mängden $∅$ finns det inga element vilket gör att det blir väldigt kallt. Se en video om delmängder här.

2. Ordkrig mellan tal

Förklaring

Det här skämtet, i form av en bild, blir bäst på engelska. Det är alltså talet π som säger till ett imaginärt tal i att ”get real” (betyder ungefär skärp till dig) och det imaginära talet i säger till π att ”be rational” (betyder ungefär ”var lite realistisk”). Det här skämtet syftar på de olika grupper av tal som finns, tex naturliga tal, hela tal, rationella tal, reella tal och komplexa tal. Se en video om tal och talmängder här.

3. Livsfarlig derivata

De två funktionerna $x$ och $e^x$ var ute och gick då de helt plötsligt fick syn på en derivataoperator.

Funktionen $x$ blev då jätterädd att den skulle bli deriverad och bara bli 1, eller ännu värre inte bli någonting och dö om den blev utsatt flera gånger för derivataoperatorn.

När $x$ ville gå, sa $e^x$ kaxigt, jag går fram och gör upp. Han kan derivera mig hur många gånger som helst utan att det gör något, jag förblir densamme.

När $e^x$ kommer fram är det sista han hör. Det är jag som är $\frac{dy}{dt}$.

Förklaring

Här är det några saker som man behöver ha koll på för att förstå skämtet:

• Dels kan det vara bra att förstå begreppet derivata, deriveringsregler och hur man deriverar exponentialfunktioner. Derivatan av $x$ är $1$ och deriverar man en konstant $1$ så blir derivatan $0$. Det speciella med derivatan av funktionen $e^x$ är att derivatan är samma, dvs $e^x$.
• Derivata skrivs ofta som $f'(x)$ eller $y’$ men vi kan också skriva $\frac{dy}{dx}$ vilket sägas som ”derivatan av funktionen y med avseende på variabeln x”.
• Om vi därför deriverar med avseende på variabeln t, $\frac{dy}{dt}$, så ses varabeln x som en konstant och därmed är $e^x$ en konstant vars derivata är 0. Och där har du förklaringen till skämtets poäng.

 4. Välsmakande matematik

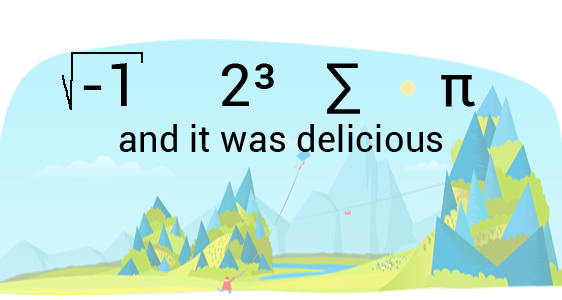
Förklaring

Den här bilden måste tolkas på engelska för att vi skall förstå den. Det är som en rebus som skall tolkas som ”I ate some pie”, förklaringen till det är följande.

• $\sqrt{-1} = i$, se video om komplexa tal och imaginära tal
• $2^3=8$ som uttalas ”ate” på engelska.
• $∑$ är ett summatecken eller ”sum” på engelska som uttalas ”some”.
• $\pi$ dvs ”pie” (som i paj fast på engelska)

5. Konstiga gränsvärden

Förklaring

Här har eleven missförstått gränsvärden en hel del. Eleven tolkar det som att man skall vända ”åttan” istället för att gränsvärdet går mot oändligheten ∞. Därför vänder denne elev bara på ”femman”. Här behöver man förstå att när nämnaren går mot 0 så kommer hela uttrycket gå mot oändligheten.

Ett extra matteskämt utan förklaring….

 ”Det finns bara 10 sorters personer i världen, de som förstår binära tal och de som inte gör det”

Här lämnar jag till läsaren att förstå skämtet, kommentera gärna om du kommer på det. Ett tips finns ändå här.