Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
- Vad är ett gränsvärde?
- Skrivsättet limes i matematiken
- Att beräkna gränsvärden algebraiskt
- Gränsvärden då $x$x går mot $a$a
- Gränsvärden då $x$x går mot oändligheten
- Gränsvärdet är oegentligt eller saknas
- Att bestämma gränsvärden grafiskt
- Räkneregel för gränsvärden
- Att beräkna gränsvärden numeriskt
- När använder man gränsvärden?
- Utvidgad kontinuitet
- Exempel i videon
- Kommentarer
Vad är ett gränsvärde?
Att undersöka gränsvärden till funktioner, innebär att undersöka vad som händer med funktionsvärdet då variabeln, ofta xx, närmar sig ett givet värde.
Vi kan inte beräkna funktionsvärdet för f(x)=ƒ (x)= x−3x2−6x+9x2−6x+9x−3 för x=3x=3 genom insättning. För när x=3x=3 blir nämnaren lika med noll och vi får en kvot vi inte kan beräkna värdet av. Det leder till att funktionen inte är definierar för detta värde.
Däremot kan vi bestämma värdet på kvoten för xx -värden som ligger väldigt nära 33, tex x=2,9999x=2,9999 eller x=3,0001x=3,0001. Genom att bestämma kvotens värde för xx-värden oändligt nära ett värde som inte ingår i definitionsmängden kan vi beräkna ett gränsvärde.
Ett gränsvärde är det värde uttrycket eller funktionen antar, när variabeln närmar sig det värde variabeln ”går mot”.
Skrivsättet limes i matematiken
Gränsvärden betecknas med lim efter latinskans limes. För att ange att ”x går mot a” skriver man x→a.
För att skriva ” fƒ går mot gränsvärdet LL när x går mot a” använder man skrivsätten
x→alimf=L
eller
f→Lƒ →L när x→ax→a .
Man kan förstå uttrycket ”går mot” som att xx -värdet närmar sig det värde det ”går mot” otroligt mycket. Så mycket att man till och med kan ersätta variabeln med värdet vid beräkningen av uttryckets gränsvärde.
Att beräkna gränsvärden algebraiskt
Du beräknar ett gränsvärde genom att ersätta variabeln med det givna värdet det går mot, för att sedan beräkna uttryckets eller funktionens värde.

För vissa uttryck och funktioner kan man beräkna gränsvärdet direkt genom insättning. För andra behöver man först förenkla eller skriva om uttrycket på olika vis, för att sedan kunna beräkna gränsvärdet.
Gränsvärden då xx går mot aa
Vi har två olika typer av gränsvärden.
Ett då variabeln xx närmar sig en punkt x=ax=a. Med matematiska symboler skriver gränsvärdet så här.
x→alimf(x)=A
Det utläses ”gränsvärdet då xx går mot noll för funktionen fƒ av xx är lika med A.”
För att kunna bestämma gränsvärden då x→ax→a måste funktionen fƒ vara definierad för värden väldigt nära aa, om än ej i själva punkten. Vi tar ett exempel.
Exempel 1
Beräkna gränsvärdet x→3lim 4+x4+x
Lösning
Genom att låta xx närma sig värdet 33 kommer uttrycket närma sig värdet 77, därför att
x→3lim 4+x=4+x= 4+3=74+3=7
Här var det det inget problem att låta variabeln gå mot värdet utan att skriva om eller förenkla först. Men det är inte alltid så lätt.
Exempel 2
Beräkna gränsvärdet h→0lim h3h+h23h+h2h
Lösning
Ersätter vi hh med noll direkt, får vi en nolldivision, alltså en kvot där nämnaren är noll. Då kan vi inte beräkna kvotens värde och därmed inte gränsvärdet. Därför förenklar vi först uttrycket till
h3h+h2=hh(3+h)=13+h=3h+h2h =h(3+h)h =3+h1 = 3+h3+h
Nu beräknar vi gränsvärdet genom att ersätta hh med noll.
h→0lim (3+h)=3+0=3(3+h)=3+0=3
Gränsvärden då xx går mot oändligheten
Den andra gränsvärdestypen är den då variabeln xx närmar sig väldigt stora positiva eller negativ tal. Med matematiska symboler skriver vi det gränsvärdet så här.
x→∞limf(x)=A
x→−∞limf(x)=A
Det utläses ”gränsvärdet då xx går mot positiva/negativa oändligheten för funktionen fƒ av xx är lika med A.”
Skrivsättet ∞ motsvarar underförstått +∞.
Exempel 3
Beräkna gränsvärdet x →∞lim x4+4x +66
Lösning
Genom att låta xx närma sig oändligt stora positiva värden kommer uttrycket närma sig värdet 66, därför att
x→∞lim x4+4x + 6=0+6=66=0+6=6
Sammanfattningsvis lägger vi till följande definition.
Gränsvärde
För alla kontinuerlig funktioner gäller att
x→alimf(x)=f(a)
Här ovan står alltså, att gränsvärdet för funktionen f(x) då vi låter x-värdet gå mot a, är lika med funktionsvärdet f(a)ƒ (a).
Gränsvärdet är oegentligt eller saknas
När vi beräknar gränsvärden kommer vi upptäcka att vi inte alltid får fram ett entydigt gränsvärde. Exempelvis är inte kvoterna ∞kk∞ där kk är en konstant eller ∞∞∞∞ definierade. Inte heller produkten k⋅∞k·∞ eller nolldivision, alltså kvoter där nämnaren är lika med noll.
För att kunna avgöra om gränsvärdet är oegentligt eller saknas behöver vi studera funktionen närmre.
I de fall då gränsvärdet går mot positiva eller negativa oändligheten, ±∞±∞, för x=ax=a, säger man att vi har ett oegentligt gränsvärde. Det vill säga, vi kan inte ange ett specifikt numeriskt värde.
När man ska förenkla rationella funktionsuttryck för att beräkna gränsvärden då x→∞x→∞ är en effektiv metod att bryta ut, eller förkorta med, den dominerande faktorn i täljaren och nämnare, alltså faktorn med högst grad.
Exempel 4
Beräkna gränsvärdet x →∞lim 2x2−54x3−3x4x3−3x2x2−5
Lösning
Genom att direkt ersätta xx med oändligheten ger ∞∞∞∞ vilket inte är definierat. Även om vi förkortar uttrycket får vi att
x →∞lim 2x2−54x3−3x=4x3−3x2x2−5 =
x →∞lim x2x3⋅2−x254−x23=x3x2 ·4−3x2 2−5x2 =
x →∞lim x⋅x·2−x254−x23=4−3x2 2−5x2 =
∞⋅2+04+0=∞⋅2∞·4+02+0 =∞·2
som inte är definierat som ett gränsvärde och vi säger att gränsvärdet är oegentligt.
Vi säger även att gränsvärdet saknas då det inte närmar sig samma funktionsvärdevärde om vi närmar oss x=ax=a från höger eller vänster.
Det andra fallet inträffar när en funktion går mot olika yy-värden för samma xx-värde. Man kan dra denna slutsats både utifrån algebraiska beräkningar och grafiska studier. Grafiskt ser vi att gränsvärden saknas i punkten x=ax=a när grafen inte ger samma gränsvärde om man närmar sig punkten från höger eller vänster.
Att bestämma gränsvärden grafiskt
Ett alternativ till att bestämma gränsvärdet algebraiskt är att skissa grafen. Vi undersöker gränsvärdet grafiskt.
Exempel 5
Avgör om gränsvärdet existerar för f(x)=ƒ (x)= x311x3 +2+2 genom att rita grafen till funktionen.
a) x →0limf(x)
b) x →∞limf(x)
Lösning
Vi ritar grafen.
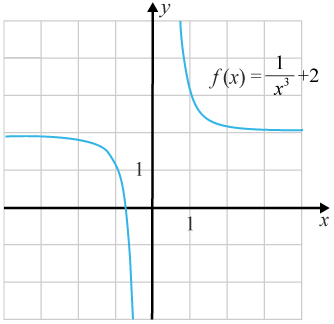
a) Då x →−0limf(x)=−∞ och x →+0limf(x)=+∞ är gränsvärdet inte det samma från höger och vänster och existerar därmed inte. Vi säger att gränsvärdet saknas.
b) Vi ser att grafen närmar sig yy-värdet 22 då xx går mot oändligheten och vi får därmed att gränsvärdet existerar. Vi får att x →∞limf(x)=2
Räkneregel för gränsvärden
Vi uppmärksamma följande räkneregel för gränsvärden, vilken kan bli användbar när vi längre fram ska ta fram ett antal deriveringsregler.
x→alim(f(x)+g(x))=x→alimf(x)+x→alimg(x)
Vi tittar på ett exempel på detta.
Exempel 6
Beräkna gränsvärdet x →3lim x6+68x6x +8x6
Lösning
Vi delar upp uttrycket i två funktionsuttryck där f(x)=ƒ (x)= x66x och g(x)=g(x)= 68x8x6 och beräknar gränsvärdena var för sig.
x→3limf(x)=x→3lim x6=366x =63 =2=2
och
x→3limg(x)=x→3lim 68⋅3=6248·36 =246 =4=4
vilket ger att
x→3lim(f(x)+g(x))=2+4=62+4=6
Att beräkna gränsvärden numeriskt
För vissa funktioner är det inte möjligt att beräkna gränsvärdet algebraiskt. Då kan man försöka bestämma gränsvärdet genom att sätta värden nära värdet variabeln går mot för att på så sätt beräkna ett gränsvärdet numeriskt.
Exempel 7
Grafen beskriver exponentialfunktionen y=−0,7x+5y=−0,7x+5. Bestäm funktionens gränsvärde då xx blir oändligt stort.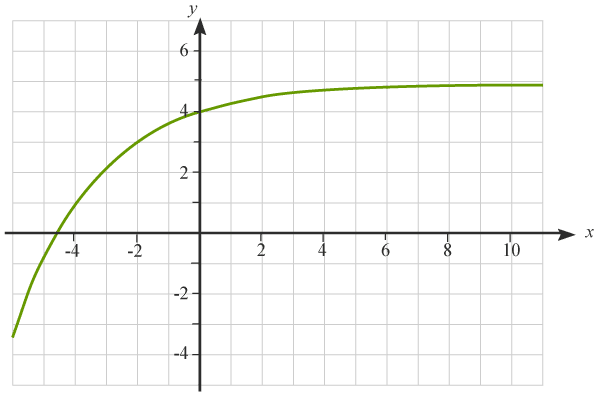
Lösning
Genom att studera grafen ser vi att funktionen närmar sig värdet y=5y=5 då funktionen antar större och större värde på xx .
Algebraiskt kan vi beräkna detta genom att större och större värden för xx.
x=10x=10 ⇒ y(10)=−0,710+5≈−2,8⋅10−1+5=4,72y(10)=−0,710+5≈−2,8·10−1+5=4,72
x=100x=100 ⇒ y(100)=−0,7100+5≈−3,23⋅1016+5≈0+5=5y(100)=−0,7100+5≈−3,23·1016+5≈0+5=5
x=1 000 ⇒ y(1 000)=−0,71 000+5≈−1,25⋅10−155+5≈0+5=5y(1 000)=−0,71 000+5≈−1,25·10−155+5≈0+5=5
x=1 000 000 ⇒ y(1 000 000)=−0,71 000 000+5≈−1,10⋅10−154 902+5≈0+5=5y(1 000 000)=−0,71 000 000+5≈−1,10·10−154 902+5≈0+5=5
Vi ser att för x=1 000 000x=1 000 000 får y(1 000 000)=−0,71 000 000+5≈0+5=5y(1 000 000)=−0,71 000 000+5≈0+5=5.
Det innebär att gränsvärdet för funktionen när xx blir oändligt stort är 55.
Med ett matematiskt språk skriver vi
x→∞lim −0,7x+5=0+5=5−0,7x+5=0+5=5
Man skulle även resonera sig fram till svaret genom att veta att en bas som finns i intervallet 0<0< a<1a<1 kommer bli mindre och mindre ju större exponenten blir. Tillslut kommer värdet vara så litet att man kan räkna med det som det som värdet noll.
När använder man gränsvärden?
När vi vill beskriva hur en funktion förändras beräknar vi en ändringskvot i ett intervall. Ju mindre intervall vi väljer, ju bättre närmevärde till funktionens faktiska förändringshastighet. Vill vi få en exakt beskrivning av förändringen i en punkt behöver vi en tangent istället. Alltså en linje som tangerar, ”rör vid”, grafen i endast en punkt.
Men en tangent är inte helt lätta att rita så att den får en korrekt lutning, en lutning som faktiskt motsvarar punktens lutning. Lättare då är att rita en sekant, med ett mycket litet avstånd mellan de två punkterna. Det är här gränsvärdet framför allt tillämpas i denna kurs. Vi vill göra så att avståndet mellan punkterna närmar sig värdet noll. Alltså sammanfaller och går från att vara två punkter till att bli en. Det är detta gränsvärde som vi ska använda för att definiera derivatan.
En annan tillämpning är, som vi nämnt tidigare i denna text, för att kunna beräkna funktionens närmevärde för i punkter på grafen som ligger mycket nära variabelvärden där funktionen annars inte är definierad. Till exempel för rationella funktioner. För att kunna motivera kontinuitet hos en rationell funktion kan vi använda gränsvärdet gör att utvidga den.
Utvidgad kontinuitet
För den som vill gräva ännu djupare inom begreppet gränsvärde ska vi nu titta på ett exempel på hur vi kan utvidga kontinuiteten med hjälp av gränsvärdet. Vi har tidigare sagt att ett gränsvärde existerar då x→ax→a och funktionen f är definierad för värden väldigt nära a.
Exempel 8
Undersök om den rationella funktionen f(x)= x2−5xx2−6xx2−6xx2−5x är kontinuerlig i punkterna x=0 och x=5.
Lösning
En funktionen är kontinuerligt om den är kontinuerlig i hela sin definitionsmängd.
Vi ser att vi får nolldivision för x=0x=0 och x=5x=5 vilket ger att det rationella uttrycket inte är definierat för dessa värden. Men hur är det med den rationella funktionen?
Vi undersöker om vi kan utvidga definitionsmängden för den rationella funktionen med hjälp av gränsvärdena då x→0 och x→5.
Vi beräknar gränsvärdet för x→0 och får att
x→0limf(x)= x2−5xx2−6x=x2−6xx2−5x =x→5limf(x)= x(x−5)x(x−6)=x(x−6)x(x−5) =x→0limf(x)= x−5x−6=x−6x−5 = −5−6=−6−5 = 1,21,2
vilket ger att gränsvärdet existerar och vi kan utvidga definitions och värdemängden med hjälp av gränsvärdet f(0)=1,2ƒ (0)=1,2.
Däremot kan vi inte definiera f(5) eftersom att x→5limf(x) inte existerar. Vi kan avgöra detta grafiskt genom att skissa grafen till den rationella funktionen.
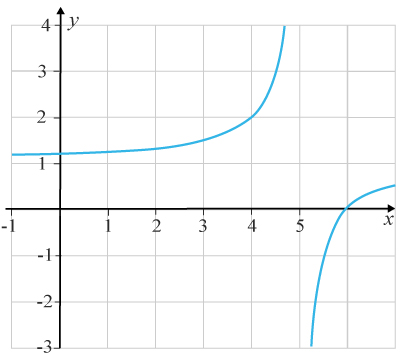
Vi ser att då vi närmar oss x=5x=5 från vänster gäller att
x→5−limf(x) går mot oändligt stora positiva funktionsvärden
och då vi närmar oss x=5x=5 från höger ger att
x→5+limf(x) går mot oändligt stora negativ funktionsvärden
vilket leder till att
x→5+limf(x)=x→5−limf(x)
och vi saknar därmed ett gränsvärde då xx går mot 55.
Den rationella funktionen fƒ är kontinuerlig. Och med hjälp av gränsvärdet kan vi även lägga till x=0 i definitionsmängden så att fƒ blir kontinuerlig även för x=0x=0. Men inte x=5 då gränsvärdet x→5limf(x) inte existerar.
Exempel i videon
- Beräkna gränsvärdet x→∞limx1
- Beräkna gränsvärdet x→10lim(100+x)
- Beräkna gränsvärdet h→0limh2hx+h2
- Beräkna gränsvärdet x→∞lim(9+x9)
Kommentarer
e-uppgifter (11)
1.
(1/0/0)E C A B P 1 PL M R K Beräkna gränsvärdet x→5lim ( 7+x)( 7+x)
Svar:Ditt svar:Rätt svar: 12(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B P 1 PL M R K Beräkna gränsvärdet h→2lim (3h+1000)(3h+1000)
Svar:Ditt svar:Rätt svar: 1006(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K Bestäm x→3lim x1212x
Svar:Ditt svar:Rätt svar: 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B P 1 PL M R K Beräkna gränsvärdet x→0lim 30+x151530+x
Svar:Ditt svar:Rätt svar: 21(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm x→−4lim20+x
Svar:Ditt svar:Rätt svar: 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B P 1 PL M R K Beräkna gränsvärdet x→8lim ( x2)( x2)
Svar:Ditt svar:Rätt svar: 64(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(1/0/0)E C A B P 1 PL M R K Beräkna gränsvärdet x→2lim (20x+x2+10)(20x+x2+10)
Svar:Ditt svar:Rätt svar: 54 då x→2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(1/0/0)E C A B 1 P PL M R K Bestäm x→9lim (x+1)(√x+1)
Svar:Ditt svar:Rätt svar: 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: GränsvärdenRättar...9. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm h→∞lim (10−h100)(10−100h )
Svar:Ditt svar:Rätt svar: 10(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(1/0/0)E C A B 1 P PL M R K Grafen visar funktionen f(x)=ƒ (x)= x11x +5+5 .
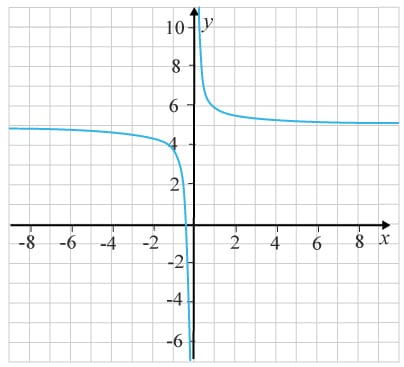
Ange gränsvärdet för funktionen f(x)ƒ (x) då x→±∞x→±∞
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...11. Premium
(1/0/0)E C A B 1 P PL M R K Bestäm x→0lim(4⋅ex+3)
Svar:Ditt svar:Rätt svar: 7(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (11)
12. Premium
(0/2/0)E C A B P 1 PL M R 1 K Beräkna gränsvärdet x→∞lim x+22020x+2
Svar:Ditt svar:Rätt svar: 0(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...13. Premium
(0/2/0)E C A B P 1 PL M R 1 K Figuren illustrerar grafen för f(x)=ƒ (x)=x−511x−5 .
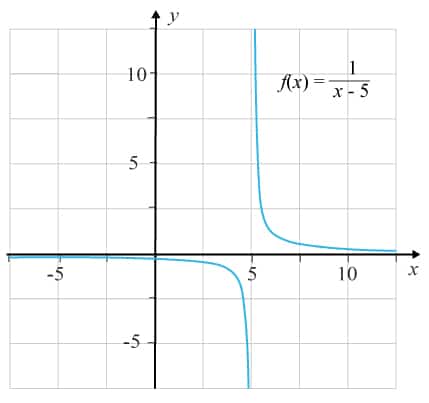
Ange gränsvärdet för funktionen f(x)ƒ (x) då x→5x→5.
Träna även på att motivera ditt svar.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...14. Premium
(0/1/0)ME C A B 1 P PL M R K Beräkna om möjligt gränsvärdet x→0−lim x11x
Svar:Ditt svar:Rätt svar: Gränsvärdet är oegentligt då funktionsvärdet går mot den negativa oändligheten när x går mot noll fårn vänster.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...15. Premium
(0/1/0)E C A B P 1 PL M R K Beräkna gränsvärdet h→0lim h10x3h−h210x3h−h2h
Svar:Ditt svar:Rätt svar: 10x3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...16. Premium
(0/2/0)E C A B 1 P 1 PL M R K Bestäm x→0lim 4x28x3+16x28x3+16x24x2
Svar:Ditt svar:Rätt svar: 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: GränsvärdenRättar...17. Premium
(0/2/0)E C A B 1 P 1 PL M R K Bestäm x→0lim x2+3xxxx2+3x
Svar:Ditt svar:Rätt svar: 31(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...18. Premium
(0/2/0)E C A B 1 P 1 PL M R K Bestäm x→∞lim 4x2x+62x+64x
Svar:Ditt svar:Rätt svar: 21(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...19. Premium
(0/1/0)E C A B 1 P PL M R K Bestäm x→∞lim(8⋅0,2x+9)
Svar:Ditt svar:Rätt svar: 9(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...20. Premium
(0/1/0)ME C A B P PL M R 1 K Rita grafen till f(x)=ƒ (x)=x211x2 .
Bestäm gränsvärdet x→0lim f(x)ƒ (x)
Svar:Ditt svar:Rätt svar: Gränsvärdet är oegentligt.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...21. Premium
(0/2/0)ME C A B 1 P PL M R 1 K Rita grafen till f(x)=ƒ (x)=x2−6x+9x2−3xx2−3xx2−6x+9 .
Bestäm gränsvärdet x→3lim f(x)ƒ (x).
Svar:Ditt svar:Rätt svar: Gränsvärde saknas.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...22. Premium
(0/3/0)E C A B 1 P 1 PL M R K 1 Vill man ange ett troligt gränsvärde på en funktion som inte kan förenklas algebraiskt, får man beräkna ett troligt gränsvärde genom upprepade beräkningar för mindre och mindre värden.
Bestäm ett troligt gränsvärde för h→0lim h103+h−103103+h−103h med en decimals säkerhet.
Svar:Ditt svar:Rätt svar: 2302,6 då h→0(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (7)
23. Premium
(1/0/1)M NPE C A B 1 P PL 1 M R K Bestäm
a) x→0lim(ex+7)
b) x→∞ lim 4x+916x√16x4x+9
Svar:Ditt svar:Rätt svar: a) 8 b) 2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...24. Premium
(0/0/1)E C A B P 1 PL M R K Beräkna gränsvärdet x →∞lim 2x2−54x2−3x4x2−3x2x2−5
Svar:Ditt svar:Rätt svar: Gränsvärdet är 2 då x→∞(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...25. Premium
(0/0/1)E C A B P 1 PL M R K Bestäm gränsvärdet x →∞lim CaxCax då C>0C>0 och 0<0<a<1a<1
Svar:Ditt svar:Rätt svar: 0(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...26. Premium
(0/0/1)ME C A B P 1 PL M R K Bestäm gränsvärdet x →∞lim CaxCax då C>0C>0 och a>1a>1
Svar:Ditt svar:Rätt svar: Gärnsvärdet är oegentligt.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...27. Premium
(0/0/1)E C A B P PL 1 M R K Bestämx→∞ lim 2x+132x√32x2x+1
Svar:Ditt svar:Rätt svar: Gränsvärdet är 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: GränsvärdenRättar...28. Premium
(0/0/3)M NPE C A B P PL 1 M R 1 K 1 Bestäm konstanten AA så att x→∞lim4x+AAx=71Ax4x+A =17
Svar:Ditt svar:Rätt svar: A=74(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: GränsvärdenRättar...29. Premium
(0/0/1)E C A B P PL 1 M R K Bestäm x→∞lim 3xx3x33x
Svar:Ditt svar:Rätt svar: 0(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Douglas Berg
I förklaringen får vi nollvision, men det är väll nolldivision vi är ute efter?
Anna Eddler Redaktör (Moderator)
Hej Douglas,
vi får aldrig dividera med noll. Därför skriver vi först om uttrycket enligt förklaringen och sätter där efter in x=0 får att beräkna uttryckets värde. Och då har vi inte längre nolldivision.
Rasmus Mononen
I sista uppgiften dyker det i förklaringen upp en 3:a i nämnaren när ”h” ersätts med olika tal. 3:an finns inte med i grunduttrycket. Kunde inte lösa uppgiften – men nu när 3:an dök upp så är det ju möjligt. Borde 3:an stå med från början? // Rasmus
David Admin (Moderator)
Hej Rasmus.
I uppgiften har du trean i exponenten. Det är därifrån trean kommer.
h→0limh103+h−103
Du sätter sedan in små värden för h och beräknar.
Anna Nyback
hej! Skulle behöva hjälp med att lösa denna uppgift:
lim x->∞ 4x^2+3x-5/x^2+1
Tacksam för hjälp!
Simon Rybrand (Moderator)
Är det uttrycket x2+14x2+3x−5?
Tobias Persson
Ljudet på denna videon funkar inte
Simon Rybrand (Moderator)
Testade snabbt här och då fungerade det. Vilken webbläsare/datortyp/mobil använder du?
Mattefreak
Blir inte riktigt klok på
lim —> oändligheten 2x/x^2
Försöker bestämma gränsvärdet, men fastar på denna
Simon Rybrand (Moderator)
x→∞limx22x
Förkorta med x
x→∞limx2=0
Tim Fredell
Sitter med samma uppgift som jag antar att Kim Kärki, några poster upp, tidigare försökte förklara.
x→2lim(x−2x2−4+x2−44x−8)
Skulle uppskatta hjälp på denna uppgift.
Simon Rybrand (Moderator)
Hej! Det blir enklare här att se vad gränsvärdet går mot om vi först förenklar det rationella uttrycken.
Det första vi kan göra är att med hjälp av konjugatregeln skriva x2−4=x2−22=(x+2)(x−2). Då får vi
x−2(x+2)(x−2)+(x+2)(x−2)4x−8
I den andra termens täljare bryter vi nu ut 4 och får
x−2(x+2)(x−2)+(x+2)(x−2)4(x−2)
I bägge termerna kan vi nu förkorta med (x−2) vilket ger oss
x+2+x+24
Så nu har vi gränsvärdet
x→2lim(x+2+x+24)=5
då
2+2+2+24=4+1=5
Kim kärki
Hej, hur löser jag denna gränsvärde lim x^2+10x+25/x+5 (x går mot -5)
Simon Rybrand (Moderator)
Faktorisera täljaren med en kvadreringsregel så att du får
x2+10x+25=(x+5)2
Då får du gränsvärdet
x→−5limx+5(x+5)2=
x→−5lim(x+5)=0
Anton Boyertson
Hej
I uppgift 3 så sår det: lim x→0 i 1/x och svaret ska vara −∞ men om man testar att räkna ut några steg på vägen t.ex. 1/0.1=10 1/0.01=100 1/0.001=1000 så värkar det för mig som om det går mot den positiva oändligheten, skulle du kunna förklara hur jag tänker fel och hur jag ska tänka.
Tack
Simon Rybrand (Moderator)
Hej Anton
Här står det att x går mot ”minus noll”, dvs x→0−. Det här innebär att vi går mot 0 från vänster så det du skall skriva istället är:
1/-0.1=-10 1/-0.01=-100 1/-0.001=-1000
Ett gränsvärde kan närma sig något både från vänster och från höger.
Kim kärki
Hur löser jag följande: lim —>2 (x^2-4/x-2+4x-8/x^2-4) ?
Simon Rybrand (Moderator)
Stämmer det att det gäller uttrycket x→2lim(x2−x4−2+4x−x28−4)?
I så fall går det gränsvärdet mot 2 då
22−24−2+4⋅2−228−4=2
OliviaFrida
Hej!
Hur räknar man ut lim t->0 för t / (roten ur 4+t minus roten ur 4-t)
Simon Rybrand (Moderator)
Antar att du menar gränsvärdet
t→0lim4+t−4−tt
Här kan du multiplicera med nämnarens konjugat både i täljaren och nämnaren, dvs
(4+t−4−t)(4+t+4−t)t(4+t+4−t)
Nu kan du utveckla nämnaren med konjugatregeln och då ges
(4+t)2−(4−t)2t(4+t+4−t)= 4+t−(4−t)t(4+t+4−t)=
2tt(4+t+4−t)= 21(4+t+4−t)
Om du nu låter t gå mot noll i detta uttryck så kommer du få gränsvärdet 2. Dvs
t→0lim4+t−4−tt=2
Cissi
Ja på första skulle det vara f(x)=(x-2)^2/(x-2)
Cissi
eller nej utan parentes i nämnaren, i övrigt samma
Simon Rybrand (Moderator)
x−2(x−2)2=x−2
så
x→2lim(x−2)=0
Cissi
Hej, jag har en fråga om två tal. Vad blir gränsvärdet (om det finns nåt) i de här talen då x närmar sig 2?
f(x)= (2-2)^2/2-2 Först trodde jag det blev 0 men nu -2 stämmer det?
f(x)= (x-2)^2/(x-2)^3 Om det inte finns på denna, varför inte?
Simon Rybrand (Moderator)
I den första funktionen så saknas en variabel x i formeln, skulle det vara ett x där någonstans?
Det andra uppgiften har ett gränsvärde. Den går mot +∞ om x→2⁺ (från höger) och -∞ om x→2⁻ (från vänster).
Vi kan skriva det så här:
x→2lim(x−2)3(x−2)2=x→2lim(x−2)1
Från höger:
x→2+lim(x−2)1=+∞
Från Vänster:
x→2−lim(x−2)1=−∞
Oscar
Hej, kan du hjälpa mig att förstå det här talet?
Lim går mot -1 x^3-x/1+x
Simon Rybrand (Moderator)
x→−1lim1+xx3−x=
x→−1lim1+xx(x2−1)=(konjugatregeln i nämnaren)
x→−1lim1+xx(x+1)(x−1)=
x→−1limx(x−1)=
x→−1limx2−x=2
Sista steget ges av:
(−1)2−(−1)=1+1=2
Oscar
Hej, jag har en fråga. Kan den här uträkningen stämma?
lim x²+10x+25/x+5=-25-50+25/-5+5=100/-5=-20 ?
x→-5
Simon Rybrand (Moderator)
Hej, nej du jobbar lite fel med gränsvärdet där. En vägledning till detta kan vara följande.
x→5limx+5x2+10x+25
Jobba först med det rationella uttrycket där vi kan faktorisera täljaren med en kvadreringsregel.
x+5x2+10x+25=x+5(x+5)2=x+5
x→5lim(x+5)=10
kotte
Hur kan jag visa att (1+1/n)^n = e då n —> oändligheten?
Simon Rybrand (Moderator)
Hej,
Två sätt att troliggöra (dock ej bevisa) detta är att välja ett antal värden på n för att på så vis se att gränsvärdet går mot e alternativt att rita ut funktionen f(x)=(1+1/x)x och där se att funktionen går mot e.
Det går även att bevisa det hela men det är mycket mer komplicerat.
randsara
Hej jag har en uppgift som jag kunde inte lösa, kan ni hjälpa mig snälla?
beräkna gränsvärdet
lim x–> -4 2x+8/x^2-16
jag fick svar 240, men det känns fel
Simon Rybrand (Moderator)
x→(−4)limx2−162x+8
Du kan förenkla det rationella uttrycket enligt:
x2−162x+8= (x+4)(x−4)2(x+4)= x−42
Gränsvärdet blir då
x→(−4)limx−42=−41
Jill
Hur får du fram värdet – 1/4 ur: 2/x-4?
Simon Rybrand (Moderator)
Så här:
x→(−4)limx−42= −4−42=−82=−41
Etolie
Hej, jag har en uppgift som jag inte kan lösa, kan någon snälla hjälpa mig?
Beräkna gränsvärdena;
Lim x–>3 = 3x^2-18x+27 / x-3
Tänker jag rätt om jag har kommit fram till svaret -6 ?
Simon Rybrand (Moderator)
Hej,
Tror att just svaret -6 inte stämmer.
Här kan du först jobba med det rationella uttrycket först för att förenkla detta:
x−33x2−18x+27=x−33(x2−6x+9)
Nu kan man faktorisera x2−6x+9 så att vi får
x−33(x−3)(x−3)=3(x−3)=3x−9
När x->3 för 3x-9 borde detta alltså blir 0.
Jill
Jag förstår inte svaret du gav Etolie här.
När man har kommit så långt som till 3x-9, tar man inte 9/3 då för att få x ensamt? Eller varför blir det 0? Vet ju att man inte kan sätta in 9/3=3 i ekvationen för då bli nämnaren 0…
Olivia
Hur går det till när man dividerar kvadratrötter?
Min uppgift:
Bestäm ett troligt värde på gränsvärdet genom att beräkna uttryckets värde för mindre och mindre värden på x.
A) lim när x går mot noll, roten ur 1+2x-1 dividerat med 2x
B) lim när x går mot noll, 2^x-1 div med x
Tack!! Bra sida med rättning och förklaringar ^^
Simon Rybrand (Moderator)
A)
Du har alltså
x→0lim2x1+2x−1
Här kan vi skriva om kvoten
2x1+2x−1=2x2x=
2x⋅2x2x=2x1
Nu kan du istället ta reda på
x→0lim2x1=∞
då nämnaren blir mycket liten och därmed går det mot oändligheten. Det kan också vara viktigt att fundera på om vi går från vänster (0⁻) eller höger (0⁺) mot noll. Om vi går från vänster kommer vi ju att behöva ta roten ur ett negativt tal och behöva hantera gränsvärdet med komplexa tal.
Hoppas att detta hjälper dig på vägen!
majanilsson
hur gör man om uppgiften lyder: Beräkna gränsländet lim x->1
(2-roten ur(5x-1))/(1-x^2)
Simon Rybrand (Moderator)
Hej, här får du låta x−>1− (från vänster) och även låta x−>1+ (från höger)
När x−>1− så går uttrycket mot +∞ då nämnaren går mot noll och är positiv.
När x−>1+ så går uttrycket mot -∞ då nämnaren går mot noll och är negativ.
viktorrydberg
Hej!
Jag förstår inte riktigt fråga 3. Jag ska alltså beräkna gränsvärdet lim 1/x när h -> 0. Jag fattar inte riktigt hur jag ska behandla variablerna när de inte är samma variabel. Alltså, Jag hade förstått frågan om den var ”beräkna gränsvärdet lim 1/x när x -> 0”. Står h & x alltid för något speciellt?
Simon Rybrand (Moderator)
Hej, nej du har inte missförstått detta utan det är otydligt i den uppgiften. Vi har tydliggjort detta, säg till om något fortfarande är otydligt.
Emilia
Hej kan någon hjälpa?
Om lim->oändligheten och det står roten ur( 16x/(4x+9)) vad gör man då.?
Simon Rybrand (Moderator)
Jag tolkar det som att du har:
x→∞lim4x+916x
Det du kan göra här är att tänka att när x blir riktigt stort så kommer 9:an inte spelar så stor roll för gränsvärdet. De termer som dominerar för stora x blir
$ \lim\limits_{x \to \infty} \sqrt{\frac{16x}{4x}} =
\lim\limits_{x \to \infty} \sqrt{4} = 2
$
Linnea
Hej!
Jag har en uppgift som jag har problem med att lösa, frågan lyder;
beräkna gränsvärdet av
xn=((n+1)/(n-1))^n
när n går mot oändligheten?
Någon som förstår var jag ska börja någonstans?
MVH
Linnea
Simon Rybrand (Moderator)
Hej Linnea,
Jag tolkar ditt gränsvärde som
n→0lim(n−1n+1)n
Då kan du skriva om kvoten som
(n−1n+1)n=(n−1n+n−11)n
n−1n=1 då n−>∞
och
n−11=0 då n−>∞
Alltså gäller att
n→0lim(n−1n+1)n=1
och xn=x*1 =x
Andrea
Hej,
Kan det saknas gränsvärde?
I min mattebok finns detta
lim x–> 4 x+1/x-4
mitt svar är att gränsvärdet är= +- eternity men i boken står det att gränsvärdet saknas, samm för denna:
lim y—-> -3 4/x+3.
Jag tycker att de e eternity tecknet igen men det står att det saknas gränsvärde.
Vad ser man skillnaden?
Simon Rybrand (Moderator)
Hej,
Om vi tar det första gränsvärdet du har:
x→4limx−4x+1
så är detta inte definierat för att x->4 och vi får inte informationen om att vi går från vänster eller höger. Dvs om x->4⁻ eller x->4⁺ så hade det varit definierat och mycket riktigt blivit -∞ eller +∞ men då vi bara får reda på att det går mot 4 så kommer gränsvärdet hela tiden att variera (oscillera) mellan ±∞ och det går därmed inte att bestämma.
nti_ma3
Hur gör man när man har bråktal som täljare: (1/(3+h) – 1/3)/h
Simon Rybrand (Moderator)
Hej, jag tolkar det som att du har
h→0limh3+h1–31
Här kan vi först jobba med att förenkla detta uttryck genom att skriva täljarens rationella uttryck på samma nämnare. Annars kommer det att bli svårt att beräkna gränsvärdet.
h3+h1–31=
h3(3+h)3−3(3+h)3+h=
h3(3+h)3−3−h=
3(3+h)−h/1h=
3h(3+h)−h=9+h−1
Nu blir det enklare att se att gränsvärdet går
mot 9−1 då h -> 0.
Aggie
Hej!
kan någon förklara lite för mig.
i parentes, hur kom det att
exp 4 f(x+a)=(x+a)^2
exp 5 f(x+h) =(x+h)^2+(x+h)
jag är lite förvirrad/A
Simon Rybrand (Moderator)
Det handlar om vilken funktion du har, dvs i exempel 4 så har du funktionen
f(x)=x2
Då gäller tex att
f(2)=22
f(a)=a2
f(x+h)=(x+h)2
Dvs du byter ut x mot x+h
Hendick
Skitbra sida, men saknar något tal där du dividerar med mer än bara ett tal i nämnare. Typ som detta.
limes x->x
4x^2+3x / x^2+x+10.
Jag bröt ut x i täljaren och fick x(4x+3) / x^2+x+10.
Stryker X i både täljare o nämnare = 4x+3 / x^2+10. Hur gör man sen?
Simon Rybrand (Moderator)
Hej, du har alltså gränsvärdet
x→xlimx2+x+104x2+3x
Tyvärr så kan du inte förenkla det på det viset som du gör då det inte finns ett x vid 10. Ett alternativ hade varit att man kunde ha använt tex en kvadreringsregel för att faktorisera nämnaren på ett bra vis men i detta fall är detta tyvärr svårt. Det har inte blivit ngn siffra eller bokstav fel eller att jag kanske missförstår dig på ngt vis?
Endast Premium-användare kan kommentera.