Författare: Simon Rybrand
Simon Rybrand  Anna Karp
Anna Karp
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Den huvudsakliga användningen av andraderivatan i denna kurs, är att vi med den mycket effektivt kan bestämma extrempunkternas karaktär, samt eventuella inflexionspunkter. Vi kan med andraderivatans hjälp även undersöka hur en graf ser ut och beter sig för olika $x$x -värden.

Andraderivata – derivatans derivata
När man deriverar en derivata, får man något som kallas för andraderivatan. Den betecknas på många olika sätt. Några ser du här.
y′′ f′′(x) dx2d2yd2ydx2
Skrivsättet ′′ uttalas ”bis”.
Andraderivatan motsvarar förändringshastigheten av förändringshastigheten, vilket alltså motsvarar att andraderivatan till en funktion fås genom att man deriverar funktionen två gånger efter varandra.
Ett vanligt exempel för att se sambandet mellan funktionen och första och andraderivatan är att studera en resa med en bil.
Då funktion s(x) beskriver sträckan en bil kört kommer förstaderivatan s′(x) ge hastigheten vid en tidpunkt och andraderivatan s′′(x) i sin tur ge accelerationen vid samma tidpunkt.
Ett annat exempel är att då funktion N(t) beskriver befolkningsmängden ger förstaderivatan N′(t) tillväxthastigheten vid en tidpunkt och andraderivatan N′′(T) förändringen av tillväxthastigheten vid samma tidpunkt.
Så bestämmer du Andraderivata
Exakt samma deriveringsregler används som för förstaderivata. Det vill säga, du deriverar helt enkelt två gånger efter varandra. Vi börjar med ett exempel på andraderivatan av en polynomfunktion.
Exempel 1
Bestäm andraderivatan till f(x)=4x3ƒ (x)=4x3
Lösning
När vi deriverar f(x)ƒ (x) två gånger får vi andraderivatan f′′(x)ƒ ´´(x) .
Vi använder deriveringsregeln för polynomfunktioner
f(x)=kxnƒ (x)=kxn ⇒ f′(x)=n⋅k⋅xn−1ƒ ´(x)=n·k·xn−1
Vi får att
f(x)=4x3ƒ (x)=4x3 ⇒
f′(x)=12x2ƒ ´(x)=12x2 ⇒
f′′(x)=24xƒ ´´(x)=24x
Och nu andraderivatan till en exponentialfunktion.
Exempel 2
Bestäm y′′y´´ till y=2e4xy=2e4x
Lösning
När vi deriverar yy två gånger får vi andraderivatan y′′y´´.
Vi använder deriveringsregeln för exponentialfunktioner
f(x)=Cakxƒ (x)=Cakx ⇒ f’(x)=Cakx⋅k⋅lnaƒ ’(x)=Cakx·k·lna
Vi får att
y=2e4xy=2e4x ⇒
y′=8e4xy´=8e4x ⇒
y′′=32e4xy´´=32e4x
Andraderivatan och extrempunkters karaktär
Som vi tidigare nämnde är den huvudsakliga användningen av andraderivatan i denna kurs, att effektivt bestämma extrempunkternas karaktär, eventuella inflexionspunkter och undersöka hur grafen beter sig för olika xx -värden.
Det är nämligen så att om andraderivata är negativ för xx -värdet som motsvarar förstaderivatans nollställe, så säger man att kurvan är konkav för alla xx i intervallet runt maximipunkten.

Förstaderivatans är avtagande runt maximipunkten, den går från positiv till negativ via värdet noll. Det ger att andraderivatan är negativ i maximipunkten.
Positiv andraderivata
Om funktionen fƒ och f′ƒ ´ är deriverabar på intervallet a<a< x<x< bb gäller att
fƒ är konkav i intervallet om och endast om f′′(x)≤0ƒ ´´(x)≤0 för alla xx i intervallet.
Om andraderivata däremot är positiv för xx -värdet som motsvarar förstaderivatans nollställe, så säger man att kurvan är konvex för alla xx i intervallet runt minimipunkten.

Förstaderivatans är växande runt minimipunkten, den går från negativ till positiv via värdet noll. Det ger att andraderivatan är positiv i minimipunkten.
Positiv andraderivata
Om funktionen fƒ och f′ƒ ´ är deriverabar på intervallet a<a< x<x< bb gäller att
fƒ är konvex i intervallet om och endast om f′′(x)≥0ƒ ´´(x)≥0 för alla xx i intervallet.
Med andra ord kan på detta sätt undersöka karaktären på förstaderivatans nollställen med hjälp av andraderivatan och snabbt bestämma om extremvärdet motsvarar en maximi- eller minimipunkt.
Exempel 3
Bestäm minimipunkten till funktionen f(x)=2x3−6x2ƒ (x)=2x3−6x2.
Lösning
Minimipunkten återfinns där derivatan är lika med noll. Vi börjar med att ta fram derivatan
f(x)=2x3−6x2ƒ (x)=2x3−6x2 ⇒ f′(x)=6x2−12xƒ ´(x)=6x2−12x
och sätter derivatan lika med noll för att bestämma extrempunkternas xx -värden
6x2−12x=06x2−12x=0 Bryt ut 6x6x i VL
6x(x−2)=06x(x−2)=0
Med nollproduktmetoden får vi att
6x=06x=0 ger x1=0x1=0
x−2=0x−2=0 ger x2=2x2=2
Nu vet vi vid vilka xx-värden tangenters lutningen på grafen till f(x)ƒ (x) är lika med noll. Men andra ord, extrempunkterna. För att bestämma extrempunkternas karaktär, det vill säga om det är maximi- eller minimi, eller om punkten rent utav är en terasspunkt, använder vi andraderivata..
När vi deriverar f(x)ƒ (x) två gånger får vi andraderivatan f′′(x)ƒ ´´(x).
f′(x)=6x2−12xƒ ´(x)=6x2−12x ger att f′′(x)=12x−12ƒ ´´(x)=12x−12
Vi sätter extrempunkternas xx-värden i andraderivatans funktion för att ange om den är negativ, positiv eller lika med noll.
f′′(0)=12⋅0−12=−12ƒ ´´(0)=12·0−12=−12 En negativ andraderivata innebär en maximipunkt
f′′(2)=12⋅2−12=12ƒ ´´(2)=12·2−12=12 En positiv andraderivata innebär en minimipunkt
Vi ser utifrån ovanstående beräkning att x=2x=2 ger minimipunkten.
Vill vi ange punkten på grafen som motsvarar extrempunkten beräknar vi extremvärdet för extrempunkten. Det gör vi genom att sätta in x=2x=2 i vår ursprungliga funktion.
f(2)=2⋅23−6⋅22=16−24=−8ƒ (2)=2·23−6·22=16−24=−8
Vi har alltså en minimipunkt på grafen till funktionen f(x)ƒ (x) i punkten(2,−8)(2,−8). Men minimipunkten anger endast med xx-värdet.
Om andraderivatan lika med noll
Om både första- och andraderivatan är lika med noll måste vi undersöka derivatans karaktär närmre med teckenstudier.
Inflexionspunkt
Den punkt x=ax=a där funktionen byter från att vara konvex till konkav eller tvärtom kallas för en inflexionspunkt.
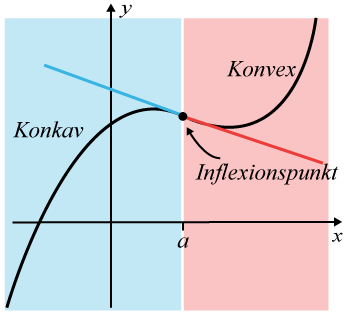
I denna kursen kommer vi titta lite extra på den inflexionspunkt som kallas för terrasspunkt. Inflexionspunkten i figuren ovan är ingen terrasspunkt.
En terrasspunkt är en punkt som är både en inflexionspunkt och en stationär punkt. Alltså en punkt med egenskapen att både första och andraderivatan är lika med noll i punkten.
Det leder till att för inflexionspunkter x=ax=a, och därmed även i terrasspunkter, har förstaderivatan en extrempunkt.

Om funktionen är växande eller avtagande kring terasspunkten, det vill säga punkter där både f′(x)ƒ ’(x) och f′′(x)ƒ ´´(x) är lika med noll, bestämmer du alltså på ett annat sätt, tex med hjälp av en teckentabell. Hur vi gör det tittar vi på i lektionen nollställen och teckentabeller.
Exempel i videon
- Bestäm f′′(x)ƒ ´´(x) då f(x)=3x3+x2−3xƒ (x)=3x3+x2−3x
- Använd andraderivata för att skissa grafen till funktionen f(x)=4x3−6x2+1ƒ (x)=4x3−6x2+1
- Skissa grafen till funktionen f(x)=2x3−2ƒ (x)=2x3−2
Kommentarer
e-uppgifter (6)
1.
(1/0/0)E C A B P 1 PL M R K Bestäm andraderivatan till f(x)=x4ƒ (x)=x4
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B P 1 PL M R K Bestäm andraderivatan till f(x)=2x3ƒ (x)=2x3
Svar:Ditt svar:Rätt svar: f′′(x)=12x(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: AndraderivataRättar...3.
(1/0/0)E C A B 1 P PL M R K Bestäm f′′(x)ƒ ´´(x) då f(x)=e2x−10xƒ (x)=e2x−10x
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K För andraderivatan gäller att f′′(x)>0ƒ ´´(x)>0 i området kring x=ax=a .
Välj vilket av nedanstående alternativ gäller för f(x)ƒ (x) i x=ax=a.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm f′′(x)ƒ ´´(x) då f(x)=3x4+x3−2xƒ (x)=3x4+x3−2x
Svar:Ditt svar:Rätt svar: f′′(x)=36x2+6x(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B 1 P PL M R K I vilken punkt är f′(x)=0ƒ ´(x)=0 och f′′(x)<0ƒ ´´(x)<0 ?
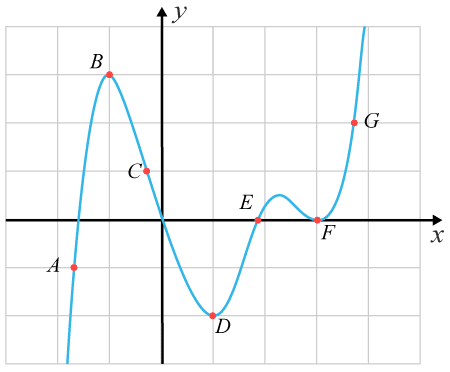 Svar:Ditt svar:Rätt svar: I Punkt B(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: I Punkt B(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (2)
7. Premium
(1/1/0)E C A B 1 P PL M R 1 K Vilken av graferna nedan skulle kunna vara andraderivatan till funktionen f(x)=x4+10x3−36x2ƒ (x)=x4+10x3−36x2 ?
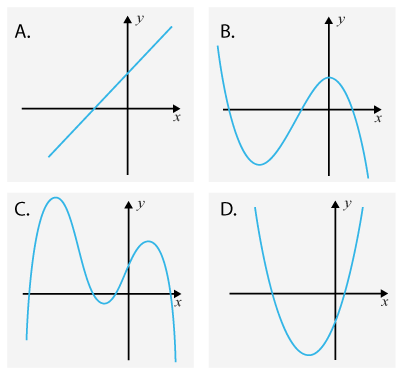
Ange ditt svar med bokstaven för grafen, men träna på att motivera ditt val.
Svar:Ditt svar:Rätt svar: Graf D då andraderivatans graf i denna uppgift är en andragradsfunktion då det är två gradtal lägre än den ursprunliga fjärdegradaren.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: AndraderivataRättar...8. Premium
(0/2/0)E C A B 1 P PL M R 1 K Vilket påstående är INTE sant?
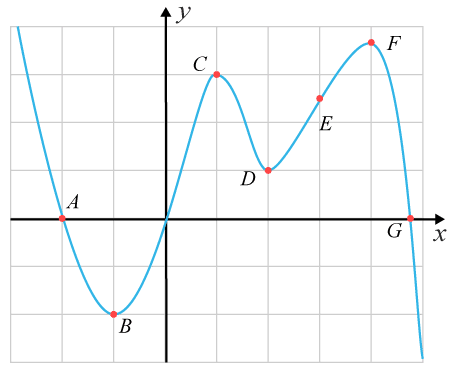 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (2)
9. Premium
(0/1/2)E C A B P 1 PL M R 1 1 K Neo påstår att f′′(x)>0ƒ ´´(x)>0 för alla xx om
f(x)=ax4+bx2ƒ (x)=ax4+bx2
och aa och bb är två positiva konstanter som tillhör de reella talen.
Håller du med Neo?
Ange svaret Ja eller Nej, men öva på att bevisa ditt påstående.
Svar:Ditt svar:Rätt svar: Ja, Neos påstående stämmer.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(0/0/3)E C A B P 1 PL 1 M R 1 K En inflexionspunkt är en punkt där funktionen går från att ha varit konvex till att vara konkav eller tvärtom.
Punkten (a, b)(a, b) är en inflexionspunkt på grafen till funktionen f(x)=x3+6x2ƒ (x)=x3+6x2.
Bestäm aa och bb och ange inflexionspunkten i koordinatform.
Svar:Ditt svar:Rätt svar: (−2,16)(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Linnea Johansson
Hej!
Man kan tolka texten väldigt fel i uppgift 3. När f(x)=0 kan man tro att derivatansfunktion är 0 vilket medför att det är en linjär funktion från början. Det framgår inte att det är i punkten X som derivatan är 0.
Anna Admin (Moderator)
Hej Linnea.
Jag har nu försökt formulera om frågan och hoppas att du tycker den blev tydligare. Lycka till med derivatan!
Clockwork Cadaver
Bilden laddar inte i uppgift 7, varken i Firefox eller Internet explorer utan tillägg.
Simon Rybrand (Moderator)
Tack för kommentar, det är fixat!
Rasmus Mononen
Skumma svar i uppgift 5 och 7.
// Rasmus
Sebastian Sollerman
I uppgift 7 står det i facit följande: f´´(C)=f´(F)
stämmer inte då andraderivatan för C positiv och första derivatan för F negativ
Vad jag kan se i grafen så är F”(C) en maximipunkt och måste väl där med ha negativ andra derivata?
I uppgift 8 står funktionen f(x) = x^3 + 2x^2
Men svaret i facit är beräknat utifrån f(x) = x^3 + 6x^2…..
Simon Rybrand (Moderator)
Hej
Vi kikar på detta.
Jonatan Wennberg
Ange koordinaterna för extrempunkterna till funktionen
f(x) = x5 – 5x
Hej skulle behöva hjälp med denna då jag sitter fast..
Simon Rybrand (Moderator)
Se svar här:
/lektioner/nollstallen-och-teckentabell/
Julia Ojeda Ottosson
Hej, i min fråga står det: För funktionen f gäller att f(x)=2/x^2 + 2x
Men jag förstår inte hur man gör i division. Och vad innebär f’=0 ? Jag har enbart sett beskrivningar i min mattebok och här på hemsidan om y´=0 men ingen f´=0.
Mvh Julia
Mikael144600
Hej!
Jag har en fråga gällande uppgift 4: Beräkna y″ för y=−2sin(2x).
Mellan första derivatan och andra derivatan har basen 4 bytt tecken (från negativ till positiv), varför då?
Simon Rybrand (Moderator)
Hej
Det beror på att derivatan för cos(x) är -sin(x). Du deriverar ju först så att du får cos som den yttre derivatan. Nästa gång vi deriverar för att få andraderivatan så deriverar du cos till sin.
Hélèna Osseyran
Hej!
Jag har en fråga gällande uppgift 4: Beräkna y″ för y=−2sin(2x)
Vilken regel använder ni er av då? Och hur vet man när man inte skall derivera med produktregel eller kedjeregel? Jag fick att y prim blev -4cos. Vad gör jag fel då?
Tack på förhand!
/Förvirrad derivata
Simon Rybrand (Moderator)
Hej, i den funktionen så behöver vi tänka på att vi har en inre funktion 2x (i parentesen) så då används kedjeregeln för att derivera detta.
Jag gjorde så att jag uppdaterade förklaringen och gjorde den mer utförlig så kika gärna på den igen så hoppas jag att det blir tydligare!
Pedro Veenekamp
Har inte än vaknat … en försök till:
”Om jag inte har det fel så är f´´(x) = 0 om f´(x) = a”
Pedro Veenekamp
Ny ser jag att jag skrev nåt fel … det skulle stå:
”Om jag inte har det fel så är f´´(x)= = om f´(x) = a ”
där a är ett realtal.
Pedro Veenekamp
Hej!
Kan du förklara hur f´´(x) > 0 om f´(x) = 0 (frågan 3)
Om jag inte har det fel så är f´´(x) = 0 om f´(x) = 0
f´(x) är lika med noll när f(x) är en rätt linje, eller hur?
Tack för hjälpen!
Falah
Hej! Om man har f”(x)=0 ?
Vad betyder det?
Simon Rybrand (Moderator)
Det skulle kunna betyda (troligtvis är det så) att du har hittat en terrasspunkt.
qwert
Hej!
Jag har problem med denna uppgiften, jag kan stegen men lyckas inte få det till cirka 259.
Beräkna f”(1) om
f(x)=5^2x + x
Simon Rybrand (Moderator)
Funktionen blir enklare att derivera om du skriver om den på följande vis:
f(x)=52x+x=25x+x
Då får du
f′(x)=ln25⋅25x+1
f′′(x)=(ln25)2⋅25x
och
f′′(1)=(ln25)2⋅251=259
nti_ma4
Hej!
Jag har alltid lärt mig att när en funktion går uppåt runt en punkt(en minimipunkt) så heter det att den är konvex, inte konkav uppåt. Sen när den går neråt runt en punkt(maximipunkt) så heter det att grafen är konkav. Har jag lärt mig fel?
nti_ma4
// Jerry Skarp
Simon Rybrand (Moderator)
Hej,
Egentligen så är det lite lurigt att använda konkav (buktar inåt) och konvex (buktar utåt) när funktioner beskrivs då man ofta använder begreppen när linser beskrivs. I en konkav lins buktar bägge sidor inåt vilket är svårt att likna vid en funktion på samma vis. Jag brukar använda begreppet konkav uppåt när vi har en minimipunkt och konkav nedåt när vi har en maximipunkt.
Säg till om detta fortfarande är oklart på något vis!
Jeremy Barnes
Konkav = har min punkt
Konvex = har max punkt
Annat verkar tokigt, och att blanda in linser i leken gör knappast saken tydligare.
Jakob Carlsson
Hej!
Jag har ett tal som ser ut så här 2x^1/2 + x^-1/2 bestäm f'(4).
jag förstår inte genom videon hur jag ska göra, kan du förklara?
Simon Rybrand (Moderator)
Hejsan Jakob, det här är en så kallad potensfunktion och det kan vara bra att kika på genomgångarna om derivata för potensfunktioner så kommer du säkert att förstå mer kring detta. I just detta fall gäller att:
f(x)=2x1/2+x−1/2
f′(x)=x−1/2–21x−3/2=x1/21–2x3/21
Endast Premium-användare kan kommentera.