Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 3b
/ Derivatan och grafen
Derivatans nollställen och teckentabell
Innehåll
Bestäm extrempunktens karaktär
I den här lektionen tittar vi på en metod/strategi för hur du metodiskt kan undersöka hur en funktion växer och avtar i olika intervall och punkter.
Där funktionens derivata har ett nollställe har funktionen en stationär punkt. Det vill säga en maximipunkt, minimipunkt eller en terrasspunkt. Vi avgör karaktären på den stationära punkten, det vill säga vilken av dessa tre den är, på följande vis.
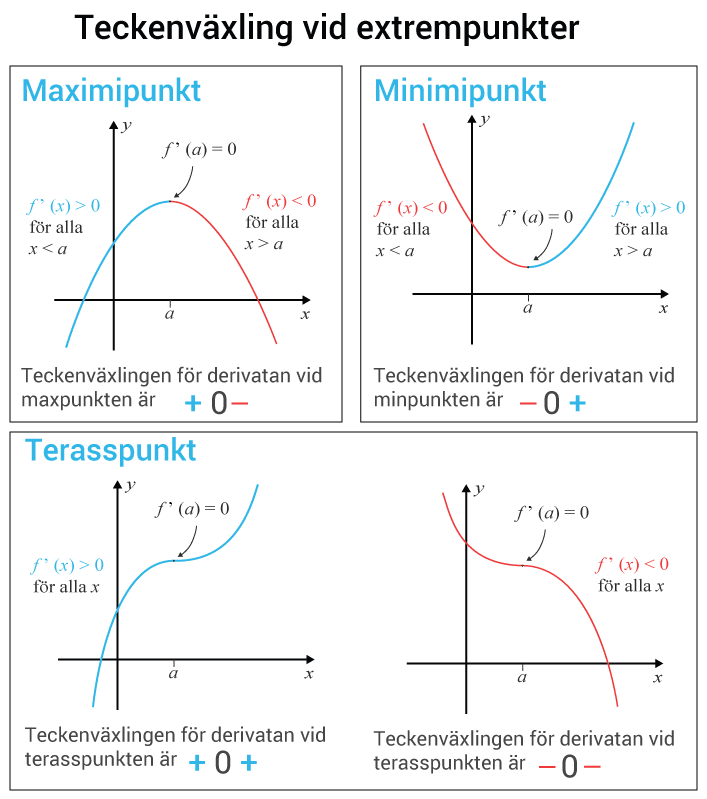
- Om det är en maximipunkt så växer funktionen innan punkten och avtar efter punkten. Vi har teckenväxlingen $+0-$+0−
- Om det är en minimipunkt så avtar funktionen innan och växer efter punkten. Vi har teckenväxlingen $-0+$−0+
- Om det är en terrasspunkt så växer funktionen innan och efter alternativt avtar innan och efter punkten. Vi har teckenväxlingen $+0+$+0+ eller $-0-$−0−
Strategi
Den strategi som presenteras i videon är följande.
- Derivera funktionen $f\left(x\right)$ƒ (x).
- Lös ekvationen $f'(x) = 0$ för att bestämma de $x$x-värden som motsvarar derivatans nollställen. Dessa nollställen motsvarar funktionens extrempunkter.
- Bestäm $f(x)$ för derivatans nollställen.
- Undersök derivatan mellan nollställena för att se om funktionen är avtagande eller växande i intervallet mellan nollställena. Det räcker att du beräknar derivatans värde för ett $x$x-värde i intervallet, då det inte kan ske en så kallad teckenväxling mellan derivatans nollställen. Om derivatan är positiv är funktionen växande i punkten, är den negativ är den avtagande.
- Skissa kurvan. Det sista steget är att skissa grafen till funktionen. Vi har nu fyllt i allt vi undersökt i vårt teckenschema, så detta sista steg brukar vara ganska enkelt. Men det är ändå viktigt för att förstå hur funktionen ser ut.
Skissa funktioner med hjälp av en teckentabell
Genom att föra in dina resultat i en teckentabell får du en tydlig bild över grafens utseende. Det leder till att det blir enklare att göra en korrekt skiss av kurvan och dra korrekta slutsatser.
Exempel 1
Skissa kurvan $f\left(x\right)=x^3-1,5x^2-6x$ƒ (x)=x3−1,5x2−6x med hjälp av en teckentabell.
Lösning
En teckentabell kan se lite olika ut, men ett sätt är så här. Vi skriver till höger en kolumn med några värden vi vill undersöka.
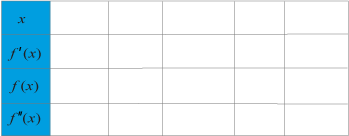
Börja med att beräkna derivatans nollställen. $f\left(x\right)=x^3-1,5x^2-6x$ƒ (x)=x3−1,5x2−6x har derivatan $f'(x)=3x^2-3x-6$ƒ ’(x)=3x2−3x−6. Vi sätter derivatan lika med noll för att bestämma extrempunkterna.
$3x^2-3x-6=0$3x2−3x−6=0
$x^2-x-2=0$x2−x−2=0
$x_{1,2}=$x1,2=$\frac{1}{2}\pm\sqrt{\left(\frac{1}{2}\right)^2-\left(-2\right)}$12 ±√(12 )2−(−2)
$x_{1,2}=$x1,2= $\frac{1}{2}\pm\sqrt{\frac{9}{4}}$12 ±√94
$x_{1,2}=$x1,2= $\frac{1}{2}\pm\frac{3}{2}$12 ±32
$x_1=-1$x1=−1 och $x_2=2$x2=2
Vi fyller i derivatans nollställen i tabellen enligt nedan. Vi vet nämligen att $f'(x)=0$ƒ ’(x)=0 då $x=-1$x=−1 och $x=2$x=2.
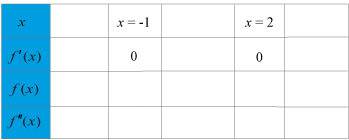
Därefter väljer vi ett värde på $x$x som är mindre, ett mellan och ett större än nollställena och beräknar derivatan för dessa. Det gör vi för att avgöra om funktionen är växande eller avtagande före, mellan och efter nollställena. Vi kan välja precis vilket $x$x -värde som helst, men har här valt $x=-2$x=−2 vilket är ett värde mindre än det minsta nollstället $x=-1$x=−1.
$f'(-2)=3\cdot\left(-2\right)^2-3\cdot\left(-2\right)-6=12>0$ƒ ’(−2)=3·(−2)2−3·(−2)−6=12>0 vilket anges med ett $+$+ i tabellen. Derivatan är alltså positiv i intervallet $x<-1$x<−1.
Därefter beräknar vi derivatan för $x=0$x=0 för att ge derivatan i intervallet mellan nollställena.
$f'(0)=3\cdot0^2-3\cdot0-6=-6<0$ƒ ’(0)=3·02−3·0−6=−6<0 vilket anges med ett $-$− i tabellen. Derivatan är alltså negativ i intervallet $-1$−1 $x<2$x<2 .
Till sist väljer vi $x=3$x=3.
$f'(3)=3\cdot3^2-3\cdot3-6=12>0$ƒ ’(3)=3·32−3·3−6=12>0 vilket anges med ett $+$+ i tabellen. Derivatan är alltså positiv i intervallet $x>2$x>2 .
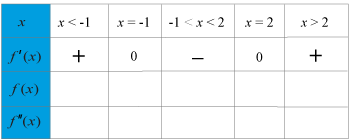
Genom att rita pilar i positiv och negativ riktning på raden för $f\left(x\right)$ƒ (x) ges en ”bild” av hur funktionen $f\left(x\right)$ƒ (x).
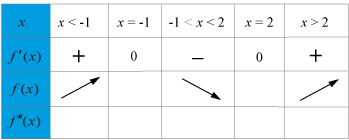
Är derivatan positiv är funktionen växande vilket motsvarar en pil uppåt, positiv riktning.
Är derivatan negativ är funktionen avtagande vilket motsvarar en pil nedåt, negativ riktning.
Teckenväxlingen $+0-$+0− ger en maximipunkt.
Teckenväxlingen $-0+$−0+ ger en minimipunkt.
Vi kan också använda andraderivatan för att bestämma extrempunktens karaktär.
$f”(x)=6x-3$ƒ ”(x)=6x−3 ger att
$f”(-1)=6\cdot\left(-1\right)-3=-9<0$ƒ ”(−1)=6·(−1)−3=−9<0 vilket ger en maximipunkt.
$f”(2)=6\cdot2-3=9>0$ƒ ”(2)=6·2−3=9>0 vilket ger en minimipunkt.
Genom att beräkna $f\left(-1\right)$ƒ (−1) och $f\left(2\right)$ƒ (2) får vi även $y$y-koordinaten tillhörande extrempunkterna.
Vi vet att $f\left(x\right)$ƒ (x) är en positiv tredjegradsfunktion. Vi markerar maximi- och minimipunkterna och sammanbinder till en skiss.
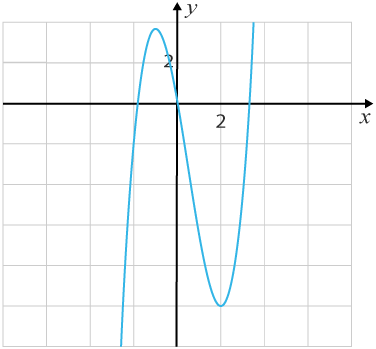
Med lite övning kommer du förhoppningsvis kunna skissa i stort sett vilken funktion som helst.
Exempel i videon
- Använd teckentabell för att skissa grafen till funktionen $f\left(x\right)=2x^2-4x$ƒ (x)=2x2−4x
- Använd teckentabell för att skissa grafen till funktionen $f\left(x\right)=2x^3-3x^2$ƒ (x)=2x3−3x2
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (7)
-
1. Premium
Lös ekvationen $f'(x)=0$ƒ ’(x)=0 med hjälp av grafen i figuren nedan.
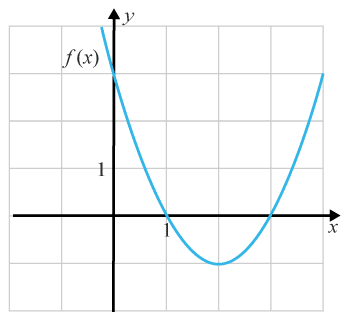Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar...2. Premium
Studera teckentabellen nedan och ange för vilket $x$x -värde funktionen $f(x)$ƒ (x) har en lokal maximipunkt.
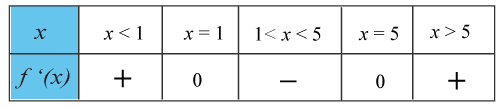Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Derivatans nollställen och teckentabellLiknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar...3. Premium
Studera teckentabellen nedan och ange för vilket x-värde funktionen $f(x)$ har en lokal maximipunkt.
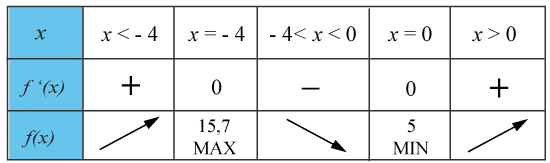Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar...Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut!4. Premium
För vilka $x$x gäller att $f'(x)\le0$ƒ ’(x)≤0?
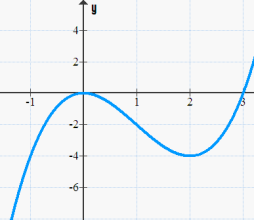Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen nollställen och teckenschemaRättar...5. Premium
Studera teckentabellen nedan och ange i vilket intervall funktionen $f(x)$ƒ (x) är avtagande.
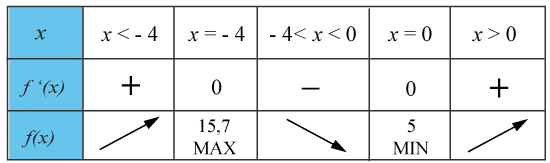Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: derivatan skissa grafer teckentabellRättar...6. Premium
Studera teckentabellen nedan och ange i vilket intervall funktionen $f(x)$ƒ (x) är växande.
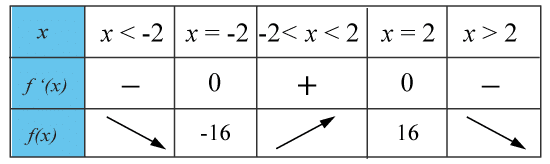Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar...7. Premium
För funktionen f gäller att $f(x)=x^3-3x^2$ƒ (x)=x3−3x2. Bestäm med hjälp av derivata koordinaterna för eventuella maximi-, minimi- och terrasspunkter för funktionens graf.
Bestäm också karaktär för respektive punkt, det vill säga om det är en maximi-, minimi- eller terrasspunkt.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...c-uppgifter (3)
-
8. Premium
Ange med hjälp av en teckentabellen koordinaterna till den punkt på grafen till funktionen $f(x)=x^3+3x^2$ƒ (x)=x3+3x2 där eventuella minimipunkter återfinns.
Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar...9. Premium
Studera teckentabellen nedan och välj, genom att göra egna teckentabeller till alternativen, vilken av funktionerna som tabellen tillhör.
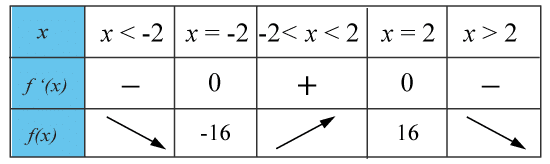Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar...10. Premium
För en polynomfunktion $f$ƒ gäller att derivatan har endast två nollställen. Tabellen visar derivatans tecken för några olika värden på $x$x.
Använd koordinatsystemet nedan och skissa en möjlig graf till funktionen $f$ƒ .
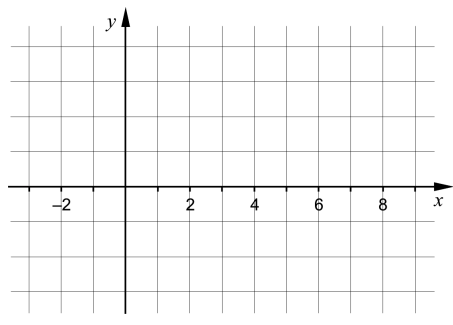Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Derivatans nollställen och teckentabellLiknande uppgifter: skissa grafer teckentabellRättar...a-uppgifter (1)
-
11. Premium
Om $f'(a)=0$ƒ ’(a)=0 och $f’\left(x\right)$ƒ ’(x) har teckenväxlingen $+0+$+0+ eller $-0-$−0− vid $x=a$x=a, så är $\left(a,f\left(a\right)\right)$(a,ƒ (a)) en terrasspunkt.
Låt $f\left(x\right)=x^3+kx^2+3x$ƒ (x)=x3+kx2+3x där $k$k är en konstant.
För vilket värde på $k$k har funktionen en terrasspunkt?
Svar:Ledtråd
Ledtråd 2
Ditt svar:Rätt svar:💡 Enheten saknas i ditt svar💡 Tänk på att förkorta bråket till enklaste form💡 Räkna ut så långt du kan och slå ihop det som går💡 Bryt ut så mycket som möjligt — finns det något gemensamt kvar i parentesen?Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Derivata Derivata och kurvor derivatan och grafen Matematik 3 nollställen och teckenschemaRättar... -
-
Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut! -
Uppgiften är en del av en abc-fråga. Vad vill du göra?
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
John B
Hej, jag förstår inte varför koordinaterna blir (0,0) i fråga 7. Mvh
Daniel Jönsson
”Med lite övning så kommer du förhoppningsvis kunna skissa i stort sätt vilken funktion som helst”
Ni menar att man kan skissa den grovt för att få en överblick över hur den ter sig?
Alexander Y
istället för att skriva
f´(x)=4x-4
f'(x)=0
4x-4=0
…
kan man skriva
f´(x)=4x-4
4x-4=0
4x=4
…
för anledningen är den att jag skrivit så i början och vet inte om det kommer till att bli någon konstighet sen på provet. Håller mig gärna till det allmänna sättet 🙂
Lisa Rahmani
Borde inte funktionen vid 04:13 ha två nollställen eftersom det är en andragradsfunktion? Vet att funktionerna inte måste ha detta utan kan ha UPP till två men hur vet man det? Varför svarade du inte t.ex. x = +-1 istället för bara 1?
Lisa Rahmani
Ok, så man kollar på derivatans funktion när man gör tabellen, inte funktionens. Tack!
Jonatan Wennberg
Ange koordinaterna för extrempunkterna till funktionen
f(x) = x^5 – 5x
Behöver hjälp med denna då jag hade prov idag och blev osäker på om jag svarade rätt..
Mattefreak
Jag försöker bestämma algebraisk lokala/globala extrempunkter till funktionen
f(x)=6x-x^3 på intervallet (-2 < x < 4)
Deriverar funktionen och får ut
6x-3x^2
x1= roten ur 2 & x2= negativ roten ur 2 är dessa lokala extrempunkter?
Får även fram att globala extrempunkterna bör vara 4;-40 och 1,5 stämmer detta? Vad är de lokala globala hur ska jag ställa upp detta korrekt?
Mattefreak
skrev bara fel 6-3x^2 ska det vara, får ändå inte ihop det
Elna Cornelia Karlsson
I filmen står det (4:36) att det är ett nollställe när x=1. Detta måste ju vara fel, y ska ju vid ett nolställe vara lika med noll och i detta fallet är jui y= -2. Det är väl snarare en extrempunkt i x=1 eller är det jag som är ute och cyklar?
Lovisa Ekegren Scheffer
Hej! Tack för bra genomgångar, känner att jag förstår mycket mer än innan! Men har väldigt svårt för funktioner som har mer än en extrem/terasspunkt. Jag förstår att det är då derivatan = 0 som det är en sån punkt, men tycker det är svårt att räkna ut i uppgifterna. Ex:
f(x) = x^3 + 6x^2 – 10
f(x) = 2x^3 + 3x^2 – 12x
nti_ma3
Hej, i sista exemplet i videon så räknar du ut derivatan mellan de två max-min-punkterna. Var inte det onödigt, man kan väl anta att funktionen måste avta eftersom f(x) går från 0 till -1?
nti_ma3
Hej! Jag undrar över tal 4018c i exponent3b, hur deriverar man 1-4x^2-2x^3-x^4/4 , jag måste deriverat fel för jag fick helt fel svar till slut. Tack på förhand
Ida
Hej!
I matematik C boken av Holström, uppgift 2120 så frågar dom efter i vilka punkter g'(x) är noll baserat på en bild på grafen g'(x).
Detta antar jag är när grafen visar k=0. Men de menar på att det är när kurvan skär i x-axeln. Jag trodde att det var fallet ifall dom skulle ha frågat efter g(x)=0, alltså inte derivatans nollställe utan funktionens. Vad är det jag inte förstått?
Vore väldigt tacksam ifall du hittar tid till detta. Tack på förhand!
Ida
Bra förklarat, nu förstår jag. Tack så mycket!
mikaelhagfeldt@gmail.com
Jag blev lite förvirrad av genomgången. Är inte nollställen där funktionen skär x-axeln, dvs där y=0? Hur kan en extrempunkt vara samma sak som ett nollställe? Eller är det skillnad på ett nollställe för en vanlig funktion och ett nollställe för en derivata? Jag vet att om f'(x)=0 så har funktionen nått en extrempunkt av något slag, men har vi f(x)=0 så har vi stött på funktionens rötter? Kan rötterna till en funktion vara samma sak som funktionens extrempunkter? Förstår knappt vad jag själv skriver men det slår runt i huvudet på mig.
Tack på förhand!
Grillska gymnasiet Uppsala
Hej. Jo, du måste ändra teckentabellen så att det står maxpunkt och minpunkt där derivatans värde är noll. Det blir helt fel att kalla det för nollställen. Annars gör ni föredömliga genomgångar tycker jag.
/Anders.
Denise 123
Hej jag undrar hur man bestämmer koordinaterna för -3x^5+5x^3?
Har problem efter att jag har deriverat Y’=-15x^4 + 15x^2
Hur gör man om det är upphöjt till 4 ??
carlitav
jag måste också säga att jag tycket videon vart helt genial! Super pedagogisk! Tack ska ni ha!!!
carlitav
åhhhhhh.. haha det klart! 🙂 ! tack!!!
carlitav
Hej!
Jag känner mig förvirrad på uppgift 3. Eftersom ekvationen har två x värden:
x₁=0 vilket ger y=f(0)=0
och
x₂=−2 vilket ger y=f(−2)=−8+12=4,
bör det inte finnas två minimi-eller maximipunkter?
Jag trodde nämligen att svaret var (0,0) (-2,4)
Jag förstår inte varför den bara en har minimipunkt som skär i (0.0).
Tack på förhand!
fatima94
Hej! kan du hjälpa med mig att lösa den här uppgiften:
bestäm funktionens extrempunkter mha teckenstudier.
funktionen är f(x)=x^3-12x
yaijamal
hej!kan du hjälpa mig lösa funktionenf(x)=3x^2-4x^2 med derivatans definition.tack på förhand!
Lina
och denna
Vilken värdemängd har funktionen f(x) = 3 + x^2 ?
Tack på förhand!! 😀
Lina
Tacktacktack!!! 😀
Lina
Hej! Kan jag få hjälp med denna?? 🙂
Du har funktionen y = x^2 + 14x +20
Ange symmetrilinjen
DelToro
Bestäm konstanten A i funktionen y = x2 -2Ax + A så att funktionen får endast ett nollställe. hur räknar jag ut denna?
Scaleform2012
Hej har matte prov på måndag och har fastnat med ett tal: Undersök om punkten (0,0) är en maximi, minimi eller terrass punkt.
a) $ y = 2x^4 -x^2 $
b) $ y= 3x^2 $
Alltså ska jag derivera funktionen sen hitta noll ställerna och sedan göra ett teckenschema?
Kan visa hur jag ska räkna ut talet 🙂
Scaleform2012
Tack ! 🙂
Scaleform2012
Sitter fast med ett tal.. Bestäm eventuella maxi,minimi och terrasspunkter till funktionerna. Funktionerna ska ej ritas.
a) $ y = 4x – x^2 $
b) $ y = x^2/2 + 3 $
Scaleform2012
Tack så mycket ! 😀
Endast Premium-användare kan kommentera.