Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Vad är linjär optimering?
Linjär optimering är en metod för att hitta ett så bra, eller optimalt, värde som möjligt utifrån en viss situation. En situation med ett antal olika villkor. Villkoren definieras utifrån situationens förutsättningar. Det kan handla om många olika begränsningar med ofta är de ekonomiska, rumsliga, mängd eller tidsmässiga begränsningar.
Begränsningarna kallas för villkor och beskrivs i denna kurs som linjära olikheter. Dessa olika villkor kommer tillsammans att begränsa ett område i planet. Alla punkter i området kommer att klara alla begränsningar, uppfylla alla villkor, och därmed vara värden som är möjliga utifrån villkoren. Men linjär optimering möjliggör vi att inte bara hitta alla möjliga, utan även det bästa värdet.
För att kunna räkna med linjär optimering behöver vi först repetera och introducera några begrepp. Nämligen olikheter, plan, halvplan, räta linjens ekvation och linjära ekvationssystem.
Olikheter
En olikhet beskriver ett storleksförhållande för t.ex. en variabel. Vanligtvis används symbolerna <, >, ≥, ≤ för att beskriva olikheten. Några exempel kan vara
- x <999 utläser vi som x är mindre än 999.
- x≥−55 utläser vi som x är större eller lika med −55
- 0≤x≤10 utläser vi som x är större eller lika med 0 och mindre eller lika med 10.
På detta sätt kan man på ett effektivt sätt beskriva ett oändligt antal olika värde på en variabel i ett intervall.
På liknade sätt kan vi med linjära olikheter beskriva ett oändligt antal önskvärda punkter i ett plan.
Plan och Halvplan
Med ett plan menas ett tvådimensionellt geometriskt objekt som alltså har en höjd och en bredd men inget djup. I genomgången beskriver vi planet med hjälp av ett koordinatsystem så att det blir tydlig vad som är x-, respektive y-led.
Ett halvplan skapas då planet avgränsas i två delar av exempelvis en rät linje.
Olikheterna avgör om man avser planet ovan eller under linjen.
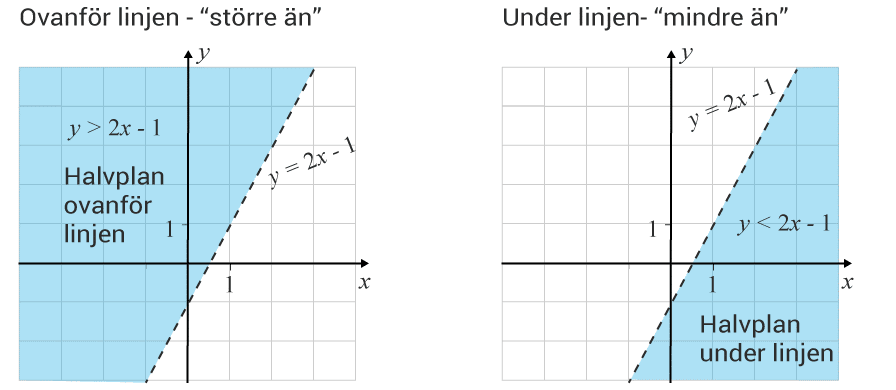
Ett trick för att kunna avgöra om planet är över eller under linjen kan vara att du för din hand mot linjen ovan ifrån med handflatan neråt. När någon del av handen rör linjen landar den på den och resten av handen måste vinklas för att även den land på linjen. Det område som är under handen är under linjen. Det område som är ovanför handen är även ovanför linjen.
När tillhör punkterna på linjen halvplanet?
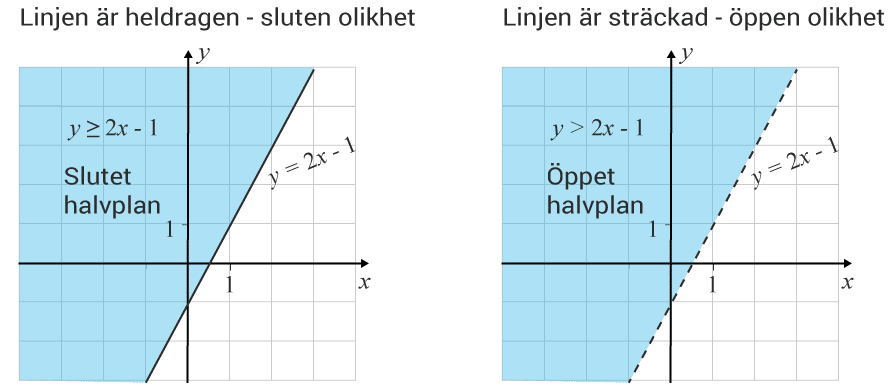
≤,≥≤,≥ olikheterna är slutna. Då tillhör alla punkter på linjen halvplanet. Linjen som delar planet är heldragen.
<,><,> olikheterna är öppna. Då tillhör ingen av punkterna på linjen halvplanet. Linjen som delar planet är streckad.
Exempel i videon
- Företaget ekonomibröderna AB erbjuder två kurser i bokföring. De kan max ha 80 kurser per år med totalt max 1000 deltagare. Intäkterna ges av tabellen i genomgången. Grundkursen i bokföring ger intäkter på 4000 kr och att de max kan ha 10 deltagare per kurs. Fortsättningskursen ger intäkter på 6000 kr och att där kan de max ha 20 deltagare per kurs. Frågan är nu hur många av varje typ av kurs företaget ska hålla för att maximera sina intäkter under ett år?
- Beskriv x≥1 på en tallinje.
- Beskriv x>1 på en tallinje.
- Beskriv −1< x≤4 på en tallinje.
- Markera y≥x+1 i planet.
Kommentarer
e-uppgifter (4)
1.
(1/0/0)E C A B 1 P PL M R K Vilken olikhet beskriver området som är markerat på tallinjen?
 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B 1 P PL M R K Vilken olikhet beskriver området som är markerat på tallinjen?
 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
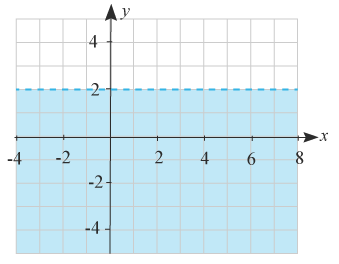 Svar:Ditt svar:Rätt svar: y<2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: y<2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
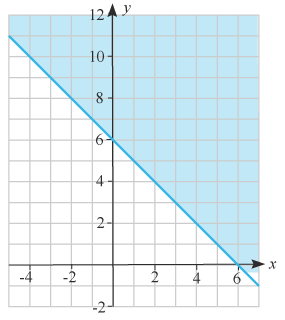 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Judith Lysell
Jag lyckas inte få rätt på fråga 3.
Varken y<2 eller y < 2 ger rätt.
Per Eriksson
Hej,
Mitt svar på fråga 2 accepterades inte fastän det var rätt. Det verkar inte som någon fått rätt på denna fråga. Kan ni göra svar till frågor som berör mindre än och större än tecken lättare att svara på?
Simon Rybrand (Moderator)
Hej
Den frågan är nu en flerval, fungerar den fortfarande inte?
Emma Lindh
Markeringen på axeln är inte korrekt när du ska beskriva olikheten −1< x ≤ 4 på en tallinje.
Simon Rybrand (Moderator)
Ja det hade blivit ett fel där, det är korrigerat!
Emelie Hagsmyr
När du går igenom olikheterna. Sista, -1 < x ≤ 4.
Då ska väl den ifyllda cirkeln vara på 4 och inte 3?
Eller tänker jag fel?
Emelie Hagsmyr
Måste ha råkat pausa precis på rätt tillfälle, då de är på fyra nu haha!
Joel Olsson
Tallinjerna som används i genomgången och frågeformuläret saknar talet 2. Ska det verkligen vara så?
Simon Rybrand (Moderator)
Hej, Nej tanken är inte att det skulle ha varit så. Vi får ordna den bilden. Tack för att du påpekade detta.
Endast Premium-användare kan kommentera.