Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Introduktion till sinussatsens två fall
En triangel där vi känner till en vinkel och två sidor kan i vissa fall konstrueras på två olika vis. Det tittade vi kort på i lektionen om areasatsen. När så är fallet så kan även sinussatsen ge två fall när man söker en sida eller en vinkel av satsen.
Sinussatsen
I en godtycklig triangel gäller följande samband mellan vinklar och deras motstående sidor.
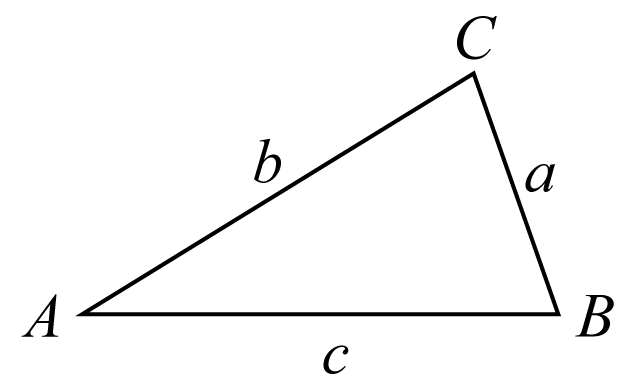
asinA=bsinB=csinCsinAa =sinBb =sinCc
Som vi nämnde i lektionen om sinussatsen kan man skriva om kvoterna till
sinAa=sinBb=sinCcasinA =bsinB =csinC
beroende på vilket som passar bäst för uppgiften man ska lösa. Tipset är att välja det samband som ger att en eventuell variabel hamnar i täljaren. Då slipper du lite jobb när du ska lösa ut den.
När ger sinussatsen två fall?
Som nämns ovan så kan sinussatsen ge två fall (lösningar) när vi känner till en vinkel och två av sidorna. Om vi exempelvis har triangeln ABC där vi känner till vinkeln A och sidorna a och b så kan denna triangel ritas ut på följande två vis.
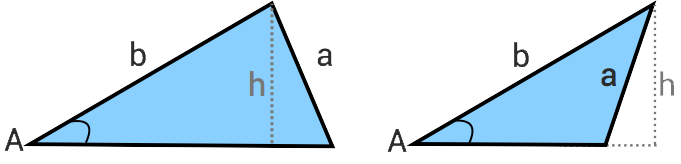
Det som gäller här är att vi har en spetsig vinkel A och den motstående sidan a som är mindre än sidan b och större än höjden h. Notera i figuren här ovan att det är sidan a som har flyttats (pendlats) så att ändpunkten längst ned är närmre vinkeln A. Längden på a har dock inte förändrats.
Alltså följande tre kriterier måste gälla för att vi skall få två lösningar:
- Vinkeln A är bestämd samt sidorna a och b. Däremot vet vi ingen annan vinkel eller sida.
- Vinkeln A är spetsig.
- h < a < b
Sinussatsen kan ge två fall
Nedan följer exempel där vi måste undersöka om sinussatsen kan ge två fall.
Exempel 1
Vi känner till följande om triangeln ABC:
Vinkeln A=35°A=35° och sidorna a=4a=4 och b=6b=6. Bestäm vinkeln BB.
Lösning
Vi kan skissa ut triangeln på följande två sätt
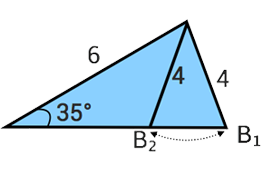
Vi tar då reda på B1B1 och B2B2 med hjälp av sinussatsen.
4sin35°=6sinBsin35°4 =sinB6
6⋅sin35°=4⋅sinB6·sin35°=4·sinB
sinB=sinB= 46⋅sin35°6·sin35°4
sinB≈0,86sinB≈0,86
Vi kan nu ta reda på vinkeln BB och de två fall som BB kan vara.
B1=sin−1(0,86)≈59,3°B1=sin−1(0,86)≈59,3°
B2=180∘−59,3°=120,7∘B2=180∘−59,3°=120,7∘
Olika typer av trianglar och antalet fall för dem
Nedan samlar vi i tabellform ett antal olika fall av trianglar som kan vara bra att kunna ta fram när du undersöker om en triangel kan ritas på inget, ett eller två sätt. hh motsvarar triangelns höjd mot basen.
| Vinkeln AA är spetsig (mindre än 90°90° ) | Vinkeln AA är trubbig (större än 90°90° ) | ||
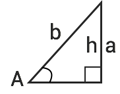 | 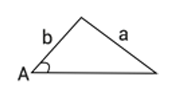 | 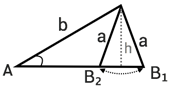 | 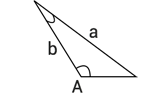 |
| a=ha=h | a≥ba≥b | hh < aa < bb | aa > bb |
Som följd av detta gäller att när a≤a≤hh kommer längderna inte kunna motsvara sidorna på en triangel.
Exempel 2
Undersök om det finns någon triangel ABCABC som uppfyller villkoren
AC=13AC=13 cm, BC=5BC=5 cm och vinkeln A=32∘A=32∘
Lösning
Vi börjar med att ta reda på vinkeln vid BB och för att göra det så använder vi sinussatsen.
13sinB=5sin32∘sinB13 =sin32∘5
sinB=sinB= 5sin32∘⋅13sin32∘·135
sinB=1,377…sinB=1,377…
Eftersom att sinus bara är definierat för värden mindre eller lika med ett, är detta inte möjligt.
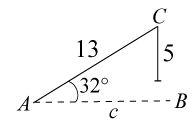
De givna värdena kommer ge att antingen är sidan BCBC för kort eller vinkeln AA för stor.
Genom att sätta in kända vinklar och längde i sinussatsen kan du nu bestämma okända sidor och vinklar även på trianglar som inte är rätvinkliga!
Kommentarer
e-uppgifter (4)
1.
(1/0/0)E C A B 1 P PL M R K Gabriella försöker rita en triangel med sidorna 100100 cm, 9595 cm och 44 cm men tycker att det är något som inte riktigt stämmer.
Går det att rita en sådan triangel?
Ange svaret med Ja eller Nej.
Svar:Ditt svar:Rätt svar: Nej(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B 1 P PL M R K Vilket samband stämmer för triangeln?
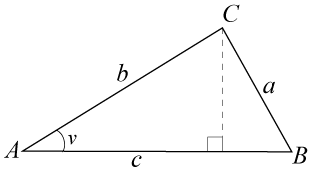 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K Vad krävs för att sinussatsen skall ge 2 fall/lösningar i följande triangel?
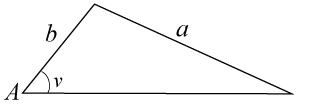 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm vinkeln v i figuren.

Avrunda ditt svar till en decimal.
Svar:Ditt svar:Rätt svar: 128,8°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (4)
5. Premium
(1/1/0)E C A B P 1 1 PL M R K 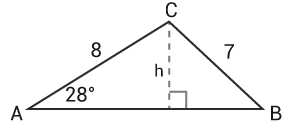
I triangeln ABC känner vi till att A=28∘A=28∘ och att AC=8AC=8 och BC=7BC=7.
Vilket är ett korrekt närmevärde av vinkeln BB ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/2/0)E C A B P 1 1 PL 1 M R K I triangeln ABC är A=28∘A=28∘ , AB=12,0 AB=12,0 cm och BC=10,0 BC=10,0 cm.
Bestäm den största möjliga vinkel som triangeln kan ha.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(0/1/0)E C A B P PL M R 1 K Undersök om det finns någon triangel ABCABC som uppfyller villkoren
AC=11AC=11 cm, BC=4BC=4 cm och vinkeln A=43∘A=43∘
Träna på att motivera ditt svar, men ange här Ja eller Nej.
Svar:Ditt svar:Rätt svar: Nej(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(0/2/0)E C A B P 1 PL 1 M R K 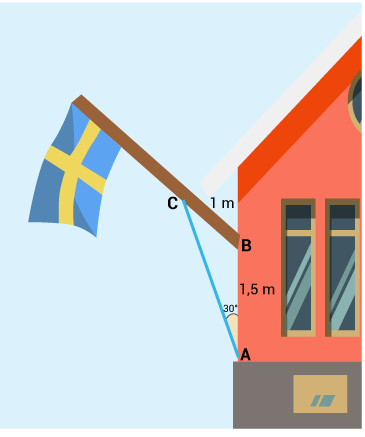
Peder och Viveka skall sätta upp en flaggstång på sin husvägg med hjälp av ett blått stag. Flaggstången skall vara vinklad uppåt så att vinkeln vid B är trubbig (se figur).
Avståndet A och B skall vara 1,5 1,5 m och avståndet mellan B och C skall vara 1,01,0 m.
Hur långt skall det blåa staget vara?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (2)
9. Premium
(0/0/3)E C A B P 1 PL 1 M R K 1 I triangeln T1T1 gäller att AC=4AC=4 och BC=3BC=3 samt att vinkeln A=30∘A=30∘.
I triangeln T2T2 gäller att AC=9AC=9 och BC=aBC=a samt att vinkeln B=30∘B=30∘.
Bestäm vinkeln AA i T2T2 så att T1T1 och T2T2 är likformiga.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(1/2/2)NPE C A B P PL 1 2 M R 1 K 1 Armand arbetar som silversmed och hans specialitet är smycken i form av olika geometriska figurer. Han har bestämt sig för att göra ett smycke i form av en triangel. Till sitt förfogande har han en 9,09,0 cm lång silvertråd som han kan böja och klippa.
Armand betecknar triangeln ABCABC och bestämmer sig för att vinkeln AA ska vara 30∘30∘, sidan ABAB 4,24,2 cm och sidan BCBC 3,23,2 cm.
Utred på vilket eller vilka sätt smycket kan utformas.
Vilka möjliga längder kan sidan ACAC anta?
Avrunda till en decimals noggrannhet.
Svar:Ditt svar:Rätt svar: 1,2 cm(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Johan Ahlberg
Jag får ut ett annat svar på A-uppgiften än det som står i förklaring.
Jag får att A1 ≈ 41,81 och att A2 ≈ 138,19.
I förklaringen avrundas det flera gånger genom hela uträkningen medans jag avrundade inte före jag skrev ett svar.
Hur kommer det sig att det avrundas flera gånger genom hela uträkningen, det verkar ju som att det påverkar svaret avsevärt.
Simon Rybrand (Moderator)
Om du siktar på ett så exakt svar som möjligt så avvaktar du med att ”slå ut” tex sin30 så länge som möjligt.
Ibland kan det dock vara enklare att slå ut det i delstegen för att följa uträkningen och inte få stora och kompakta uttryck.
Bägge sätten är möjliga i skolsammanhang, rör det sig om beräkningar i industrin är det förstås viktigt att vara så exakt som möjligt.
Abdullahi Mahamed
i första exemplet ska det va bc=8 inte 6 som ni löste det i lösningen.
Simon Rybrand (Moderator)
Tack för att du sade till om detta, vi fixar det.
Endast Premium-användare kan kommentera.