Författare: Simon Rybrand
Simon Rybrand  Anna Karp
Anna Karp
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Derivata är en funktion som anger förändringshastigheten hos en annan känd funktion. En funktions derivata beskriver hur mycket och i vilken riktning funktionens värde förändras då man rör sig från en given punkt.
Om exempelvis hastigheten för en bil beskrivs av funktionen $f\left(x\right)$ƒ (x) så motsvarar derivatan hur snabbt hastigheten förändras. Man kallar det förändringshastigheten. Det vill säga, derivatan beskriver bilens accelerationen $f’\left(x\right)$ƒ ’(x) vid en viss tidpunkt.
Vad ska man ha Derivatan till?
Genom att teckna matematiska modeller som beskriver verkliga skeende i världen kan man beräkna och analysera den. Vår samtid är nästan som besatt av att kunna mäta och analysera hur saker förändras. Ofta är syftet att genom vissa justeringar kunna maximera eller minimera olika skeenden. Intresset att försöka kunna förutse en utveckling eller kommande förändring alternativt studera förändringar för att kunna dra slutsatser kring hur olika saker påverkar varandra intresserar många. Av olika anledningar.

Inom matematiken är beräkningar av derivatan en metod att studera och beräkna funktioners förändringar. Derivatan är alltså en funktion, som anger förändringshastigheten hos en annan känd funktion. Eller med andra ord, en funktions derivata beskriver hur mycket funktionens värde förändras i en specifik punkt på grafen som tillhör funktionen.
Ett vanligt exempel för att beskriva derivatan är följande.
Exempel 1
Vi bestämmer att funktionen S(t)S(t)beskriver hur lång sträcka en bil färdats efter tt sekunder från att den startade. Då anger derivatan i de olika punkterna på grafen som tillhör funktionen S(t)S(t), vilken hastighet bilen har vid just en specifik tidpunkt under resan.
Derivatans funktionsvärde i sin tur, kan även undersökas med hjälp av det vi kommer att kalla för andraderivatan. Och denna kommer då motsvarar förändringshastigheten av hastigheten, det vi kallar för accelereration, när vi gasar bilen, och retardation, när vi bromsar bilen. Mer om detta i kommande lektioner.
I ett första skede fokuserar vi på förstaderivatan. Och den är alltså ett mått på förändring av funktionen i exemplet ovan med avseende på hastighet.
Exempel 2
Vi bestämmer att funktionen N(x)N(x) beskriver hur många invånare som bor i Kylarköping xx år efter år 20052005 . Då anger derivatan i de olika punkterna på grafen som tillhör funktionen N(x)N(x), förändringshastigheten just ett år, alltså med hur många personer per år antalet invånare ökar just xx år efter 20052005.
Olika betydelser av Derivatan
Vi kommer i kommande lektioner mer ingående beskriva hur man kan använda, beräkna och definiera derivatan. Men redan nu vill vi nämna några olika betydelser av derivatan som är bra att ha med sig för att underlätta förståelsen. Nämligen att derivatan är detsamma som värdet på tangenternas riktningskoefficienter som återfinns i olika punkter på grafen som tillhör funktionen. Den andra beskrivningen har vi redan nämnt, nämligen som en funktion som beskriver en annan funktions förändring. Vi sammanfattar här dessa betydelsen av derivatan.
Derivatans värde kan beskrivas som…
- kurvans lutning i en punkt, vilket är detsamma som tangentens lutning i punkten.
- förändringshastigheten i en punkt på kurvan.
Vi kommer utveckla dessa och även lägga till några ytterligare betydelser som underlättar arbetet med derivatan i kommande lektioner.
Derivatan som hjälp att analysera funktioner
Vi kommer i stor utsträckning använda derivatan för att fördjupa vår förståelse för funktioner och hur de förändras i olika punkter. Vi kommer med hjälp av derivatan enkelt kunna avgöra för vilka värden funktion antar sina största och minsta värden, vilket vi nämnde tidigare är önskvärt i samhället, för tillämpningen av matematiken.
Derivata är nära kopplat till verkliga händelser och situationer och har många användningsområden inom både Ekonomi, Natur-och Samhällsvetenskap.
Den vanligaste beteckningen för Derivatan
Det finns flera olika sätt att med matematiska symboler beteckna derivatan. Det vanligaste sättet är att markera funktionen man deriverar med en liten apostrof.
I exemplet vi presenterade tidigare, betecknade vi funktionen av sträckan SS med avseende på tiden tt för S(t)S(t). Derivatan till denna funktion skulle vi då kunna beteckna som S’(t)S’(t) . Vi utläser detta som ”s prim av t”.
f′(x)ƒ ’(x) uttalas ”f prim av x”.
Det vi då menar är förändringshastigheten av funktionen f(x)ƒ (x) i en viss punkt.
Andra beteckningar för Derivatan
Här kommer några andra skrivsätt för derivatan till funktionen y=f(x)y=ƒ (x) som också är ganska vanliga.
y’y’ y’(x)y’(x) dxdydydx dxdfdƒ dx Df(x)Dƒ (x) DyDy
Alla beteckningar här beskriver alltså samma sak, nämligen derivatan, vilket motsvarar förändringshastigheten i en viss tidpunkt.
- y’y’ uttalas ”y prim” och motsvarar derivatan av funktionen yy
- y′(x) uttalas ”y prim av x” och motsvarar derivatan av funktionen yy med avseende på variabeln xx
- dxdydydx uttalas ”d y d x” och motsvarar derivatan av funktionen yy avseende på variabeln xx
- dxdfdƒ dx uttalas ”d f d x” och motsvarar derivatan av funktionen fƒavseende på variabeln xx
- Df(x) uttalas ”derivatan av f(x)ƒ (x)” och motsvarar derivatan av funktionen f(x)ƒ (x) avseende på variabeln xx
- Dy uttalas ”derivatan av yy” och motsvarar derivatan av funktionen yy
Alla dessa sätt betecknar alltså samma sak, derivatan.
Exempel i videon
- Diskussion kring förändringen av en bils hastighet.
- Diskussion av förändringshastigheten i en punkt när en boll skjuts upp.
Kommentarer
e-uppgifter (7)
1.
(1/0/0)E C A B 1 P PL M R K Vilket av alternativen nedan beskriver derivatan?
Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Tangent och SekantRättar...2.
(1/0/0)E C A B 1 P PL M R K Vilket av följande alternativ är INTE en beteckning för derivatan?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K Vilket av alternativen nedan är INTE en beskrivning av derivatan?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K Vilket av alternativen nedan är INTE en korrekt tolkning av f’(x)ƒ ’(x) ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B 1 P PL M R K Vilket av följande alternativ kan man beräkna med derivatan?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B 1 P PL M R K När du gungar förflyttar du dig fram och tillbaka. När du gungar framåt har du en riktning och hastighet framåt. När du gungar bakåt har du en riktning och hastighet bakåt.
Men just i det ögonblick du byter riktning, så förflyttas du varken framåt eller bakåt och du har dessutom i detta ögonblick hastigheten noll.
Vad är derivatan i denna punkt?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(1/0/0)E C A B 1 P PL M R K 
När flygplanet startar stiger det högre och högre under 55 minuter. Vid en höjd på 10 00010 000 meter slutar planet att stiga och flyger sen en tid på samma höljd h(t)h(t) där tt motsvarar tiden från att planet startat.
Med vilken likhet kan vi beskriva planets förändringshastighet när det nått höjden 10 00010 000 meter?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (3)
8. Premium
(0/1/0)E C A B 1 P PL M R K En funktion N(t)N(t) beskriver hur många invånare det bor i en specifik stad, tt år efter 20002000 .
Vad beskriver likheten N′(5)=2000N´(5)=2000 ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...9. Premium
(1/1/0)ME C A B 1 1 P PL M R K Den räta linjen y=−2xy=−2x är en tangent till kurvan i punkten PP.
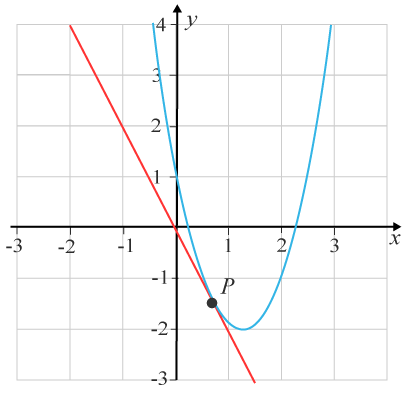
a) Bestäm tangentens lutning.
b) Bestäm kurvans lutning i punkten PP.
c) Bestäm derivatans värde i punkten PP.
Svar:Ditt svar:Rätt svar: a) −2 b) −2 c) −2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(0/2/0)E C A B 1 P PL M R 1 K 
En funktion h(t)h(t) beskriver hastigheten i m/s tt sekunder efter att en bil börjat bromsa.
Vad är ett rimligt värde på derivatan h′(x)h´(x) då t=1t=1, om bilens hastighet var 5050 m/s när den börjar bromsa?
Öva även på att motivera ditt svar.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Hans Elmehed
Hej!
Varför anger ni i videon med bollen att den har -2 m/s när den ökar sin hastighet på nervägen? När bilen bromsar in i ett annat exempel ger ju negativt värde, det är förståeligt.
Anna Admin (Moderator)
Det är lite lurigt ibland med hastighet. Man kan tänka att hastigheten även har en riktning. Alltså mer som en vektor. Det negativa värde innebär då att hastigheten är i motsatt riktning mot den ursprungliga riktningen.
Vill man bara veta hur snabbt, oberoende av åt vilket håll, kan man använda sig av absolutbeloppet som då bara anger storleken och inte om det är negativ eller positivt. Hoppas denna förklaring kunde ge dig lite klarhet.
Rasmus Mononen
Uppgift 7:
Om företaget redovisar vinst för verksamhetsåret 2013 med 600 000 SEK så har också själva vinsten skett under det verksamhetsåret. Inte sant? Det måste alltså vara under 2013 som ökningen sker. I uppgiftens facit står att vinsten skedde 2012. Möjligen menas att vinsten redovisas 2013 och att det gäller verksamhetsåret 2012 – men det måste nog i så fall beskrivas tydligare i uppgiften.
// Rasmus
V(2013)=600000
kronor – Ökningen var 500000
kronor.
Simon Rybrand (Moderator)
Vi kollar över den uppgiften, tack för din kommentar!
Tax
Hej! Om jag förstår derivatan rätt så kan man formulera det på följande vis: Derivatan är förändringshastigheten i en viss punkt. Det är även om vi skulle leka med uttrycket en slags medelhastighet ifall grafen skulle fortsätta i samma mönster som derivatans lutning? Ex. om vi har derivatan av X=1. Derivatan är 2 m/s i den punkten. Överallt längs tangentens räta linje är derivatan då om man kan uttrycka det så 2m/s? Alltså för varje X-led så ändras Y med 2 över hela tangentens linje.
Simon Rybrand (Moderator)
Hej
Det stämmer att derivatan är förändringshastigheten i en punkt. Det övriga resonemanget tycker jag är svårt att förstå vad du menar och att hålla med.
Michel Tosu
Hej,
övningsfråga 3 har ett felaktigt svar. Svarsalternativet stämmer inte överens med förklaringen.
Simon Rybrand (Moderator)
Tack för att du sade till om detta, vi har korrigerat det!
Julia Ojeda Ottosson
Har försökt lösa ovanstående uppgift men kommer inte fram till någon bra lösning. :/
Simon Rybrand (Moderator)
Är det funktionen f(x)=x22+2x=2x−2+2x? Den ser ut enligt följande:
Den har derivatan
f′(x)=−4x−3+2=x3−4+2
Löser ekvationen
f′(x)=0⇔
x3−4+2=0⇔
x3−4=−2⇔
−4=−2x3⇔
x3=2⇔
x=32
Julia Ojeda Ottosson
Hej! Min fråga är:
För funktionen f gäller att f(x)=2/x^2+2x
Lös ekvationen f´=0
Förstår ingenting, finns det någon genomgång angående detta?
Mvh Julia
Simon Rybrand (Moderator)
Hej, du kan kika på lite olika genomgångar som behandlar detta:
Derivera potensfunktioner
Derivata och nollställen
Hoppas att detta hjälper dig framåt!
Antigona Selaci
Någon som kan förklara hur man deriverar : x*(multiplicerat) roten ur x ?
och : 1/x^2-1/3 ?
Simon Rybrand (Moderator)
Hej
Kan visa den första där man kan skriva om funktionen med hjälp av potensregler så att det blir enklare att derivera.
y=x⋅x=x⋅x1/2=x1+1/2=x3/2
y′=23⋅x1/2=23x
Eric
Kanonbra! Fick en lättare syn på derivata nu
johannawallstrom
Hej!
Vill bara tacka för dessa genomgångar!! Jag klarade att på egen hand tenta av ma3b, och har nu kommit in på Lantmätarprogrammet! Tuuusen tack!!!!!!!!!!!!!! /Johanna-som hatade matte innan
Simon Rybrand (Moderator)
Stort grattis till att du kom in på din utbildning!
Kul att du har haft hjälp av oss!
daniel
inte illa . inte börjat gymnasiet än men förstod ändå innebörden . bra förklarat !
nti_ma3
Svaret på fråga 3 borde väl vara h′(x)≤0. Bilen skulle ju kunna ha kört så sakta att den står still efter tex. 0,98 sekunder.
Simon Rybrand (Moderator)
Hej, helt rätt att det kan vara så. Har ändrat i uppgiften där så att den inte skall misstolkas, tack för din kommentar.
Peter
Tack för en bra förklaring av derivata, tror jag förstår bättre nu vad detta egentligen betyder, nu skall jag ta tag i deriveringsreglerna också… 😉
Simon Rybrand (Moderator)
Hej Peter och tack för uppskattningen. Om du väl förstår grunderna i derivata och vad begreppet innebär så kommer det att bli enklare att komma igång med deriveringsreglerna, om du har konto hos oss så hittar du genomgång på derivatans definition här och första genomgången på deriveringsregler här.
Endast Premium-användare kan kommentera.