Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Kontinuerliga funktioner
I introduktionslektionen om kontinuerliga funktioner sa vi att man förenklat kan säga, att den kontinuerlig funktionens graf går att rita utan att lyfta pennan från papperet. Som en grov förklaring av de kontinuerliga funktionerna kan detta var till hjälp. Men vi sa även att det kan lura oss lite. Även en funktion som vi måste lyfta på pennan för att kunna rita, kan vara kontinuerlig. Detta gäller exempelvis för alla diskreta- och rationella funktioner. Vi ska här ge en fördjupad definition av kontinuerliga funktioner.
Definition av kontinuerliga funktioner
En funktion y=f(x)y=ƒ (x) är en kontinuerlig funktion om den är kontinuerlig i varje punkt i sin definitionsmängd.
Det innebär att en funktion kan vara kontinuerlig i sina olika definierade intervall, även om det finns avbrott i definitionsmängden, vilket kan ge upphov till ”glapp” i grafen. Ett exempel på detta är funktioner som rationella uttryck där nämnaren gör att funktionen inte är definierad för vissa värden för xx.
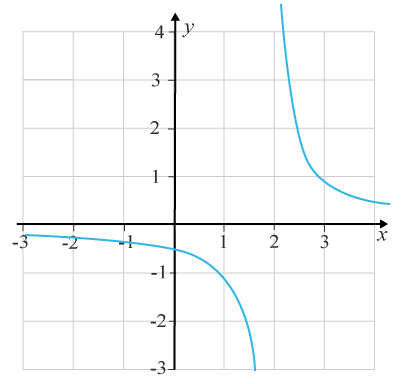
Vi har här funktionen f(x)=ƒ (x)= (x−3)11(x−3) +4+4
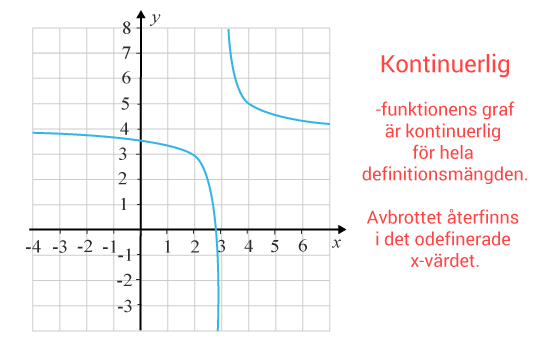
Vi ser att man måste lyfta penna då x=3x=3 för att kunna rita grafen. Men efter som att funktionen inte är definierad för detta xx -värde, så är ändå funktionen kontinuerlig, sammanhängande, i sina definierade intervall, x>3x>3 och xx<3<3. Funktionen uppfyller alltså definitionen för en kontinuerlig funktion.
Däremot är funktionen inte kontinuerlig i punkten x=3x=3 eftersom att den inte har samma funktionsvärde om man närmar sig punkten från höger eller vänster. Från höger går funktionens värde mot positiv oändlighet och från vänster mot den negativa oändligheten.
Vi definierar kontinuitet i en icke-isolerad punkt aa i en definitionsmängd på följande vis med hjälp av gränsvärden. Du kommer få lära dig om gränsvärden i kommande lektioner, men här visar vi bara skrivsättet.
En funktion fƒ är kontinuerlig i x=a om
x→a+limf(x)=x→a−limf(x)=f(a)
Definitionen innebär att oavsett om man närmar sig f(a)ƒ (a) från höger eller vänster längs grafen, så ska funktionsvärdet, om funktionen är kontinuerlig i punkten, närma sig samma funktionsvärde från båda hållen.
Så man får tänka ett varv till, innan man lätt avfärdar alla funktioner med avbrott som diskontinuerliga.
Kontinuerlig och Diskontinuerlig
Observera att det två egenskaperna kontinuerlig och diskret inte är varandras motsatser, utan motsatsen till kontinuerlig är diskontinuerlig.
Värdemängden avgör om en funktion är kontinuerlig. Man säger följande.
En funktion fƒ är kontinuerlig då den är kontinuerlig i varje punkt i sin definitionsmängd.
Grafen till en kontinuerlig funktion gör därmed inga ”språng” eller ”glapp” för xx som tillhör definitionsmängden. Nedan ser vi grafen till en diskontinuerlig funktion med definitionsmängden −3≤−3≤x≤6x≤6.
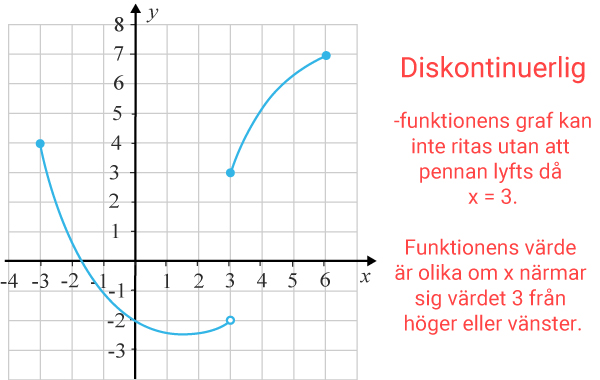
Diskontinuiteten uppstår i x=3x=3 eftersom att f(3)ƒ (3) när vi närmar oss från vänster närmar sig −2−2 och från höger 33, alltså olika funktionsvärden.
Däremot kan den ha ”språng” för xx-värden som inte tillhör definitionsmängden utan att för den del vara diskontinuerlig. Nedan ser vi grafen till en kontinuerlig funktion med definitionsmängden x=3x≠3 i intervallet −3≤−3≤ x≤6x≤6.
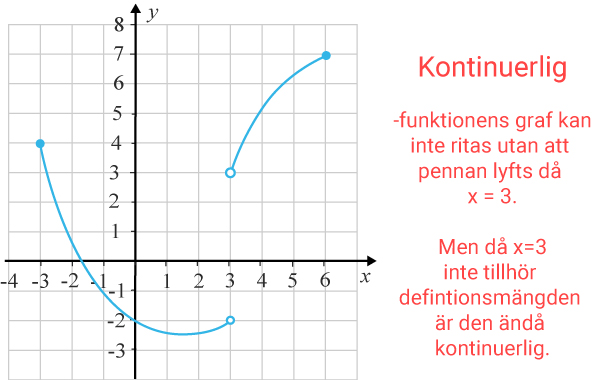
Vidare är det definitionsmängden som avgör om en funktion är diskret. Är definitionsmängden diskret, alltså endast bestående av isolerade punkter, leder det till grafen kommer innehålla ”glapp” och därmed inte är kontinuerlig.
Exempel 1
Grafen tillhör funktionen y=floor(x)y=ƒ loor(x) där xx tillhör det reella talen i intervallet 0≤0≤ x<7x<7.
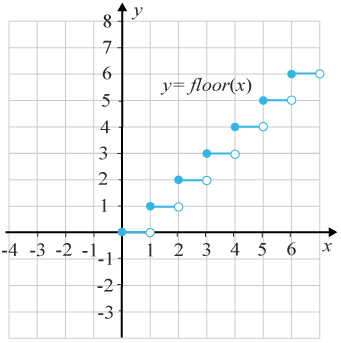
a) Är funktionen med ovanstående graf kontinuerlig?
b) Är funktionen med ovanstående graf diskret?
Lösning
a) Funktionen är inte kontinuerligt, eftersom att om vi rör oss mot exempelvis x=2x=2 från höger eller från vänster ges olika gränsvärden för f(2)ƒ (2). Vi får att
x→2−limf(x)=1
och
x→2+limf(x) =2
vilket leder till att
x→2+limf(x)=x→2−limf(x)
Liknande diskontinuitet uppstår för varje heltal i intervallet 1≤1≤ x≤6x≤6.
b) Om definitionsmängden är diskret är den åtskild. Funktionen är därför inte diskret, eftersom definitionsmängden är sammanhängande. Funktionen är definierad för alla reella xx-värden från och med noll upptill sju och omfattar inte isolerade punkter.
Utvidgad kontinuitet
För att kunna motivera att en rationell funktion är kontinuerlig kan vi använda oss av en så kallad utvidgad kontinuitet. Det kan vi göra men hjälp av gränsvärdesberäkningar. Mer om detta i lektionen om gränsvärden.
Kontinuitet och deriverbarhet
I kommande lektioner kommer vi att introducera ett nytt begrepp som kallas för derivatan. Med derivatan kan vi beskriva förändringshastigheten i en funktions olika punkter.
För att kunna ange derivatan i en specifik punkt i funktionen måste den vara kontinuerlig. Därför gäller följande.
Om en funktion fƒ är deriverbar i x=ax=a så är även fƒ kontinuerlig i x=ax=a
Grafen till en kontinuerlig funktion är sammanhängande i hela sin definitionsmängd. Grafen till en deriverbar funktion är dessutom ”mjukt” sammanhängande. Det vill säga, grafen gör inga tvära byten i riktning. Exempelvis är funktionen f(x)=∣x∣ƒ (x)=|x| konturering men inte deriverbar i x=0x=0. För grafen byter riktning plötsligt kring origo. Det ger att den inte är ”tillräckligt mjuk” för att kunna dra en entydig tangent i origo.
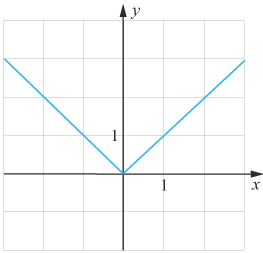
Men mer om det i lektionen om växande och avtagande funktioner.
Exempel i videon
- Ange definitionsmängd, avgör om f(x)ƒ (x) är kontinuerlig samt skissa kurvan till f(x)=x1ƒ (x)=1x .
Kommentarer
e-uppgifter (7)
1.
(1/0/0)E C A B 1 P PL M R K Är funktionen med följande graf kontinuerlig?
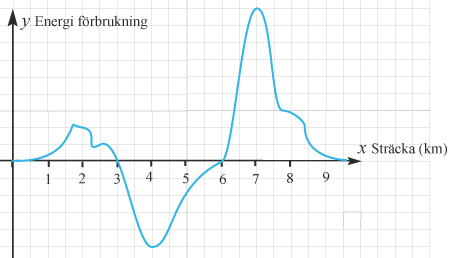
Svara med Ja eller Nej.
Svar:Ditt svar:Rätt svar: Ja.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B 1 P PL M R K Är funktionen med följande graf kontinuerlig?
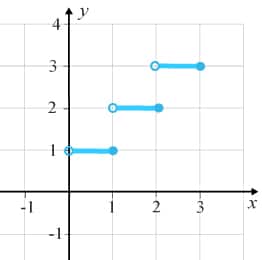
Svara med Ja eller Nej.
Svar:Ditt svar:Rätt svar: Nej.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K Är funktionen med följande graf kontinuerlig?

Svara med Ja eller Nej.
Svar:Ditt svar:Rätt svar: Ja.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K Vilken är värdemängden för funktionen y=x2−9y=x2−9 då definitionsmängden är alla reella tal RR ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(2/0/0)E C A B 1 P 1 PL M R K Frågan ingå i Ma3c.
Är funktionen f(x)=∣2x−1∣ƒ (x)=|2x−1| deriverbar för alla xx ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B 1 P PL M R K Fråga ingår i Ma3c.
Figuren visar grafen till en funktion. Är funktionen deriverbar för alla xx?
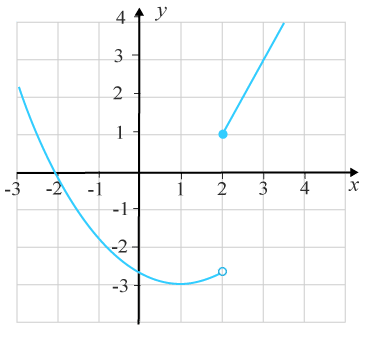
Välj det alternativ du anser stämmer bäst.Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(1/0/0)E C A B 1 P PL M R K Fråga ingår i Ma3c.
Figuren visar grafen till en funktion. Är funktionen deriverbar för alla xx?
Välj det alternativ du anser stämmer bäst.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (2)
8. Premium
(0/1/0)E C A B 1 P PL M R K Vilken är defintionsmängden för f(x)=4−xƒ (x)=√4−x ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...9. Premium
(0/2/0)E C A B P PL M 1 R 1 K Skissa grafen till funktionen f(x)=ƒ (x)=2−x112−x för hand, genom att först beräkna funktionsvärdet för väldigt stora och små xx -värden.
Är funktionen kontinuerlig?
Svar:Ditt svar:Rätt svar: Ja, funktionen är kontinuerlig(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (1)
10. Premium
(0/0/2)E C A B P PL 1 M R K 1 För vilket värde på aa är funktionen f(x)ƒ (x) inte kontinuerlig?
f(x)=ƒ (x)= (a2−4a)x2−ax+9x2−ax+9(a2−4a)
Svara på formen ”a=siffra och a=siffra”
Svar:Ditt svar:Rätt svar: a1=0 och a2=4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Hans-Christian Karlsborn
I fråga 5 undrar jag om grafen som utritas i förklaringen verkligen är korrekt? f(x)=2x-1
jag får det till att alla värden mindre än 0,5 blir negativa. Vad är det jag missar?
Freja Sjöqvist
Hej, om det står att frågan ingår i matte 3c men jag pluggar för matte 3b, ska jag då hoppa över den frågan eller varför kommer det upp?
Anna Eddler Redaktör (Moderator)
Exakt så. #c är lite mer fördjupande än 3b.
Evelina Persson
Hej, i sista frågan blir det en bugg i formeln och vi förstår inte på grund av dollartecknet.
Anna Admin (Moderator)
Hej Evelina, tack för att du uppmärksammade oss på detta. Det är nu korrigerat.
Lycka till med funktionerna!
Asha Ahmed
Jag skrev a=0,a=4 och det är rätt svar, så varför står det fel?
Endast Premium-användare kan kommentera.