Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1b
/ Funktioner
Definitionsmängd och Värdemängd
När man jobbar med funktioner är två viktiga begrepp att känna till definitionsmängd och värdemängd. I den här lektionen presenterar och fördjupar vi oss i begreppen.
Eftersom detta hänger tätt i ihop med funktionsläran, tar vi några konkreta exempel utifrån några funktioner.
Definitionsmängd
Begreppet definitionsmängd motsvarar alla värden som för funktionen är tillåtna för den oberoende variabel, ofta $x$x. Eller med andra ord, de $x$x-värden som är förutbestämda på något sätt eller gör det möjligt att beräkna ett tillhörande funktionsvärde.
Vilka $x$x-värden som är tillåtna varierar från funktion till funktion.
Ett exempel skulle kunna vara att man i grundläggande geometriska sammanhang bara ”tillåter” $x$x-värden som är större än noll. Det beror på att vi sällan pratar om längder, areor eller volymer som är negativa.
Man kan definiera en definitionsmängd som
Alla tillåtna invärden för funktionen.
Som sagt motsvarar dessa invärden den oberoende variabeln, vilka oftast betecknas med variabeln $x$x.
Låt oss ta ett exempel för att göra detta mer tydligt.
Exempel 1
I koordinatsystemet är funktionen $y=f(x) $ utritad. Ange funktionens definitionsmängd.
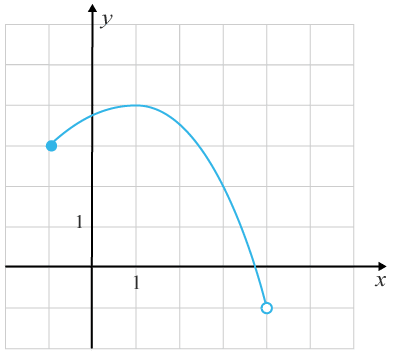
Lösning
Definitionsmängden motsvarar alla tillåtna $x$x -värden. Alltså alla värden på $x$x som återfinns på grafen. Vi har en ifylld punkt där $x=-1$x=−1 och en tom punkt i $x=4$x=4. Det ger att den nedre intervallgränsen är stängd och den övre öppen.
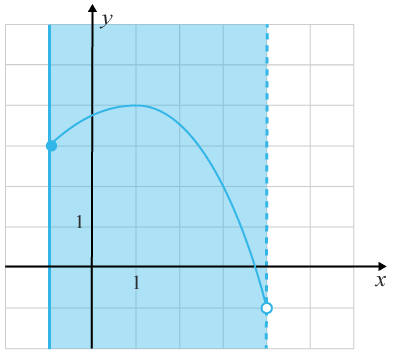
Vi får då att definitionsmängden motsvarar intervallet $-1\le$−1≤ $x<4$x<4.
Värdemängden
Begreppet värdemängd motsvarar alla värden som blir givna, eller erhålls, utifrån funktionsuttrycket och den oberoende variabel. Värdemängden motsvarar alltså funktionsvärdena och betecknas ofta med variabeln $y$y. Eller med andra ord, värdemängden är de $y$y -värden som tillhör funktionen utifrån definitionsmängden.
Ett exempel utifrån tidigare resonemang skulle kunna vara att man i grundläggande geometriska sammanhang bara erhålla funktionsvärden som är större än noll, eftersom att vi som sagt sällan pratar om sig längder, areor eller volymer som är negativa.
Man kan definiera en värdemängd som
Alla erhållna, eller givna, utvärden för funktionen.
Som sagt motsvarar dessa utvärden den beroende variabeln, vilka oftast betecknas med variabeln $y$y.
Exempel 2
I koordinatsystemet är funktionen $y=f\left(x\right)$y=ƒ (x) utritad.Ange funktionens värdemängd.
Lösning
Värdemängden motsvarar alla givna funktionsvärden utifrån definitionsmängden. Med andra ord, alla $y$y-värden som finns på grafen. Vi har en tom punkt i $y=-1$y=−1. Det betyder att $y$y inte antar värdet minus ett, även om det kan komma hur nära värdet som helst. Det ger att den nedre intervallgränsen är öppen.
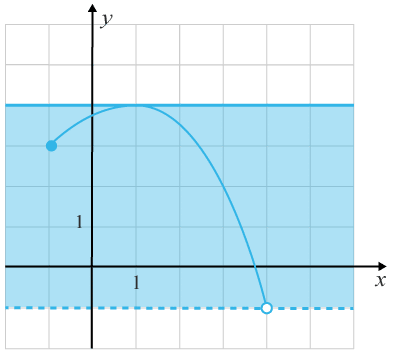
Vidare har vi en ifylld punkt där $y=3$y=3. Men eftersom att funktionen även går ovanför $y=3$y=3 har vi större funktionsvärden som också tillhör funktionen. Alla punkter på grafen tillhör funktionen och vi läser av att det största funktionsvärdet är när $x=1$x=1 och motsvarar värdet $y=4$y=4 . Eftersom att funktionsvärdet fyra är en del av funktionen, ger det att den övre intervallgränsen är stängt, eller slutet, som man också kan säga.
Vi får då att värdemängden motsvarar intervallet $-1<$−1< $y\le4$y≤4 .
Exempel i videon
- Definitionsmängd och värdemängd för en utritad funktion i ett koordinatsystem.
- En rektangulär kohage förhåller sig enligt vissa dimensioner utritade i en figur. Bestäm en funktion som beskriver arean samt definitionsmängd och värdemängd för funktionen.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (8)
-
1. Premium
Funktionen $p(x)$p(x) beskriver hur ett barn växer fram till och med att det är $18$18 år gammal, där $p$p är längd och $x$x är åldern. Vilken är definitionsmängden för funktionen?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
Ange definitionsmängden för funktionen som är utritad i figuren.
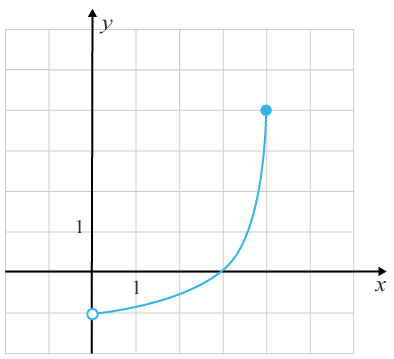Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
Ange värdemängden för funktionen som är utritad i figuren.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
Ange definitionsmängden för funktionen som är utritad i figuren.
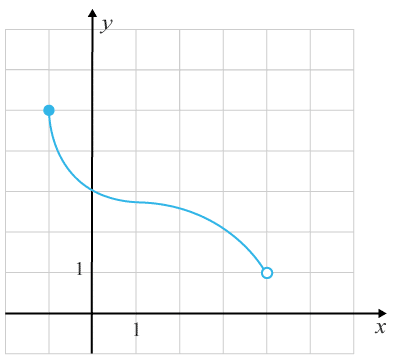Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
5. Premium
Ange värdemängden för funktionen som är utritad i figuren.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Definitionsmängd och Värdemängd funktion Funktioner Linjära funktioner Matematik 1 Matematik 2 värdemängdRättar... -
6. Premium
Ange värdemängden för funktionen som är utritad i figuren.
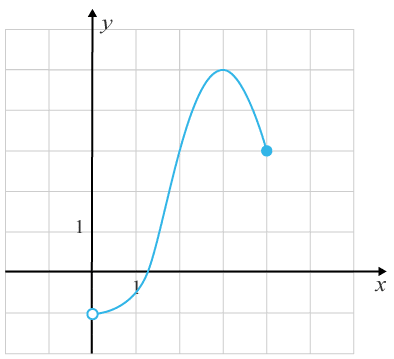Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Definitionsmängd och Värdemängd funktion Funktioner Linjära funktioner Matematik 1 Matematik 2 värdemängdRättar... -
7. Premium
Funktionen $f(x)=15x$ƒ (x)=15x har definitionsmängden $0\le$0≤ $x\le100$x≤100.
Ange funktionens värdemängd.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
8. Premium
Funktionen $f(x)=10x-10$ƒ (x)=10x−10 har värdemängden $0\le y\le100$0≤y≤100.
Vilken definitionsmängd har funktionen?Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
c-uppgifter (9)
-
9. Premium
En triangel har ett hörn med vinkeln $30$30 grader. De andra hörnen är märkta som $x$x och $y$y. Om $y$y är en funktion som beror på $x$x, vilken är då funktionens definitionsmängd?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
10. Premium
I ett koordinatsystem finns en rät linje som skär $x$x-axeln i $x=3$x=3. Linjen är parallell med $y$y-axeln.
Är linjen en funktion?
Ange svaret Ja eller Nej, men träna även på att motivera ditt svar.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: begrepp definition funktion Funktioner x=aRättar...11. Premium
En hyrbil kostar $540$540 kr att hyra per dygn. För det priset får du köra $100$100 km. Om du kör en längre sträcka, tillkommer en kostnad på $3,50$3,50 kr per km.
Ange värdemängden som motsvarar kostnaden för att hyra bilen ett dygn om du kör maximalt $500$500 km.
Kommer den totala kostnaden understiga $2\text{ }000$2 000 kr?
Ange svaret med Ja eller Nej, men träna även på att motivera ditt svar.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: linjära modell problemlösning värdemängdRättar...12. Premium
Ange värdemängden för funktionen $f(x)=$ƒ (x)= $\frac{1}{x}$1x .
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Definitionsmängd och Värdemängd funktion Funktioner Linjära funktioner Matematik 1 Matematik 2 värdemängdRättar...13. Premium
Ange definitionsmängden för funktionen $f(x)=$ƒ (x)= $\frac{1}{x}$1x .
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: definitionsmängd funktion Funktioner Linjära funktionerRättar...14. Premium
Ange för vilket eller vilka värden funktionen $f(x)=$ƒ (x)=$\frac{1}{3+x}$13+x inte är definierad.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: definitionsmängd Funktioner rationellt uttryck värdemängdRättar...15. Premium
Ange definitionsmängden för funktionen $y=$y= $\frac{5}{x^2+1}$5x2+1 .
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: definitionsmängd Definitionsmängd och Värdemängd Funktioner Linjära funktioner Matematik 1 Matematik 2Rättar...16. Premium
Ange definitionsmängden för funktionen $y=\sqrt{x}$y=√x
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: definitionsmängd Definitionsmängd och Värdemängd Funktioner Linjära funktioner Matematik 1 Matematik 2Rättar...17. Premium
Vad är definitionsmängden för funktionen $f(x)=$ƒ (x)= $\frac{x}{g(x)}$xg(x) om $g(x)=x-1$g(x)=x−1 ?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Beteckningen f(x)Liknande uppgifter: Beteckningen f(x) f(x) funktion Funktioner Linjära funktioner Matematik 1 Matematik 2Rättar...a-uppgifter (1)
-
18. Premium
I koordinatsystemet är grafen till en funktion utritad. Bestäm med hjälp av grafen för vilka värden på $x$x olikheten $y\ge4$y≥4 gäller.
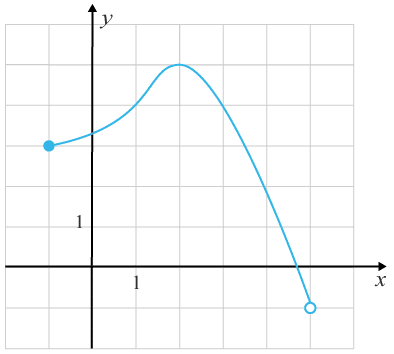Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
-
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
Tina Westring
I areaexemplet i videon så är det största värdet (värdemängd) som x kan anta lika med 5.
Varför är det så?
Simon Rybrand (Moderator)
Hej, rent generellt blir arean för en rektangel alltid störst då rektangeln är kvadratisk.
Du kan också rita ut funktionen $A(x)=10x-x^2$ och då ser du att det största y-värdet kommer att vara 25 då x=5.
Moa Degerfält
Hej, tack för bra videos!
På första uppgiften svarade jag rätt enligt förklaringen men fick fel på uppgiften. Det finns inte heller utmarkerat vilket som skulle vara rätt. måste vara et litet fel bara.
Adrian Vodovozov
Vad menas med olikheten?
Simon Rybrand (Moderator)
En likhet skrivs med symbolen ”=” tex att $3x = 3$, dvs att $x=1$
Vid en olikhet så används istället symbolerna ”<", ">”, ”≤” och ”≥”.
Så om tex $3x>3$ (3x är större än 3) så gäller att $x>1$
RedEagle
Hej,
Det har skett ett skrivfel i texten till den första grafen, det står def. mängden är −2≤x<2, men det ska väl vara −3≤x<2?
Simon Rybrand (Moderator)
Texten är korrigerad, tack för att du sade till!
mdnaziri@hotmail.com
Hur visste du att värdemängden skulle vara 25? Tack!
Simon Rybrand (Moderator)
Hej,
Titta på mitt svar här ovanför, där länkar jag till två stycken kommentarer där jag svarar på just detta. Om du ändå inte förstår så säg till så tar vi det därifrån!
mdnaziri@hotmail.com
Jag förstod inte riktigt, hur fick man fram att det största värdet y kunde få är x=5? Tack!
Simon Rybrand (Moderator)
Hej
Denna fråga har dykt upp tidigare och besvarats så kika gärna svaret till följande två kommentarer:
Kommentar 1
Kommentar 2
Om du fortfarande inte förstår så säg till så tar vi det därifrån!
Henrik F
Hej! I fråga 6. står det denna förklaring till det rätta svaret:
Eftersom vinkelsumman i en triangel är 180 grader så kommer vi ha en övre gräns på hur stora x och y kan vara. y ska vara en funktion beroende på x, dvs y=180−30−x=150−x. En vinkel kan inte vara noll eller större än 150 enligt formeln, så därför blir definitionsmängden 0<x<150
Vad jag inte får ihop är att 0<x<150 inte finns som alternativ, utan 0<x<145 är markerat som rätt svar.
Simon Rybrand (Moderator)
Hej
Nej det var fel i det alternativet, det är korrigerat. Tack för att du påpekade detta.
gul
Tack så mycket men hur man räknar ut mängdvärden för att bevisa att h: funktion är ej surjektiv?
gul
hej
jag har fråga om värdemämng, definitionmängd och målmäng. sammasatta två funktion
f(a)=1/4 cos(pia)-2 f:A ⇔ B
g(a)=-2a/3 g:C ⇔ A
h(a)=f(g(a))
å blir h(a)=1/4 cos(pi(-2a/3))-2
frågan är att bestäm h:s definitionmäng och målmängd och värdemängden.
kan ni hjälpa mig med detta frågan? jag fasnade detta frågan:
Simon Rybrand (Moderator)
Hej
Om jag tolkar din fråga rätt här så bör Definitionsmängden för $\frac{1}{4}\cos \left(\pi \left(\frac{\left(-2x\right)}{3}\right)\right)$ vara alla x och värdemängen ligger i intervallet $ -0,25 ≤ y ≤ 0,25 $. Avläste detta genom att rita ut denna graf. Eftersom att värdemängden består att alla reella tal inom intervallet så kan målmängden sägas vara alla reella tal. Hoppas att detta hjälper dig vidare!
angela zetterlund
Är målmängden alla reella tal? Jag undrar över om hur begreppet värdemängd hänger ihop med begreppen utfallsrum och begreppen outputvärden.
Simon Rybrand (Moderator)
Hej
Alla erhållna y-värden, dvs värdemängden, är en del av den så kalla målmängden. Man kan säga att värdemängden är en delmängd till målmängden.
Om du för en funktion y=f(x) exempelvis har värdemängden {1,2,3,4} så är kan målmängden sägas vara de naturliga talen. Värdemängden är då en delmängd av de naturliga talen.
Utfallsrum är framförallt ett begrepp som används inom sannolikhetslära, i vilket sammanhang har du hört det kring funktionslära?
auroralexx
Hej!
Funderingar över uppgift 5.
Rätt svar är S0 säger den… Men sen när den förklarar varför det är rätt så säger den 0 < x < 18. Antar att det har blivit nå fel i htmlkoden eller så?
—————————–
Samt så förstår jag inte riktigt uppgift 6:
"I en triangel har ett hörn vinkeln 30 grader. De andra hörnen är märkta som x och y. Låt y vara en funktion som beror på x, vad är då dess definitionsmängd?"
Jag skulle få det till 180 – 30 = 150, och därav svaret: 0 < x < 150.
I förklaringen säger den helt plötsligt 35 och att svaret är 0 < x < 145? Vart kom 35 ifrån?
Simon Rybrand (Moderator)
Hej
Ja det ha blivit ett fel vid kodningen där, det är korrigerat. Tack för att du kommenterade detta.
Ki Nyhlen
Nu står det 30 i frågan och 145(35) i svaret på uppgift 6 istället.
Mvh
Ki
Simon Rybrand (Moderator)
Fixat, tack för att du sade till!
thorus
I fråga nummer tre så står det följande i förklaringen:
”Alltså är värdemängden 15 ≤ y ≤ 100”
Men det alternativet som blir grönmarkerat är: 0 ≤ y ≤ 1500.
Simon Rybrand (Moderator)
Det var fel i förklaringen där, det är korrigerat. Tack för att du sade till om detta.
amanda koziol
Är inte koordiatsystemet omkring 4 minuter in i videon felaktigt? De positiva y-värdena stämmer inte, 2 fattas och ”stegen” är inte lika stora!
Simon Rybrand (Moderator)
Hej,
Den här videon kommer att uppdateras inom kort då det har varit många frågor kring en uppgift samt att koordinatsystemet i bilden skall fixas till. Tack för att du påpekade detta.
thronell
Jag har läst igenom tidigare inlägg, men jag förstår fortfarande inte vart 5 och 25 kommer ifrån. Går det att förklara ännu enklare tro?
Simon Rybrand (Moderator)
Hej, jag har förstått att många tycker att detta är klurigt 🙂
Du söker ju det x-värde som ger det största y-värdet i intervallet. Jag tror att du behöver förstå hur själva grafen till funktionen $y=10x-x^2$ ser ut och att denna är symmetrisk (se bild i kommentar här ovan) kring $x=5$. Dvs det till vänster är en spegelbild av det till höger om om symmetrilinjen i $x=5$ (och vice versa). Det största värdet för en sådan andragradsfunktion är alltid i symmetrilinjen om vi har en negativ $x^2$ term.
Johan Bergquist
Hej!
Man kan inte få ett till exempel på värde mängden för Kohagen men med en annan area tex om 10<x<1000? Ska man generellt sätt alltid leta sig till mitten av definitions mängden ex 10<x<1000 för att få den största värdemängden?
Simon Rybrand (Moderator)
Hej,
Ja ofta så ligger det största värdet på värdemängden ”i mitten” eller i symmetrilinjen om man ritar ut andragradsfunktionen som har en maximipunkt mitt emellan nollställena. Det som skulle kunna vara värt att hålla koll på är om definitionsmängden har ett intervall där denna maximipunkt inte ingår. Viktigt är då att startpunkten eller slutpunkten ingår i intervallet.
Exempelvis om vi tar kohageexemplet och säger att definitionsmängden är $0 < x ≤ 2$ så kommer ju det största värdet att finnas i $x=2$. Hoppas att det här resonemanget hjälper dig!
Alex Park
Nu hänger jag med 🙂
Tack för feedback! Grym sida! Ett jätte verktyg ni har skapat för oss som läser på distans!
Alex Park
Hej,
i videolektionen där i slutet säger du att max värdemängd blir = 25,
Hur får du fram att x=5 är det största värdet? 0≤x<10
Simon Rybrand (Moderator)
Hej, se svaret på kommentaren här ovan, där resonerar jag kring detta. Om det inte hjälper så fråga gärna igen så tar vi det därifrån.
Ash Raf
jag fattar inte var kommer 5 och 25 från i den sista uppgift?
Simon Rybrand (Moderator)
Hej,
Enkelt uttryckt gäller att arean är störst när bredden och längden är lika stora, dvs då $x=5$.
Men om man fördjupar det lite så kan man fundera på vilket det största värdet för funktionen $ y=10x-x^2 $ är? Det värdet hittar vi mitt emellan nollställena. Så om vi tar reda på nollställena så är dessa
$ x(10-x)=0 $
$ x_1=0 $ och $ x_2=10 $
x-värdet mitt emellan dessa nollställen är alltså $ x=5 $ och det är där vi får vårt största värde på $y$, dvs $y=25$.
Hoppas att förklaringen hjälper!
Lien Tran
Hej
Hur räknar jag ut sidorna på rektangel om jag har formen
x.(2x+3)= 65. I facit står svaret x1= 5 och x2= 13. Skulle du kunna visa mig steg för steg?
MVH
Lien
Simon Rybrand (Moderator)
Nu har jag ju inte uppgiften framför mig men jag antar att den ena sidan är $x$ och den andra är $(2x+3)$ och att arean är 65?
Då har du ekvationen
$x(2x+3)=65 \Leftrightarrow$
$2x^2+3x-65=0 \Leftrightarrow$
$x^2+\frac32x-\frac{65}{2}=0 \Leftrightarrow$
$x=-\frac34\pm\sqrt{\frac{9}{16}+\frac{65}{2}} \Leftrightarrow$
$x=-\frac34\pm\sqrt{\frac{9}{16}+\frac{520}{16}} \Leftrightarrow$
$x=-\frac34\pm\sqrt{\frac{529}{16}} \Leftrightarrow$
$x=-\frac34\pm\frac{23}{4} $
$ x_1=5 $
$ x_2=-\frac{13}{2} $
$ x_2 $ är inte ett möjligt svar så den ena sidan är $5$ och den andra blir då $2\cdot5+3=13$
carinaa
hur beräknar man definitionsvärdet på en cirkel?
Simon Rybrand (Moderator)
Hej
Det beror ju lite på vad som är den så kallade oberoende variabeln för cirkeln och vad det är du skall beräkna, är det t.ex. omkrets eller area?
Om du exempelvis har en areafunktion för cirkeln där den oberoende variabeln är radien,
$ A(r) = \pi r^2 $
så är de tillåtna värdena för radien definitionsmängden.
yvonne van klaveren
I videon med kohage står: det största värdet ges då x=5, varifrån kommer då 5????
Yvonne
Simon Rybrand (Moderator)
Hej Yvonne,
När det gäller rektanglar där sidorna hänger samman på det vis som beskrivs i uppgiften så kommer du få störst area när sidorna är lika långa, dvs 5m. Då har vi också en kvadrat (som också är en rektangel).
Vi skulle kunna utveckla det en aning genom att titta på areafunktionen:
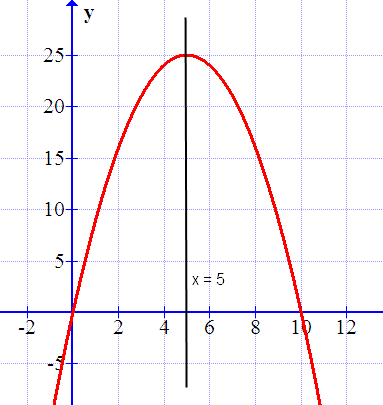
$ A(x) = 10x – x^2 $
Vi ritar ut den i en graf:
Här ser vi att linjen x = 5 som också kallas för symmetrilinje går genom areafunktionens högsta punkt.
tjarnbro
Stämmer första genomgången av värdemängden? Blir lite förvirrad av att man ska läsa av y-värdet på y-axeln, men det står att ”x är större eller lika med -1.5”
Är jag trög värre än vanligt? 🙂
Simon Rybrand (Moderator)
Nej det är så att det smugit sig in ett fel i texten där. Videon är uppdaterad så att det inte blir missvisande. Tack för att du kommenterade och fortsatt lycka till med plugget! /Simon
Endast Premium-användare kan kommentera.