Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1b
/ Förberedande Aritmetik
Multiplicera bråk
Innehåll
När du multiplicerar bråk så multiplicerar du täljarna med varandra och sätter resultatet i täljaren. Du multiplicerar även nämnarna med varandra och sätter resultatet i nämnaren.
Kalkylator – Multiplicera bråk
Regel för att multiplicera bråk
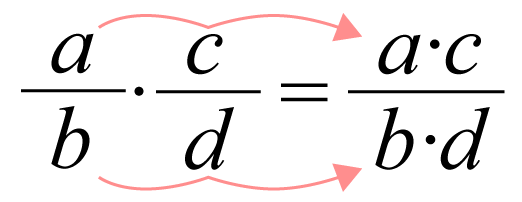
Vi multiplikation med bråk multipliceras täljarna med varandra och resultatet (produkten) placeras i täljaren. Likaså multipliceras nämnarna med varandra och produkten placeras i nämnaren.
$\frac{a}{b}\cdot\frac{c}{d}=\frac{a\cdot c}{b\cdot d}$ab ·cd =a·cb·d
Du behöver inte skriva om bråken till samma nämnare innan du multiplicerar dem!
Exempel 1
Beräkna $\frac{2}{3}\cdot\frac{1}{5}$23 ·15
Lösning
Vi börjar med att skriva om bråken på gemensamt bråkstreck, som ett mellansteg innan vi utför multiplikationen.
$\frac{2}{3}\cdot\frac{1}{5}=\frac{2\cdot1}{3\cdot5}=\frac{2}{15}$23 ·15 =2·13·5 =215
Efter en del träning kan du genomföra multipliceringen direkt i huvudet. Men vi visar här för att vara extra tydliga.
Exempel 2
Beräkna $\frac{3}{7}\cdot\frac{1}{3}$37 ·13 och svara på enklaste form.
Lösning
VI skriver om bråken på gemensamt bråkstreck.
$\frac{3}{7}\cdot\frac{1}{3}=\frac{3\cdot1}{7\cdot3}$37 ·13 =3·17·3
På så vis kan vi enklare se att täljaren och nämnaren innehåller en gemensam faktor $3$3 som vi genast kan förkorta bort.
$\frac{3\cdot1}{7\cdot3}=\frac{1}{7}$3·17·3 =17
Genom att först förkorta slipper vi stegen att först multiplicera för att sedan förkorta. Men du kan även först multiplicera och sedan förkorta svaret till enklaste form.
$\frac{3\cdot1}{7\cdot3}=\frac{3}{21}=\frac{3\text{/}3}{21\text{/}3}=\frac{1}{7}$3·17·3 =321 =3/321/3 =17
Vid bråkräkning är det bra att ta till vana att alltid svara på enklaste form, alltså förkortat, även och det inte specifikt anges att du ska göra det i uppgiften.
Multiplicera bråk med heltal
När du multiplicerar ett bråktal med ett heltal använder du dig av att exempelvis $3=$3=$\frac{3}{1}$31 eller $5=$5=$\frac{5}{1}$51 . Så du skriver först om heltalet till bråkform och sedan beräknar du multiplikationen.
Exempel 3
Beräkna $4\cdot$4·$\frac{3}{5}$35 och svara i blandad form.
Lösning
Vi kan skriva $4=$4=$\frac{4}{1}$41 och sedan beräkna
$\frac{4}{1}\cdot\frac{3}{5}=\frac{12}{5}$41 ·35 =125
Dessutom kan vi svara på blandad form då
$\frac{12}{5}=$125 = $2$2 $\frac{2}{5}$25
Multiplicera på blandad form
När ett eller flera tal i multiplikationen är skrivet på blandad form så skriver vi först om bråktalen till bråkform.
Exempel 4
Beräkna $2$2 $\frac{1}{3}\cdot\frac{3}{4}$13 ·34
Lösning
Här gör vi först om bråket som står på blandad form till bråkform. Då får vi
$2$2 $\frac{1}{3}=\frac{6}{3}+\frac{1}{3}=\frac{7}{3}$13 =63 +13 =73
Nu multiplicerar vi de bägge bråken med varandra
$\frac{7}{3}\cdot\frac{3}{4}=\frac{21}{12}$73 ·34 =2112
Du kan även förenkla bråket och sedan gå över och svara på blandad form.
$\frac{21}{12}=\frac{21\text{/}3}{12\text{/}3}=\frac{7}{4}=1\frac{3}{4}$2112 =21/312/3 =74 =134
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (5)
När svaret är i bråkform är det underförstått alltid i förkortad bråkform som söks.
Om din beräkning ger svaret$\frac{3}{18}$318 så bör du förkorta det till $\frac{1}{6}$16 innan du anger ditt svar.
-
1. Premium
Beräkna $\frac{4}{9}\cdot\frac{9}{4}$49 ·94
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Multiplicera och dividera bråktalRättar... -
-
2. Premium
Beräkna $\frac{4}{9}\cdot\frac{2}{3}$49 ·23 och förkorta så långt som möjligt.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Multiplicera och dividera bråktalRättar... -
-
3. Premium
Beräkna $\frac{1}{4}\cdot\frac{1}{2}$14 ·12
Ange svaret på formen a/b
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Multiplicera och dividera bråktalRättar... -
-
4. Premium
Beräkna $\frac{5}{7}\cdot\frac{2}{5}$57 ·25 och svara i enklaste form.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Multiplicera och dividera bråktalRättar... -
5. Premium
Beräkna $\frac{2}{3}$23 $\cdot9$·9
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Multiplicera och dividera bråktalRättar...
c-uppgifter (3)
-
6. Premium
Beräkna $3$3 $\frac{1}{5}\cdot\frac{1}{5}$15 ·15
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
7. Premium
Beräkna $3\frac{5}{6}\cdot2\frac{3}{5}$356 ·235
Svara på bråkform a/b
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: multiplicera bråk multiplikation bråkRättar... -
-
8. Premium
Beräkna $4\cdot1\frac{1}{2}\cdot0,8$4·112 ·0,8
Svara på bråkform a/b och förkorta till enklaste form
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Förlänga och förkorta bråkLiknande uppgifter: multiplicera bråk multiplikation bråkRättar... -
Olivia Lagerkvist
Gällande fråga ett. Jag skrev 1/1 som svar men det var inkorrekt, medan det korrekta svaret var 1. Är inte 1/1 = 1? I så fall bör 1/1 också vara ett korrekt svar.
Anna Eddler Redaktör (Moderator)
Hej Olivia,
det stämmer att 1/1=1.
Men då du alltid ska förkorta/förenkla så långt som möjligt när du anger ditt svar så bör du svarar 1 om det inte står att du ska svara i bråkform.
Johan Jaudat
Hej!
Jag förstår inte riktigt hur förklaringen på fråga 8? Hur får jag 1 1/2 till 3/2? och hur 0,8 blir 4/5?
Anna Eddler Redaktör (Moderator)
Hej Johan,
$1 \frac12$ är detsamma som ”en och en halv” vilket vi kan skriva som $1+\frac{1}{2}$. Genom att förlänga till samma nämnare, $2$, får vi $\frac22 +\frac12=\frac{3}{2}$ eftersom att $1$ är lika med $\frac22=\frac33=\frac{78}{78}$ osv.
Och $0,8$ är detsamma som $\frac{8}{10}$ vilket vi kan förkorta till $\frac{4}{5}$. Gick det att hänga med på?
Återvänd till lektionen om Förlänga och Förkorta av bråk om du är fortsatt osäker.
Sofia Gahm
Fel svar, det blir 0,12. Facit säger att det är addition men det är multiplikation. (1/5)*(1/5)*(3/1)=0,12
Anna Eddler Redaktör (Moderator)
Hej Sofia,
observera att första termen står i blandad form, inte som en multiplikation. Kolla förklaringen på uppgiften för att få förtydligat vad jag menar!
Tom Carlsen
stämmer fråga 6?
David Admin (Moderator)
Ja.
Första termen står i blandad form och motsvarar tre hela och en femtedel vilket är det samma som sexton femtondelar. Hör gärna av dig igen om det känns fortsatt konstigt.
Endast Premium-användare kan kommentera.