Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Vad är en funktion
En funktion beskriver alltid ett samband mellan två eller flera olika saker. Det samband som finns kan alltid beskrivas med en regel/formel. Vanligt är att man använder variabeln xx och variabeln yy för att beskriva detta samband.
I den här lektionen går vi igenom grunden i funktionsläran. Vad är en funktion? Hur beskrivs funktionen med en formel? Hur kan vi bestämma olika xx– och yy-värden för och med en funktion? Vi tar det från början.
Tre olika sätt att beskriva funktionen
I denna kurs kommer vi jobba med tre olika sätt att beskriva samma samband. Vi kommer beskriva funktionen med en ekvation eller formel, med en värdetabell och med en graf.
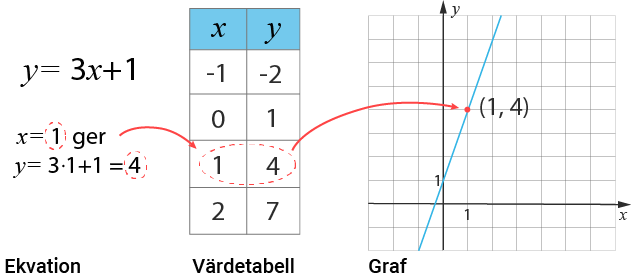
Vi ska öva på att kunna röra oss fritt mellan dessa tre olika beskrivningar av funktionens samband.
I korthet gäller följande. Ekvationen som beskriver funktionssambandet innehåller två obekanta. Ofta ett xx och ett yy. Genom att sätta in olika xx -värden i ekvationen kan du beräkna de tillhörande funktionsvärdena. Dessa talpar, xx och yy, kan du föra in i en värdetabell. Talparen motsvarar koordinater till olika punkter på grafen.
Viktigt att lägga på minnet är att värdena i tabellen motsvarar punkter på grafen. Och alla punkternas koordinater uppfyller likheten i funktionens ekvation.
Funktion – Ett samband mellan oberoende och beroende variabler
Låt säga att vi har ett samband mellan x och y, där y alltid är dubbelt så stort som x. Det här sambandet kan matematiskt beskrivas med formeln y=2x.
Detta samband kallas för en funktion och är ett samband mellan ett invärde och utvärde. För varje xx-värde vi stoppar in i formeln y=2xy=2x, kommer vi få ut ett dubbelt så stort yy -värde.
Variabeln som stoppas in i funktionen kallas för en oberoende variabel och motsvaras ofta i funktionssammanhang av ett xx -värde.
Utvärdet som ges av funktionsuttrycket kallas för en beroende variabel och betecknas ofta med ett y.
Vi skulle kunna se sambandet, eller formeln, som beskriver sambandet som en slags ”funktionsmaskin”.
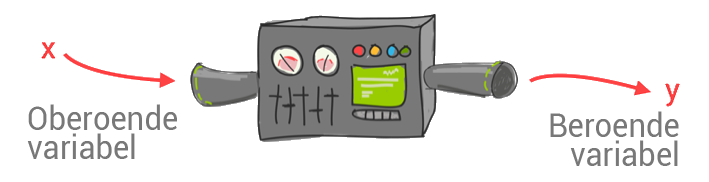
Det vi stoppar in i funktionen, i vår så kallade funktionsmaskin, är alltså det oberoende värdet, ofta xx. Sedan händer det något med värdet inne i formeln, eller funktionsmaskinen, och ut kommer ett y-värde.
yy -värdet som kommer ut är alltså beroende av vilket xx -värde som stoppas in och vad som händer med xx -värdet i funktionen.
Beteckningen f(x)
Man brukar använda beteckningen f(x) för funktioner, det utläses som ”f av x”, för att beskriva den formel som anger vad som händer i funktionen.
Viktigt att lägga på minnet att allt som oftast är y=f(x).
Exempel 1
Bestäm f(2) då f(x)=4x+1
Lösning
Vi beräknar f(2), vilket utläses som ”f av två”, genom att byta ut alla xx -värden i formeln f(x)=4x+1 mot en tvåa.
Vi får att då x=2x=2 är
f(2)=4⋅2+1=8+1=9
Funktionen f(x)ƒ (x) värde då x=2x=2 är enligt våra beräkningar lika med nio. Vi skriver det som f(2)=9ƒ (2)=9.
Genom att stoppa in olika xx -värden beräknar vi funktionens olika yy -värden.
Exempel 2
Bestäm det tillhörande yy-värdet då y=f(x) och f(x)=3x+2.
a) x=1
b) x=0
c) x=(−1)
Lösning
a) Om x=1 så är f(1)=3⋅1+2=3+2=5, Dvs y=5.
b) Om x=0 så är f(0)=2⋅0+2=0+2=2, Dvs y=2.
c) Om x=−1 så är f(−1)=3⋅(−1)+2=−3+2=−1, Dvs y=−1.
Dessa xx– och yy -värden bildar tillsammans koordinaterna till olika punkter.
x=1 och y=5 bildar punkten (1, 5)(1, 5)
x=0 och y=2 bildar punkten (0, 2)(0, 2)
x=−1 och y=−1 bildar punkten (−1,−1)(−1,−1)
Dessa punkter kan man plotta ut i ett koordinatsystem och sammanbinda för att få en grafisk avbildning av funktionen eller sammanställa i en värdetabell.
Värdetabell
Genom att välja värden på xx och beräkna det tillhörande yy -värdet kan du få koordinater som du kan sammanställa i en värdetabell. Ovan beräknade vi funktionsvärden för x=−1x=−1, x=0 x=0 och x=1x=1 funktionen f(x)=3x+2. Lägger vi även till att då x=2x=2 är y(2)=3⋅2+2=8y(2)=3·2+2=8 får vi värdetabellen nedan.
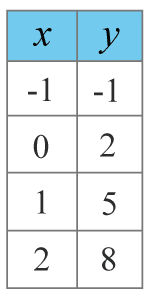
Du kan välja vilka xx -värden du vill i värdetabellen så länge de tillhör definitionsmängden. Men ett tips är att i alla fall beräkna funktionsvärdet för x=0x=0. När vi jobbar med linjära funktioner kommer nämligen grafen alltid skära yy-axeln i den punkten och avslöja en del av funktionens ekvation. Men mer om det i kommande lektioner.
Som vi nämnde tidigare gäller att värdena i tabellen motsvarar punkter på grafen. Och alla punkterna uppfyller likheten i funktionens ekvation.
Grafen
Punkterna i värdetabellen kan du plotta in i ett koordinatsystem och sammanbinda med en linje. På detta sätt har du konstruerat funktionens graf.
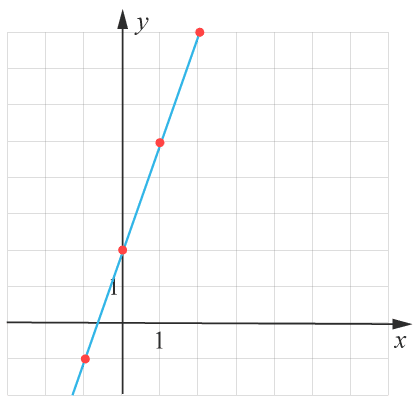
I denna kurs kommer vi jobba mycket med de linjära funktionerna. Deras graf är alltid en rak linje. Men det finns många andra funktioner och grafer med. Men mer om de senare.
Genom att läsa av punkter i grafen kan du skapa en värdetabell och bestämma grafens ekvation.
I kommande lektioner går vi igenom mer ingående de olika beskrivningarna ekvation, värdetabell och graf och hur man kan läsa av informationen mellan dessa olika samband.
Graf och funktion
Vi kommer till största del att behandla grafer som motsvarar en så kallad funktion. Alla funktioner kan illustreras med en graf, men alla grafer illustrerar inte funktioner. För en funktion gäller nämligen följande.
En funktion är en regel som till varje tillåtet xx-värde ger exakt ett yy -värde.
Alla tillåtna xx -värden, alltså xx -värden som gör att du kan bestämma ett funktionsvärde, kallar man för en definitionsmängd. Vilka xx-värden som är tillåtna varierar från funktion till funktion. Lär dig mer om detta i lektionen definitionsmängd och värdemängd.
Du kan undersöka om grafen illustrerar en funktion genom att du för en lodrät linje över grafen. Din lodräta linje får då endast skära grafen i en enda punkt i taget för att den ska uppfylla kriteriet för en funktion. Detta test kallas för vertikaltestet.
Vertikaltest
Exempel 3
Ange vilken eller vilka av graferna som är funktioner.
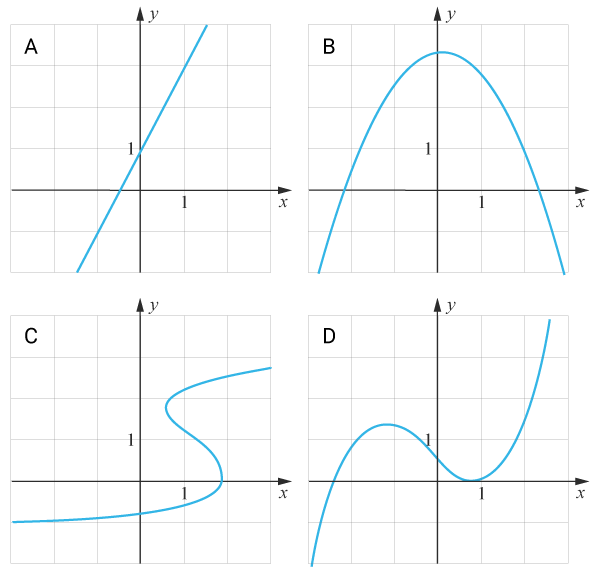
Lösning
Grafen är en funktion om varje tillåtet xx-värde ger exakt ett yy -värde. Med vertikaltestet kan vi kontrollera graferna.
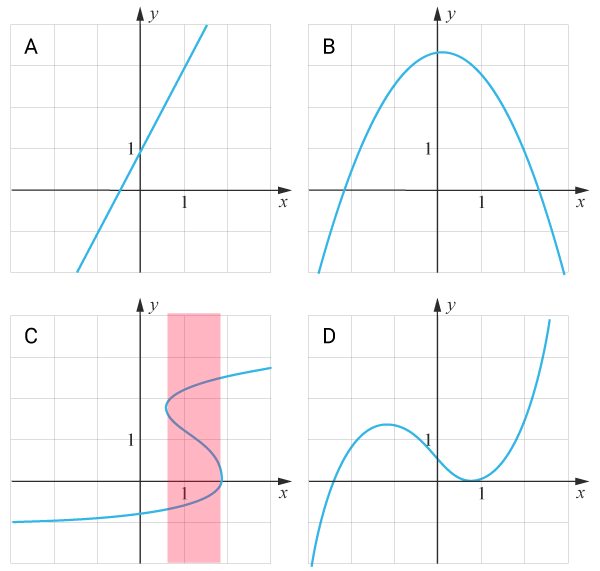
Vi låter en lodrät linjen förflytta sig över graferna och upptäcker att den skär i endast en punkt i tager på graferna A, B och D. Dessa är alltså funktioner. Men för de xx -värden som är markerade i ett rött intervall i graf C gäller att en lodrät linje skär grafen i fler än en punkt samtidigt vilket innebär att att den inte är en funktion.
Exempel i videon
- f(x)=3x+1, beräkna f(1) och f(3).
- Beskriv funktionen f(x)=2x+1 med hjälp av en värdetabell och rita ut funktionen i ett koordinatsystem.
Kommentarer
e-uppgifter (19)
1.
(1/0/0)E C A B 1 P PL M R K Nedan illustreras grafen för funktionen y=f(x)y=ƒ (x). Bestäm funktionsvärdet f(2)ƒ (2)
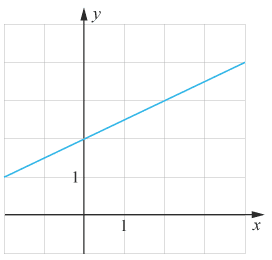 Svar:Ditt svar:Rätt svar: f(2)=3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: f(2)=3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B 1 P PL M R K Beteckningen f(x)ƒ (x) är vanligtvis det samma som…
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K Figuren visar ekvationen, värdetabellen och grafen till y=f(x)y=ƒ (x).
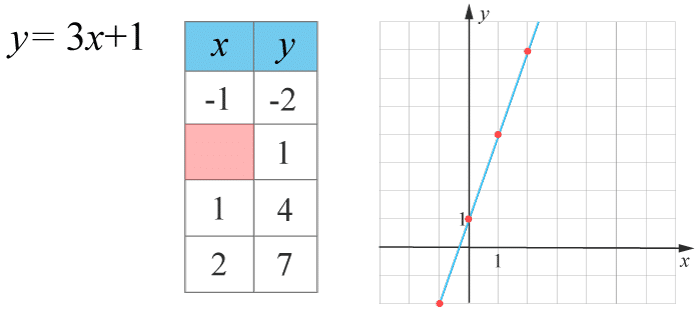
Ange det värde som saknas i den röda rutan.
Svar:Ditt svar:Rätt svar: 0(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K Figuren visar ekvationen, värdetabellen och grafen till y=f(x)y=ƒ (x).
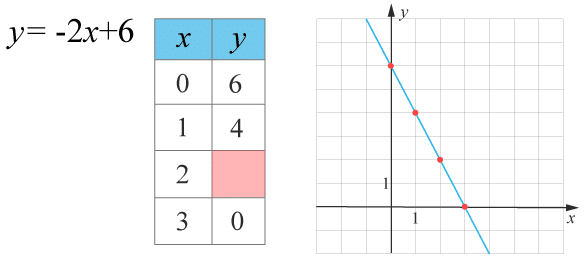
Ange det värde som saknas i den röda rutan.
Svar:Ditt svar:Rätt svar: 2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B 1 P PL M R K Ange den värdetabell som tillhör funktionen y=3x−1y=3x−1
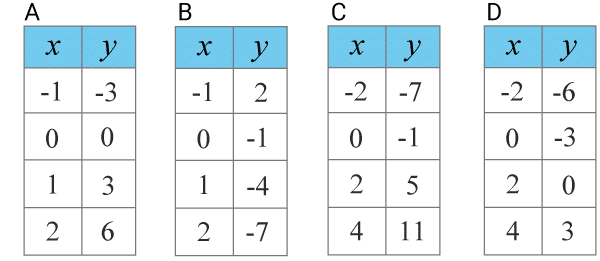 Svar:Ditt svar:Rätt svar: Värdetabell C(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: Värdetabell C(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B 1 P PL M R K I koordinatsystemet är grafen till y=4x−1y=4x−1 utritad.
Dra punkten utmed grafen dit funktionsvärdet är −5−5 .0,0Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(1/0/0)E C A B 1 P PL M R K Då ett funktionsuttryck skrivs på formen y=f(x)y=ƒ (x) kallas variabeln xx för den…
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(1/0/0)E C A B 1 P PL M R K Då ett funktionsuttryck skrivs på formen y=f(x)y=ƒ (x) kallas variabeln yy för den…
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...9. Premium
(1/0/0)E C A B 1 P PL M R K Beräkna f(1)ƒ (1) om f(x)=4x−2ƒ (x)=4x−2
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(1/0/0)E C A B 1 P PL M R K Ange det värde på mm som ger att värdetabellen tillhör funktionen y=2x−2y=2x−2
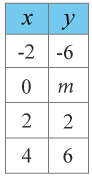 Svar:Ditt svar:Rätt svar: m=−2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: m=−2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...11. Premium
(1/0/0)E C A B P 1 PL M R K Beräkna f(−2)ƒ (−2) om f(x)=x2+1ƒ (x)=x2+1
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...12. Premium
(1/0/0)E C A B 1 P PL M R K Bestäm f(−1)ƒ (−1) då f(x)=−3x2−x+5ƒ (x)=−3x2−x+5
Svar:Ditt svar:Rätt svar: f(−1)=3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...13. Premium
(1/0/0)E C A B 1 P PL M R K Grafen visar funktionen y=f(x)y=ƒ (x). Bestäm funktionsvärdet f(5)ƒ (5)
 Svar:Ditt svar:Rätt svar: f(5)=1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: f(5)=1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...14. Premium
(1/0/0)E C A B 1 P PL M R K Grafen visar hur mycket det kostar att anlita en målare.
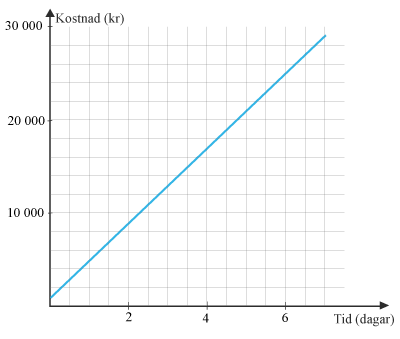
Hur mycket kostar det om målaren gör ett jobb hemma hos dig måndag till och med torsdag under en vecka?Svar:Ditt svar:Rätt svar: 17 000 kr(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...15. Premium
(1/0/0)E C A B P PL M R 1 K För vilket xx gäller att f(x)=−2x+2ƒ (x)=−2x+2 har funktionsvärdet noll?
Svar:Ditt svar:Rätt svar: x=1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...16. Premium
(1/0/0)E C A B 1 P PL M R K Vilken funktion kommer alltid ge dig ett udda tal oavsett vilket heltalsvärde du väljer på xx ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...17. Premium
(1/0/0)E C A B 1 P PL M R K Dra den röda punkten till en punkt (x, y)(x, y) på grafen där x>0x>0 och f(x)=4ƒ (x)=4
0,0Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...18. Premium
(1/0/0)E C A B 1 P PL M R K Ett badkar rymmer 150150 liter vatten. Grafen nedan visar hur lång tid det tar att tömma badkaret.
Hur lång tid tar det att tömma hela badkaret?
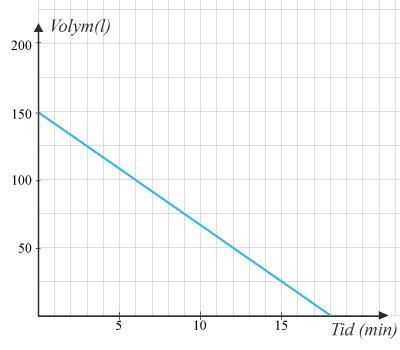 Svar:Ditt svar:Rätt svar: 18 minuter(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 18 minuter(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...19. Premium
(1/0/0)E C A B 1 P PL M R K Ett badkar rymmer 150150 liter vatten. Grafen nedan visar hur lång tid det tar att tömma badkaret.
Hur lång tid tar det att tömma badkaret till hälften? Svar:Ditt svar:Rätt svar: 9 minuter(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 9 minuter(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Magnus Hagbard
Hur får ni (−2)² + 1 till 5? -2² blir väl -4? sedan adderar man 1 = -3? Alla räknare jag testar på säger -3 men jag får fel på det. Fråga 11.
Anna Eddler Redaktör (Moderator)
Hej Magnus,
När det står en parentes runt (−2) ska det negativa talet två kvadreras. Alltså (−2)2=(−2)⋅(−2)=4 eftersom att två negativa tal gånger varandra ger en positiv produkt.
Hade det stått −22 så är det en positiv två som ska kvadreras och sedan ges en negation. Alltså $-2^2=-(2\cod2)=-(4)=-4$
Hoppas det gick att se skillnaden i detta.
Tove Zetterström
Hej,
Och tack för en fantastisk sida!
Fråga 14 är formulerad så att en målare kommer måndag till torsdag, vilken enligt den matematiska logiken borde ge tre dagar: måndag, tisdag och onsdag.
Annars borde det ha hetat ”måndag till och med torsdag”, eller har jag fel?
Vill inte vara en sån som märker ord i onödan, men har fått för mig sånt är av vikt i matematiken.
Anna Admin (Moderator)
Tack, Tove, för ditt påpekande.
Jag korrigerar till ditt önskemål.
Lycka till med matten!
Judith Lysell
Hej!
På fråga 10 fick jag fel för svaret ”9 min”. 🙂 Kanske ett svar att lägga till?
Tack för en toppensida!
David Admin (Moderator)
Fixat!
Emma Larsen
Vissa svar får man fel på bara för att man inte skriver exakt som det är bestämt. Ex: får fel om jag skriver x=1 istället för bara 1 och ibland får jag rätt på det… Samma var med en tidigare uppgift där jag skrev ”Steg 1” men fick fel svar för att svaret skulle vara ”I steg 1”
David Admin (Moderator)
Hej.
Tack för att du hör av dig. När man löser en ekvation ska man svara med x= . Just här frågade uppgiften efter vilket ”x-värde..”, vilket gör att man skulle kunna nöja sig med att svara 1. Men jag har lagt till det svaret i denna uppgift.
Vi försöker skriva in flera olika svarsalternativ som ger rätt, men ibland så missar vi eller kommer inte på alla möjliga rätta svar. Fortsätt gärna höra av dig med fler svar du anser inge ger rätt så ska vi försöka korrigera dem snarast möjligt.
Tack för hjälpen och lycka till med matten!
Sebastian Berntsson
uppgift 2-3, går inte att dra punkten???!!
Anna Admin (Moderator)
Hej Sebastian.
Vilken webbläsare använder du? Jag rekommenderar dig att prova i Chrome. Jag provade nyss och det var inget problem där.
Lycka till.
Keli Liljedahl
Hej,
På fråga 1 borde inte svaret svaret vara att x är -1 istället för 1?
Känner mig inte klokare på förklaringen med ekvationen.
Mvh Keli
Keli Liljedahl
dvs jag förstår inte hur du löser ekvationen:
-2x+2=0
2x=2 (hur får du fram detta? )Det är här jag inte hänger med.
Simon Rybrand (Moderator)
-2x+2=0
Addera med 2x
2=2x
Kan även skrivas som
2x=2
x=1
Simon Rybrand (Moderator)
Tänk på att det är ett minustecken där framför tvåan.
marcus friede
f(x)=3x+1
Kan ”3” vara vilket tal som helst?
varför är det +1 i slutet? vad anger det?
Simon Rybrand (Moderator)
Hej
Ja talet framför x kan egentligen vara vilket tal som helst. Generellt så kallas det talet för k-värde i en linjär funktion.
Nathalie Wallin
Om man har funktionen f(x)=5-3x-2x^2
och ska bestämma f(3)-f(-1)
Hur ska man göra detta?
Simon Rybrand (Moderator)
Sätt in x=3 i funktion och räkna ut värdet och gör likadant med x=−1. Beräkna sedan f(3)−f(−1). Du får då
f(3)−f(−1)=(5−9−18)−(5+3−2)=−28
Konrad Milton
Hej!
Kanske något som man borde veta men varifrån kommer talet 3 och + 1 ifrån i era exempel?
f(3) = 3*3+1 y=10
f(1) = 3*1+1 y=4
3 multipliceras med X värdet och sedan adderas 1, är det en regel som gäller för alla funktioner?
Tacksam för svar
Simon Rybrand (Moderator)
Hej
Det beror på vad vi skall sätta in i funktionen och sätter vi in talet 3 så byts x ut mot det talet i funktionsformeln.
Hanna Moraddana
Hej,
Jag tycker att Er videoklipp är oerhört bra. Man förstår grunderna väldigt bra eftersom det går till på ett mycket tydligt sätt fram.
Tack!
Lena Flodqvist
Hej!
Fantastiskt sätt att få förklaringar i videorna, tack.
Funderar på hur y i videon kunde bli oberoende om x=3 och y=10, var det inte bara x som var oberoende?
Mvh Lena
Simon Rybrand (Moderator)
Hej Lena
Det skall förstås inte stå/sägas den oberoende variabeln y utan den beroende. Vi fixar detta omgående!
Karl
Hej! Jag undrar vad som menas med ”låt”?
Låt f(x)=2x+4 och g(x)=1−3x, förenkla f(g(x)).
Vad är det man vill säga med ”låt”?
Simon Rybrand (Moderator)
Hej
Andra sätt att uttrycka samma sak på kan vara
”funktionen f(x)=2x+4” eller ”Sätt f(x)=2x+4”.
Det är alltså ”matematiska” för att låta en funktion vara lika med ett uttryck.
Arsema Kifle
Hej, kan du vara snall och forklara uppgift 2 mer utforligt?
tack pa forhand!
Simon Rybrand (Moderator)
Har lagt till en extra förklaring på den uppgiften.
Alexander Fredriksson
Hej!
Jag fattar inte hur detta funkar (alltså fråga 7 på testet):
f(2a)=3⋅(2a)2+4⋅(2a)=12a2+8a
Jag får det till 6a^2+8a.
Ska man först höja upp 2^2 så att det blir 4 å seda ta det gånger 3 å på så vis få 12?
Simon Rybrand (Moderator)
Hej
I (2a)2 så upphöjer du både 2 och a med 2 så att du får
(2a)2=22a2=4a2
Sedan multiplicerar du med 3. Den potensregel som används där är
(ab)c=acbc
Judith Sandström
Hej i uppgift 6 på avsnittet ”Vad är funktioner?” så är det ett teckenfel, svaret 2x-1 men i förklaringen står det 2x+1
Hälsningar Judith
Simon Rybrand (Moderator)
Tack för att du sade till! Har fixat det.
vanessa tv
Hej!
Om det står så här i en uppgift:
Rita graferna till följande funktioner:
A) y=2x b) y=-2x c) y=2
Ska jag då själv bestämma vad x ska vara och finns det några regler för vilka siffror det ska vara i så fall?
Simon Rybrand (Moderator)
Hej
Alla dessa tre funktioner är räta linjer och när man skall rita ut sådana så räcker det faktiskt med att välja två x-värden för att kunna rita ut linjen. Så du kan helt enkelt välja exempelvis x=1 och x=3 och räkna ut y-värdet. Sedan har du två punkter i koordinatsystemet och du kan binda samman dessa punkter med en linje. Hade du valt två helt andra x-värden hade du fått två andra punkter men de hade ändå legat på samma linje.
Annastina Ek
Hej!! Jag har kollat igenom era videor och gillar dom skarp.
Men nu är det så jag har fastnat på ett tal som jag skulle vilja ha en förklaring till och hjälp med.
Genom vilken punkt på y-axeln passerar grafen till den linjära funktionen.
y= 2 + 5x
Simon Rybrand (Moderator)
Hej
När grafen skär y – axeln så gäller att x alltid är lika med 0. Så då kan vi sätta in x = 0 i funktionen och får då
y=2+5∗0=2
Kika gärna på räta linjens ekvation, där går vi igenom det som kallas för m värde och är samma sak som y värdet där linjen skär y-axeln.
Astridmjornebrant
Hej!
Rätt svar på fråga 6 ser inte likadan ut som beskrivningen för att det är rätt.
I talet är det rätta svaret f(x)=2x-1 medan du i din beskrivning har talet f(x)=2x+1.
Båda kommer visserligen vara udda, men jag blev lite snurrig när de hade olika tecken.
Lisa
Hej! Jag förstår inte hur jag räknar ut uppgift 7. Vill du möjligtvis förklara samt hänvisa till vad jag behöver plugga på för att förstå sådana mattetal? Antar att det är någon regel jag inte minns..
Mvh Lisa
Simon Rybrand (Moderator)
Hej Lisa,
Jag tror att en viktig sak att kika lite extra på kring de talen är de så kallade potensreglerna och i det här fallet potensregeln
(ab)c=acbc.
Sedan tror jag även att det är viktigt att förstå begreppet f(x) och hur du kan sätta in olika x – värden i funktionen.
I det här fallet är det ju även så att vi inte sätter in ett tal som x – värde utan 2a så det kan ju också ställa till det lite. Principen för hur det görs är dock densamma men du behöver som nämns här ovan räkna med algebraiska uttryck och använda dig av potensregler för att kunna förenkla uttrycket.
Skarpan
Hej, har svårt att förstå tankegången när man i tal 7 och 8 linjära funktioner matte 2 b skall förenkla och sätta in g och a. Var kan jag hitta mer förklaring kring lösningen.
Simon Rybrand (Moderator)
Hej
Där gör man så att man istället för att sätta in ett tal i funktionen så sätts ett annat algebraiskt uttryck in istället för x. Detta kan vara lite ovant i början men det fungerar precis på samma vis som när du sätter in ett tal (dvs byt ut x mot ett algebraiskt uttryck).
Så om vi har funktionen f(x)=3x2+4x och beräknar några olika varianter så kan vi tex få
f(2)=3⋅22+4⋅2=12+8=20
f(2a)=3⋅(2a)2+4⋅(2a)=12a2+8a
f(2x+1)=3⋅(2x+1)2+4⋅(2x+1) =3⋅(4x2+4x+1)+8x+4
=12x2+12x+3+8x+4 =12x2+20x+7
I alla exempel här ovan använder vi samma funktion och byter ut x mot antingen ett tal eller ett algebraiskt uttryck. Hoppas att den här förklaringen hjälper dig vidare!
GabriellaR
Hej! I uppgift 7, hur kan det blir 12a^2?
Tack!
Simon Rybrand (Moderator)
Hej, det beror på att du där får
3⋅(2a)2=3⋅(22a2)=3⋅(4a2)=3⋅4⋅a2=12a2
Kika gärna på potensreglerna där vi bland annat går igenom potensregeln (ab)c=acbc som används här.
Ditte Jardmark
Hej! i fråga 8 ska man sätta in g i x varför inte tvärtom? förstår inte principen bakom
Simon Rybrand (Moderator)
Ja där skall vi sätta in g(x) i funktionen f(x), dvs vi skall förenkla
f(g(x)). Det kan ju vara lite nytt att vi sätter in en annan funktion istället för ett tal men principen fungerar på samma vis.
Så om vi har f(x)=2x+4 och beräknar f(2) får vi
f(2)=2⋅2+4=8
Här byter vi alltså ut x mot talet 2. Om vi sätter in g(x) så byter vi istället ut x mot funktionen (1-3x). Då får vi istället
f(g(x))=f(1−3x)=2⋅(1−3x)+4=2−6x+4=6−6x
abdi
Fråga 8.
Jag förstår inte hur det blev 2(1-3x) + 4. Det står ju g(x) = 3X. vart fick du 1 ifrån?.
Simon Rybrand (Moderator)
Hej
Det verkar ha blivit fel vid inmatningen av den uppgiften, det är korrigerat.
Ebba Andhult
hej, när jag skulle göra uppgift två försvann punkten och jag kunde inte sätta ut den igen, hur gör jag om detta skulle hända igen?
Simon Rybrand (Moderator)
Hej
Det skall inte behöva bli så, vi skall kolla på vad som tekniskt går fel där. Du skall alltså inte behöva göra något speciellt med detta utan vi får felsöka vart problemet ligger.
Simone Rosengren
Har ni något enkelt sätt att förklara hur man räknar ut det på enklaste sätt? i filmen väljs ju siffran helt fritt. Alltså inga uträkningar som i exemplen. tex, f(-2) om f(x) = x² +1. Hur tänker man?
Simone Rosengren
Videon ger ju ingen förklaring till hur man räknar ut räkneexemplaren, fattar verkligen ingenting när jag ska ta videoinformationen och använda den på det. Axelsystemet hjälper ju inte mig någonting när ni inte förklarat hur man faktiskt räknar ut typ – någonting
Simon Rybrand (Moderator)
Hej,
Vilken uppgift är det som du tycker är svår att lösa? Dels kan vi hjälpa dig vidare här i kommentarerna samt att vi kommer att uppdatera denna video inom kort så det är bra att veta lite mer vad du jobbar med. Det finns ju även en hel del fler videos på området funktioner som fördjupar och förklarar mer kring detta begrepp.
Emma
Hej!
Vad har dem olika bokstäverna och siffrorna för betydelse i t.ex. Formeln y=2x+3. Alltså vad har y för betydelse/ funktion och samma med 2x och 3
Simon Rybrand (Moderator)
Hej, kika lite mer på vår video om räta linjens ekvation så tror jag att delar av det kommer att förklaras!
Madelene nordkvist
Hej, är så oerhört tacksam att jag hittade denna sida
nti_ma2
Skit bra tips o videos vilket gör att man förstår lättare.
Om de står att man ska rita en graf till följande funktion: y=2
Hur f’n ska man lyckas med de??
Simon Rybrand (Moderator)
Om du skall rita grafen till y = 2 så skall du rita den linje i ett koordinatsystem där y är lika med 2. Dvs det blir en horisontell linje som går genom y = 2.
Milad
Hej!
Jag undrar hur man löser denna uppgift!
För den linjära funktionen f(x) gäller att f (x) = 2 + f (x-1) och om f (5) = 1. Bestäm f (x)
Simon Rybrand (Moderator)
Sätt den linjära funktionen till f(x) = kx + m.
Du vet att
f(x) = 2 + f(x-1) ⇔
kx + m = 2 + k(x-1) + m ⇔
kx = 2 + kx – k ⇔
k = 2
Eftersom f(5) = 1 gäller att
2⋅5 + m = 1 ⇔ m = -9
Dvs f(x) = 2x – 9
Hannabe97
Hej, jag undrar hur man ska lösa uppgiften:
Bestäm f(f(2a)) om vi vet att f(x)=2x^2? För övrigt tycker jag att hemsidan är jättebra!
Simon Rybrand (Moderator)
Hej,
Du kan börja med att beräkna f(2a)=2(2a)2=8a2
Nu skall du beräkna f(f(a)) så du sätter alltså in 8a2 i funktionsuttrycket igen och får
f(8a2)=2(8a2)2=128a4
ihelveteheller
Hej, nu fattar jag funktioner (typ). Ska göra högskoleprovet om två dagar, synd att jag inte hittade kursen tidigare. Känner ändå att jag får valuta för pengarna de timmar jag hinner öva. Skitbra. Tack för enkel och bra sajt och genomgångar! 🙂
Simon Rybrand (Moderator)
Kul att du gillar sajten!
Stort lycka till på provet!
nti_ma2
Hej!
Videon hackar och krånglar. Jag har börjat om fem gånger redan, vad ska jag göra?
Simon Rybrand (Moderator)
Hej,
Om det hackar och krånglar så kan det bero på en hel del orsaker. Läs gärna igenom våra frågor och svar om detta:
/hjalp-och-guider
Fungerar det fortfarande inte bra så kontakta oss gärna!
nti_ma2
Hej!
Tack så mycket för genomgången, lärde mig mycket ! 🙂
tahani
Hej!
Tack för era filmklip, man kan lära sig mkt faktiskt.Hur kan man se resten av videorna, för att de är låsta?????
Simon Rybrand (Moderator)
Hejsan, kul att du lär dig här!
Vi har valt att göra en hel del genomgångar gratis för att man skall kunna se och testa vårt material, resten till varje kurs ingår i den del av sajten man får betala för, du hittar mer info om det här.
Magnus
om det står ”För en linjär funktion gäller
f(-2)=4
f(2)=2
Bestäm funktionen” hur löser man det?
Simon Rybrand (Moderator)
Hejsan, med hjälp av den information du har där så har du de två punkterna på linjen, dvs
(-2, 4) och (2, 2).
Sedan kan du ta fram den linjära funktionen så att den står på formen y = kx + m där k är lutning och m är y – värdet där linjen skär y – axeln.
k=−2–24–2=−42=−0,5
m ges genom att du sätter in k – värdet samt x och y för en av punkterna i y = kx + m. Vi använder oss av punkten (2, 2) och k – värdet ovan och får
2=−0,5⋅2+m⇔
m=3
Därmed är det funktion y = -0,5x + 3
Frida
Hejhej!
Jag undrar hur man gör ifall talet ser ut såhär: f(x-3) + f(x) då f(x) = 2 – 4x
Svaret ska bli 16 – 8x men jag får inte ihop det alls..
Tack på förhand!
Simon Rybrand (Moderator)
Hej, det som brukar vara lite klurigt med sådana typer av uppgifter är just f(x-3) och hur detta beräknas. Tanken är här att du sätter in (x-3) i själva funktionen. Dvs att du byter ut x mot (x-3).
Du har alltså funktionen
f(x) = 2 – 4x och beräknar
f(x-3) = 2 – 4(x-3) = 2 – 4x + 12 = 14 – 4x
Du får då
f(x-3) + f(x) = 14 – 4x + 2 – 4x = 16 – 8x
Hoppas att detta hjälper dig på vägen!
Emma Skott
Underbara videos! 🙂
Kristoffer Jealmo
Hej!
Jag tycker att videorna är utmärkta och jag lär mig massvis.
Ett stort tack!
carla
Hej, I need help! 🙂
Jag måste bestäma två funktioner, f och g, sådana att
g( f(3) ) = 21. Jag är helt förvirrad!!
Simon Rybrand (Moderator)
Hej, ett sätt är att först bestämma dig för en möjlig funktion g(x). t.ex. g(x) = 7x.
Vi vet att 3*7 = 21 så vi behöver alltså bestämma en funktion f(x) sådan att f(3) = 3. Detta gäller för f(x) = x.
Jonatan
Beskriv den linjära funktionen f(x)=kx+m om följande vilkor gäller : f(-1)=5 och f(4)=-1. Hur gör man?
Simon Rybrand (Moderator)
Hej Jonatan, här är det viktigt att förstå att f(x) = y, dvs när du sätter in ett x – värde i funktionen så blir resultatet y värdet. Av f(-1)=5 och f(4)=-1 kan du därför konstatera att du har de två punkterna:
(-1, 5)
(4, -1)
Nu kan du beräkna lutningen k i f(x)=kx+m genom att beräkna
−1−45−(−1)=−56=−1,2
Då saknar vi bara m – värdet för den linjära funktionen och det kan du ta reda på genom att sätt in k – värdet och koordinaterna för en av punkterna i formeln, dvs:
5 = (-1,2)⋅(-1) + m
m = 3,8
f(x) = -1,2x + 3,8
Alwisw
Hej!
Visst är det så att man redan av ursprunglig formel kan se lutning på linje och var den skär y-axeln? Så att den skär linjen i y i -5 och att lutningen är 3, och då kan man ju kontrollera med andra värden såsom i videogenomgången att det är rätt?
Simon Rybrand (Moderator)
Ja det stämmer att du utifrån t.ex. formeln
y = 3x – 5
vet att lutningen är 3 och att linjen skär y – axeln i y = – 5.
Då kan du t.ex. kontrollera att likheten stämmer för att undersöka om en annan punkt ligger på denna linje.
komvux_boras
hej Simon
Ska börja läsa matematic 3C men känner kanske att jag måste repetera något innan jag börjar. Kan du rekommendera någon speciell väg som jag kan ta
mvh/så
Simon Rybrand (Moderator)
Jag skulle repetera grundläggande algebra med utveckling och förenkling av algebraiska uttryck samt faktorisering, ekvationer, andragradsekvationer. Sedan kan det också vara bra att repetera linjära funktioner och andragradsfunktioner.
Simon Rybrand (Moderator)
Hej!
Det enklaste är nog att helt enkelt räkna ut de bägge kvantiteterna och jämföra.
Kvantitet 1:
f(50) – f(47) = 50k + m – (47k + m) = 50k + m – 47k – m = 3k.
(m värdena tar ut varandra)
Kvantitet 2:
f(4) – f(1) = 4k + m – (k + m) = 4k + m – k – m = 3k.
Svar: C I är lika med II
Adrian
Hur kan f(-2) om f(x) = x² +1 bli 5?
När jag räknar -2^2 får jag de till -4 på miniräknaren och i slutändan får jag svaret till -3?
Var är de jag tänker fel?
Simon Rybrand (Moderator)
Hej Adrian, det som blir fel är hur du beräknar kvadraten, dvs x2. Det du slår på din räknare är följande:
−(22)=−(2⋅2)=−4
Det du skall beräkna är
(−2)2=(−2)⋅(−2)=4
Tänk på att när du multiplicerar två negativa tal med varandra så ges ett positivt svar. Det är egentligen samma sak som att multiplicera -2 med sig självt. På räknaren bör du alltså använda parantesen runt det negativa talet.
Johannes
Hur skall man göra när man skall beräkna en funktion typ: f(x) = x^2 om x = a +1 ?
Simon Rybrand (Moderator)
Hej Johannes, det du gör är ungefär samma sak som när du beräknar en ”vanlig funktion”. Fast nu sätter du in värdet (a + 1) i variabeln x i funktionen. Så om f(x) = x^2 så får du:
f(a + 1) = (a + 1)^2 = a^2 + 2a + 1
Daniel
hur blir (a+1)^2=a^2+2a+1
var får du 2a ifrån
Simon Rybrand (Moderator)
Hej, kika gärna på kvadreringsreglerna så kommer du se att det kommer därifrån.
Det går också se genom att skriva det på följande vis:
(a+1)2=(a+1)(a+1)=
a2+a+a+1=a2+2a+1
lme
Jag gillar era filmklipp, de är lagon långa med bra exempel. Ger mig en bra start för att komma igång. För att vara lite kritisk skulle jag önska att ni gjorde videos med lite mer avancerade tal för att fördjupa sig lättare. Det kanske ni redan har gjort bara det att jag inte har tillgång till dem eftersom att jag bara kollat på gratis klipp? 🙂
Simon Rybrand (Moderator)
Hej lme! Kul att du gillar våra genomgångar, kolla gärna vår facebook grupp och vår Youtubekanal där vi har en hel del gratis också. Precis som du skriver så har vi mer problemlösning om funktioner i våra konton med genomgångar av bland annat nationella prov.
Michele scavone
Absolutly!! Jag tycker att det är en kanon och ska bli populär för de inte kan så mycket om matte.
Tack för hjälp.
Endast Premium-användare kan kommentera.