
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1b
/ Centrala Begrepp Matematik 1
Formelsamling Matematik 1
Innehåll
Här samlar vi de formler och begrepp som du har tillgång till vid Nationella provet i kurserna Matematik 1a, 1b och 1c. Följ länken för att se skolverkets Formelblad Matematik 1. Det är exakt den formelsamling du får använda vid Nationella provet.
Det är bra att använda detta formelblad under kursen för att göra dig bekant med alla formler och för att veta vilka begrepp och formler du behöver lära in utantill inför NP.
För en mer utförlig sammanfattning av alla begrepp och formler i Matematik 1a, 1b och 1c så följ länken till lektionen Sammanfattning Matematik 1.
Prefix
|
Beteckning Namn Tiopotens |
T tera $10^{12}$ |
G giga $10^9$ |
M mega $10^6$ |
k kilo $10^3$ |
h hekto $10^2$ |
d deci $10^{-1}$ |
c centi $10^{-2}$ |
m milli $10^{-3}$ |
μ mikro $10^{-6}$ |
n nano $10^{-9}$ |
p piko $10^{-12}$ |
Potenser
För alla reella tal $m$m och $n$n och positiva tal $a$a och $b$b gäller att
$a^m\cdot a^n=a^{m+n}$am·an=am+n
$\frac{a^m}{a^n}$aman $=a^{m-n}$=am−n
$a^{-n}=$a−n= $\frac{1}{a^n}$1an där $a\ne0$a≠0
$(a^m)^n=a^{m\cdot n}$(am)n=am·n
$\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$(ab )n=anbn
$(a\cdot b)^n=a^n\cdot b^n$(a·b)n=an·bn
$a^{\frac{1}{n}}=\sqrt[n]{a}$a1n =n√a
$a^0=1$a0=1
Räta linjen
$ y = kx + m $ om $y=kx$y=kx är $y$y är proportionellt mot $x$x.
Exponentialfunktion
$y=C\cdot a^x$y=C·ax där $C$C och $a$a är konstanter och $a>0$a>0 och $a\ne1$a≠1
Potensfunktion
$y=C\cdot x^a$y=C·xa där $C$C och $a$a är konstanter.
Pythagoras sats
$\text{Area}$Area $=\frac{b\cdot h}{2}$=b·h2 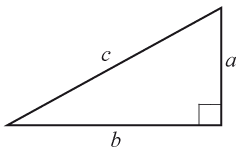
Triangel
$\text{Area}$Area $=\frac{b\cdot h}{2}$=b·h2 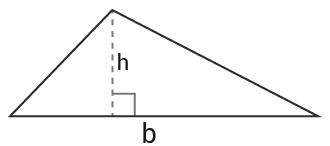
Parallellogram
$Area=b\cdot h$Area=b·h 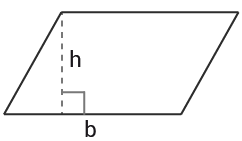
Parallelltrapets
$Area=$Area= $\frac{h\left(a+b\right)}{2}$h(a+b)2 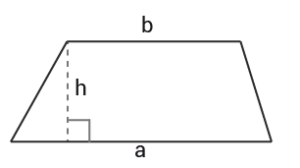
Cirkel
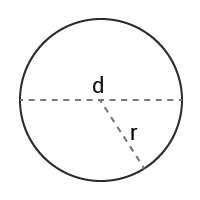
$Omkrets=\pi\cdot d=\pi\cdot2r$Omkrets=π·d=π·2r
$Area=\pi\cdot r^2=$Area=π·r2= $\frac{\pi\cdot d^2}{4}$π·d24
Cirkelsektor
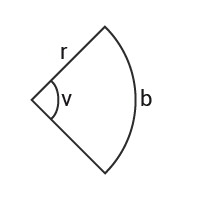
$B\text{å}gen\text{ }\text{ }b=$Bågen b= $\frac{v}{360^{\circ}}$v360∘ $\cdot2\pi r$·2πr
$Area=$Area= $\frac{v}{360^{\circ}}$v360∘ $\cdot\pi r^2$·πr2 $=\frac{br}{2}$=br2
Prisma
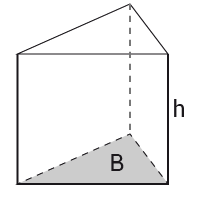
$Volym=B\cdot h$Volym=B·h där $B$B är basytans area.
Cylinder
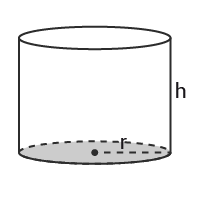
$Volym=\pi r^2h$Volym=πr2h
$Mantelarea=2\pi rh$Mantelarea=2πrh
Pyramid
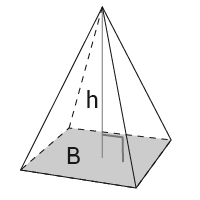
$Volym=$Volym=$\frac{Bh}{3}$Bh3
Kon
Rak cirkulär kon
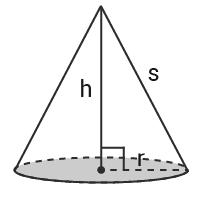
$Volym=$Volym= $\frac{\pi r^2h}{3}$πr2h3
$Mantelarea=\pi rs$Mantelarea=πrs
Klot
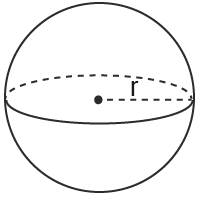
$Volym=$Volym= $\frac{4\pi r^3}{3}$4πr33
$Area=4\pi r^2$Area=4πr2
Skala
$\text{Areaskala =(Längdskala)}^2$Areaskala =(Längdskala)2
$\text{Volymskala =(Längdskala)}^3$Volymskala =(Längdskala)3
Trigonometri -Rätvinklig triangel
Definitioner
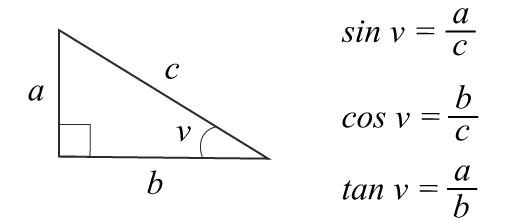

Endast Premium-användare kan kommentera.