Matematik 1b

Aritmetik
Algebra
Lån, Amorteringar och Index
Funktioner
Sannolikhetslära
Statistik
Sammanfattning begrepp och formler Matematik 1
Genomgångar nationella prov
Nationellt prov Ma1b VT 2022
Exempelprov Ma1b 2018
Nationellt prov Ma1b HT 2016
Nationellt prov Ma1b VT 2016
Nationellt prov Ma1b HT 2015
Nationellt prov Ma1b VT 2015
Nationellt prov Ma1b HT 2014
Nationellt prov Ma1b VT 2014
Nationellt prov Ma1b HT 2013
Nationellt prov Ma1b VT 2013
Nationellt prov Ma1b HT 2012
Nationellt prov Ma1b VT 2012
Breddning Ma 1b (Ingår ej i kursplanen)

Mina Kursgrupper
MV Kurser

00:00

Dela

/ Statistik

Algebra

Formler

Name: Formler - Algebra (Ma 1) - Eddler
Brand: Eddler
Rating: 3.95 (20 reviews)

Författare:Simon Rybrand

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

Innehåll

Likheter och skillnader med ekvationer och funktioner
Använda en formel
Ställa upp en egen formel
Kalkylprogram
Exempel i videon
Kommentarer

Med hjälp av en formel beskrivs ett samband med bokstäver och siffror. Formler används i områden som matematik, fysik, kemi och ekonomi. I matematiken lär du dig att hantera formler genom att kunna ställa upp dem, tolka dem och att skriva om formler.

Formel

En formel är ett samband mellan variabler och skrivs som en likhet mellan två algebraiska uttryck.

Här har vi samlat några vanliga förekommande formler in om matematiken och naturvetenskapliga ämnen.

$s=v\cdot t$ `s`=`v`·`t`	Formeln för sträcka
$R=$ `R`= $\frac{U}{I}$ `UI`	Ohms lag
$A=\pi\cdot r^2$ `A`=π·`r`²	Cirkelns area
$E=mc^2$ `E`=`mc`²	Speciella relativitetsteorin
$v=$ `v`= $\frac{s}{t}$ `st`	Formeln för hastighet
$y=kx+m$ `y`=`kx`+`m`	Räta linjens ekvation

Likheter och skillnader med ekvationer och funktioner

Begreppen ekvation, funktion och formel flyter in i varandra även om det finns tydliga skillnader. Man kan allmänt säga att en formel är ett lite bredare begrepp och att ekvationer och funktioner innehåller formler. Formeln beskriver ett samband mellan olika variabler.

En ekvation innehåller variabler som är okända där vi söker efter den okända variabelns värde, dvs lösningen på ekvationen. I en funktion beskriver istället ett samband mellan en oberoende variabel och en beroende variabel. Ofta brukar man rita ut funktioner som grafer eller beskriva dem i tabeller.

Använda en formel

När man använder sig av en formel så handlar det oftast om att byta ut formelns variabler mot ett värde. På det viset kan du ta fram värdet på en annan av formelns variabler.

Exempel 2

Formeln för att beräkna en triangels area är $A=$ A= $\frac{b\cdot h}{2}$ b·h2 . Beräkna arean om basen $b=2\text{ }cm$ b=2 cm och höjden $h=3,5\text{ }cm$ h=3,5 cm.

Lösning

För att beräkna arean så byter vi ut b mot 2 och h mot 3,5 i formeln.

$A=$ A= $\frac{b\cdot h}{2}=\frac{2\cdot3,5}{2}=$ b·h2 =2·3,52 = $3,5$ 3,5 cm $\text{ }^2$ ²

Beroende på vad vi får veta kan vi behöva flytta om i formeln, då använder vi samma principer som vid ekvationslösning så att vi får önskad variabel ensam. I exemplet ovan skulle det kunna handla om att du får veta vad arean och höjden ska vara och sedan ska beräkna basen. Nedan hittar du ett exempel vid temperaturomräkning.

Exempel 3

I USA mäter man temperaturen i Fahrenheit ( $^{\circ}F$ ^∘F) istället för i Celsius( $^{\circ}C$ ^∘C ).

För att kunna räkna om och förstå hur varmt det är när du är på besök där kan du ha god användning av följande formel $^{\circ}C=$ ^∘C= $\frac{^{\circ}F-32}{1,8}$ ^∘F−321,8 .

a) Vilken temperatur skulle vi här i Sverige säga att det är när en amerikan säger att det är $20^{\circ}F$ 20^∘F ?

b) Om det istället är $20^{\circ}C$ 20^∘C hur varmt är det i Fahrenheit?

Lösning

a) Vi ersätter $^{\circ}F$ ^∘F i formeln med $20$ 20 och får: $^{\circ}C=$ ^∘C= $\frac{20-32}{1,8}$ 20−321,8 $\approx6,7$ ≈6,7

Svar: $20^{\circ}F=-6,7^{\circ}C$ 20^∘F=−6,7^∘C,

b) Vi ersätter $^{\circ}C$ ^∘C med $20$ 20 i formeln och får: $20=$ 20= $\frac{F-32}{1,8}$ F−321,8 för att få fram graderna i Farenheit gör vi nu en ekvationslösning.

$20=$ 20= $\frac{^{\circ}F-32}{1,8}$ ^∘F−321,8 multiplicera båda leden med $1,8$ 1,8

$36=^{\circ}F-32$ 36=^∘F−32 addera båda leden med $32$ 32

$68=^{\circ}F$ 68=^∘F

Svar: $20^{\circ}C=68^{\circ}F$ 20^∘C=68^∘F

Ställa upp en egen formel

När du själv skall ställa upp en formel utifrån ett samband så kan det i början vara bra att beskriva sambandet med ord. Därefter byter du ut orden mot passande bokstäver (variabler). Om du känner att du direkt kan gå över till variabler så är det bättre att redovisa så i din lösning. Då blir redovisningen mer effektiv.

Exempel 4

Månadskostnaden för ett mobilabonnemang är 299 kr i fast kostnad och 0,5 kr per samtalsminut.

a) Ställ upp en formel för att beräkna månadskostnaden
b) Beräkna månadskostnaden om du totalt ringer 1 timme och 25 minuter den månaden.

Lösning

a) Vi kallar månadskostnaden för $K$ K. Vi kan beskriva denna kostnad på följande vis.

K = fast avgift + 0,5·(antal ringda minuter)

Vi kallar antal ringda minuter för $x$ x och får då formeln

$K=299+0,5x$ K=299+0,5x

b) 1 timme och 25 minuter är totalt $60+25=85\text{ }minuter$ 60+25=85 minuter.

Vi sätter in våra värden i formeln och får

$K=299+0,5\cdot85=341,50\text{ }kr$ K=299+0,5·85=341,50 kr

Kalkylprogram

I lektionen Beräkningar med kalkylprogram går vi igenom mer ingående hur ett kalkylprogram fungerar och hur du med det enkelt kan göra beräkningar på datamängder. Men här tittar vi kort på vilka värden olika formler i ett kalkylark ger.

=SUM summerar markerade celler
* används som multiplikationstecken. Du själv ange numeriska värden i cellen eller använda värde i celler genom att ange aktuella cellers namn.
– används om subtraktionstecken
/ används som divisionstecken

Vi tittar på ett exempel.

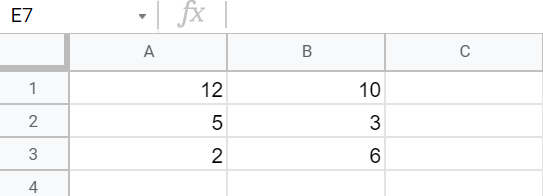
Ange värde som ges av formeln =B1*(B3-A3)

Lösning

Raderna är numrerade med en siffra och kolumnerna är namngivna med en bokstav. Man kombinerar bokstaven som anger cellens kolumn med siffran som anger cellens rad.

Genom att läsa av värdet för var cell får vi att

B1 motsvarar värdet $10$ 10

B3 motsvarar värdet $6$ 6

A3 motsvarar värdet $2$ 2

och därmed att formeln =B1*(B3-A3) motsvarar uttrycket

$10\cdot\left(6-2\right)=10\cdot4=40$ 10·(6−2)=10·4=40

Se mer ingående förklaring om kalkylblad i lektionen.

Exempel i videon

Formeln för att beräkna en cylinders volym är $V=\pi\cdot r^2\cdot h$ . Beräkna volymen om $r=3$ och $h=4$
Du jobbar som kaffeförsäljare och tjänar 500 kr per dag och har en provision på 0,5 kr per såld kaffekopp.
a) Ställ upp en formler för vad du tjänar per dag.
b) Räkna ut vad du tjänar en dag om du sålt 183 koppar kaffe.

Nästa lektion: Felkällor och felmarginal

Kommentarer

TrÃ¤na mer

E
0/10
C
0/11
A
0/6

TotalpoÃ¤ng

0/27

e-uppgifter (8)

1.
(1/0/0)
E C A

B

P 1

PL

M

R

K

Formeln för att beräkna ett fordons hastighet är $v=$ v= $\frac{s}{t}$ st

Beräkna medelhastigheten för en bil som har kört $60$ 60 km på $0,5$ 0,5 timmar.

Svara i enheten km/h.
Svar:

Ditt svar:
Rätt svar: $120\text{ km/h}$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_P Korrekt svar $120\text{ km/h}$

Rättad
Rättar...
2.
(1/0/0)
E C A

B

P 1

PL

M

R

K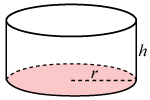

Formeln för att beräkna en cylinders volym är $V=\pi\cdot r^2\cdot h$ V=π·r²·h.

Beräkna volymen för en cylinder om $r=4\text{ }cm$ r=4 cm och $h=2\text{ }cm$ h=2 cm.

Svara med en decimals noggrannhet och enheten $\text{cm}^3$ cm³ .
Svar:

Ditt svar:
Rätt svar: $100,5\text{ }cm^3$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_P Korrekt svar. ( $100,5\text{ }cm^3$ )

Rättad
Rättar...
3.
(1/0/0)
E C A

B

P

PL

M 1

R

K

Lars säljer lotter på en marknad. Han får betala 499 kr för att få stå på marknaden och säljer varje lott för 5 kronor.

Ställ upp en formel som beskriver hans intäkter $y$ y beroende på antal lotter $x$ x han säljer på marknaden.
Svar:

Ditt svar:
Rätt svar: $y=5x-499$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_M Korrekt svar $y=5x-499$ eller $y=-499+5x$

Rättad
Rättar...

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

4. Premium
(1/0/0)
E C A

B

P 1

PL

M

R

K

Vi är vana att mäta vikt i kg men i engelskspråkiga länder används ofta pounds (lb)

Formeln för för att beräkna vikten/massan i kg om du fått den i pound är

$M_{kg}=\frac{M_{lb}}{2,2046}$ M_kg=M_lb2,2046

Hur mycket väger en låda i kg om den är märkt $150\text{lb}$ 150lb ?
Svar:

Ditt svar:
Rätt svar: $68kg$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_P Korrekt svar (68kg)

Rättad
Rättar...
5. Premium
(1/0/0)
E C A

B

P 1

PL

M

R

K

Du har en formel $u=8w-3$ u=8w−3. Beräkna $u$ u då $w=-2$ w=−2.
Svar:

Ditt svar:
Rätt svar: $u=-19$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_P Korrekt svar. ( $u=-19$ )

Rättad
Rättar...
6. Premium
(1/0/0)
E C A

B

P

PL

M 1

R

K

Kalkylbladet visar Avas inkomst under ett par veckor.

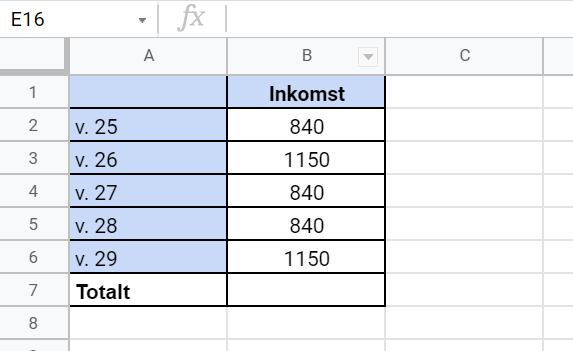
Vilket tal kommer stå i cell B7 om formeln i cellen är =B2+B3+B4+B5+B6?
Svar:

Ditt svar:
Rätt svar: $4820$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_M Korrekts var. ( $4820$ )

Rättad
Rättar...
7. Premium
(2/1/0)
E C A

B 1

P 1 1

PL

M

R

K
M

Det är mycket praktiskt att kunna räkna om mellan olika typer av längdenheter. Både på grund av att engelskspråkiga länder ofta använder inches och feet istället för cm, men även när vi i Sverige ska köpa TV eller åker till brädgården och måtten anges i tum.

$1\text{tum}=1\text{inch}=2,54\text{cm}$ 1tum=1inch=2,54cm

$1\text{fot}=1\text{feet}=30,48\text{cm}$ 1fot=1feet=30,48cm

På nätet hittar man lätt program som omvandlar åt en, datorn använder då helt enkelt denna formel för att räkna om åt dig. (d står för distance)

$d_{cm}=30,48d_{feet}+2,54d_{inch}$ d_cm=30,48d_ƒ eet+2,54d_inch

a) Du ska köpa en ny TV märkt $65”$ 65” vilket innebär att dess diagonal är $65$ 65 tum. Beräkna diagonalens längd i cm.

b) En vän till dig säger att han är ”five feet, ten(inches)” hur lång är han i cm?

c) Beräkna din egen längd i feet och inches.

Avrunda alla svar till heltal.
Svar:

Ditt svar:
Rätt svar: a)165cm b)178cm c) se förklaring...
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_B a) Korrekt svar. (165cm)
+1 e_P b) Korrekt svar. (178cm)
+1 c_P c) Se förklaring.

Rättad
Rättar...
8. Premium
(1/0/0)
E C A

B

P

PL

M 1

R

K

Max och Mia har gjort ett kalkylark över sina inkomster under v.25-29

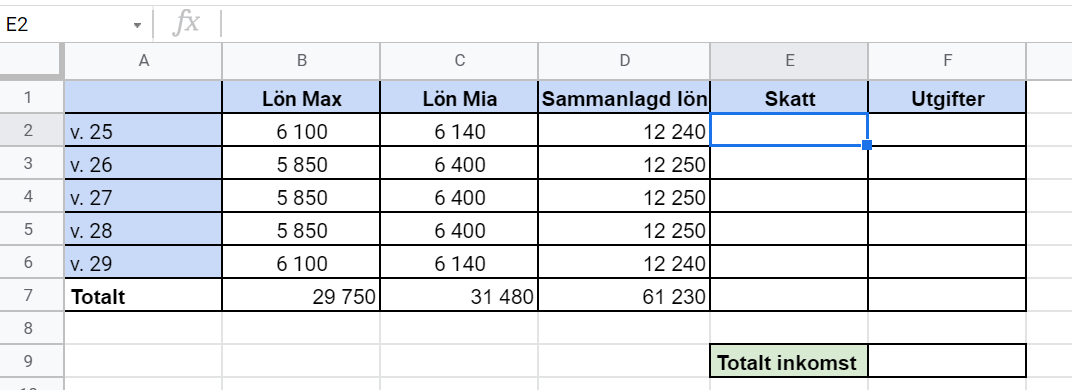
Vilket tal kommer stå i cell E2 om formeln i cellen är =0,31*D2?
Svar:

Ditt svar:
Rätt svar: $3794,40$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_M Korrekt svar. ( $3794,40$ )

Rättad
Rättar...

c-uppgifter (5)

9. Premium
(0/1/0)
E C A

B

P 1

PL

M

R

K

Formeln för att gå mellan temperaturenheterna Celsius och Fahrenheit är $^{\circ}F=1,8\text{ }^{\circ}C+32$ ^∘F=1,8 ^∘C+32.

Bestäm temperaturen i grader Celsius om temperaturen utomhus en dag är $80\text{ }^{\circ}F$ 80 ^∘F.

Svara med en decimals noggrannhet och enheten grader Celsius.
Svar:

Ditt svar:
Rätt svar: $26,7\text{ }\text{°}C$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_P Korrekt svar. ( $26,7\text{ }\text{°}C$ )

Rättad
Rättar...
10. Premium
(0/1/0)
E C A

B

P

PL

M 1

R

K

Kostnaden för elförbrukning i en bostadsrättsförening är en fast årsavgift på totalt $2400\text{ }$ 2400 kr/lägenhet samt en avgift på $0,3\text{ }$ 0,3 öre per förbrukad kWh (kilowattimme). Medlemmarna i bostadsföreningen betalar avgiften för sin elförbrukning varje månad.

Ställ upp en formel som beräknar kostnad för elen för en lägenhet per en månad. Sätt $K$ K till kostnad och $x$ x till förbrukade kWh.
Svar:

Ditt svar:
Rätt svar: $K=200+0,003x$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_M Tecknar en korrekt modell $K=200+0,003x$

Rättad
Rättar...
11. Premium
(0/2/1)
E C A

B

P

PL 1

M 1

R 1

K
M

Du har räknat ut att en gräsklippare kan klippa $0,8$ 0,8 m $^2$ ² gräs per sekund.

a) Ställ upp en formel som visar hur många $y$ y m $^2$ ² som $n$ n stycken gräsklippare klipper på $x$ x sekunder.

b) Hur många gräsklippare som det minst krävs för att klippa $1000$ 1000 m $^2$ ² på $100\text{ }$ 100 sekunder.
Svar:

Ditt svar:
Rätt svar: a) $y=n\cdot0,8x$ b) $13$ stycken gräsklippare.
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_M a)Tecknar en korrekt modell för att lösa ekvationen.
+1 c_PL b )Redovisad lösning med korrekt svar. Även utan avrundning till helt antal gräsklippare. ( $13$ st )
+1 a_R b) Eleven för ett resonemang att det inte finns halva gräsklippare

Rättad
Rättar...

12. Premium

(1/4/2)

	E	C	A
B
P	1
PL
M		2	1
R
K		2	1

M NP

I en fotoaffär trycker man rektangulära bilder på målarduk och monterar därefter bilden på en träram. Träramen kostar $0,45$ 0,45 kr/cm.
Målarduk med tryck kostar $0,12$ 0,12 kr/cm $^2$ ². Kostnad för montering är $169$ 169 kr för alla ramstorlekar.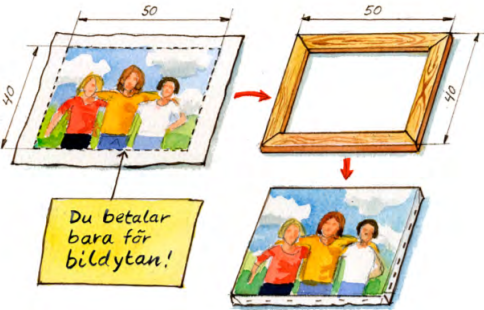

a) Yasmin vill trycka en bild och få den monterad. Hon vill ha bilden $50$ 50 cm lång och $40$ 40 cm bred.

Vad blir kostnaden?

b) För att beräkna priset på monterade bilder behöver personalen en formel där längd och bredd ingår. I priset ska ingå målarduk med tryck, ram och kostnad för montering.

Hjälp fotoaffären att göra en sådan formel.

Svar:

Ditt svar:

Rätt svar: a)

490\

kr b)

K=a\cdot b\cdot0,12+(2a+2b)\cdot0,45+169

där K = kostnaden i kr, a = längd i cm och b = bredd i cm

()

Bedömningsanvisningar/Manuell rättning

+1 e_P a) Påbörjad lösning, t.ex. beräknar kostnaden för tryck eller ram.
+1 c_K a) Redovisad lösning...
+1 c_M a) ...med korrekt svar. ( $490$ kr)
+1 c_M b) Påbörjad lösning, t.ex. ställer upp ett algebraiskt uttryck för kostnaden för tryck eller ram, med längd och bredd som variabler.
+1 c_K b) Poänget ges samtidigt som Cm
+1 a_M b) Godtagbar fullständig formel ( $K=a\cdot b\cdot0,12+(2a+2b)\cdot0,45+169$ )
+1 a_K b) med definierade variabler. (K = kostnaden i kr, a = längd i cm och b = bredd i cm)
Rättad

Se mer: Formler

13. Premium
(0/1/0)
E C A

B 1

P

PL

M

R

K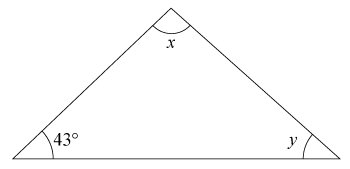
M

Skriv ett uttryck för att beräkna vinkeln $y$ y
Svar:

Ditt svar:
Rätt svar: $y=137^{\circ}-x$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_B Godtagbart svar, t.ex. $y=137^{\circ}-x$

Rättad
Se mer: Vinkelsumma i triangeln och fyrhörningen
Rättar...

a-uppgifter (3)

14. Premium
(0/1/1)
E C A

B 1

P 1

PL

M

R

K
ac NP

$15\text{ }\%$ 15 % av $a$ a är lika med $b$ b. Skriv $30\text{ }\%$ 30 % av $3a$ 3a uttryckt i $b$ b.
Svar:

Ditt svar:
Rätt svar: $6b$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_B Påbörjad lösning, t.ex. anger något samband mellan $a$ och $b$ med symboler
+1 a_P Redovisning med korrekt svar. ( $6b$ )

Rättad
Rättar...
15. Premium
(0/0/1)
E C A

B

P 1

PL

M

R

K

Stoppsträckan för en bil är beroende av bilen hastighet vid inbromsningen samt hur snabbt chauffören reagerar på att den behöver bromsa. Stoppsträckan kan beräknas med formeln

$s_t=v_0\cdot t_r+$ s_t=v_0‍·t_r+ $\frac{\left(v_0\right)^2}{2a_b}$ (v₀)²2a_b

där $s_t$ s_t är stoppsträckan, $v_0$ v₀ är bilens hastighet vid inbromsningens start, $t_r$ t_r är förarens reaktionstid, $a_b$ a_b är bilens förmåga att bromsa (retardera).

Bestäm stoppsträckan för en bil som kan bromsa in med en retardation på $2,5$ 2,5 $m$ m/ $s^2$ s² då det tar $2$ 2 sekunder för föraren att reagera och hastigheten vid inbromsningen var $35$ 35 $m$ m/ $s$ s.
Svar:

Ditt svar:
Rätt svar: $315$ meter
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 a_P Redovisad lösning med korrekt svar. ( $315$ meter)

Rättad
Rättar...
16. Premium
(0/0/1)
E C A

B 1

P

PL

M

R

K
NP

I följande uttryck är $a$ a och $b$ b längder. Vilket av nedanstående uttryck skulle kunna vara en volym?

$\frac{a}{b}$ ab $a^2b$ a²b $ab^3$ ab³ $a^2+b^2$ a²+b² $2a+2b$ 2a+2b
Svar:

Ditt svar:
Rätt svar: $a^2b$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 a_B Korrekt alternativ. ( $a^2b$ )

Rättad
Rättar...

Nästa lektion: Felkällor och felmarginal

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

Eddler

VÅR TJÄNST

POPULÄRA KURSER

FÖRETAGSINFO

Eddler AB
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg
info@eddler.se

Säker SSL-server

Vad Ã¤r detta?

HÃ¤r hittar du matematiska symboler som kan anvÃ¤ndas nÃ¤r du stÃ¤ller frÃ¥gor pÃ¥ forumet eller kommenterar. NÃ¤r du klickar pÃ¥ symbolen markeras denna, kopiera genom klicka med hÃ¶ger musknapp eller anvÃ¤nda kortkommandot Ctrl-C (PC) / cmd-C (Mac)

FÃ¶rhandsvisning Latex:

Latexkod:

Matematik 1b

Välj kurs

KURSER /

Matematik 1b

/ Statistik

Formler

Författare:Simon Rybrand

Allt du behöver för att klara av nationella provet

Allt du behöver för att klara av nationella provet

Innehåll

Formel

Exempel 2

Lösning

Exempel 3

Lösning

Exempel 4

Lösning

Lösning

Tuva Grönwall

Anna Eddler Redaktör (Moderator)

Katarina Nyström

David Admin (Moderator)

Endast Premium-användare kan kommentera.

1.

2.

3.

Allt du behöver för att klara av nationella provet

Allt du behöver för att klara av nationella provet

4. Premium

5. Premium

6. Premium

7. Premium

8. Premium

9. Premium

10. Premium

11. Premium

12. Premium

13. Premium

14. Premium

15. Premium

16. Premium

Eddler

VÅR TJÄNST

POPULÄRA KURSER

FÖRETAGSINFO

LADDAR DOKUMENT...

LADDAR GEOGEBRA...