GeoGebra och Grafisk lösning

På senare år har digitala hjälpmedel blivit en naturlig del av det vi lär oss i matematikkurserna. Det digitala verktyget GeoGebra och Grafisk lösning är ett av de moment som är ett vanligt inslag.

Självklart kan du använda en annan webbtjänst eller en grafräknare för detta, men vi tittar här på GeoGebra då det är en gratistjänst och tillgänglig för alla med uppkoppling.

Med hjälp av ett digitalt verktyg skriver vi in VL och HL som två olika funktioner och använder därefter grafräknarens verktyg för att bestämma deras skärningspunkt. 

Genom att göra följande steg kan du lösa ekvationerna grafisk.

Ekvationens lösning motsvaras av skärningspunktens $x$x-värde om det är en potens- eller exponentialfunktion. Om det är ett ekvationssystem är det både $x$x– och $y$y-värdet som motsvarar lösningen. Men det kommer först i Matematik 2.

När vi löser ekvationer är grafisk lösning en av flera lösningsmetoder. Men i Matematik 1 är den grafiska ekvationslösning det enda alternativet när vi löser just exponentialekvationer.

När du exempelvis löser exponentialekvationen $20\text{ }000=15\text{ }000\cdot1,036^x$20 000=15 000·1,036^x i Geogebra finner vi lösningen genom att skriva in VL och HL som två olika funktioner.

      1. Vi skriver in  $y=15000\cdot1.036^x$y=15000·1.036^x  som en funktion, och trycker enter.
        GeoGebra namnger ofta din funktion till något nytt då, i vårt exempel
        nedan till $f$ƒ  .

      2. På raden under skriver vi sedan  $y=20000$y=20000 och trycker enter.

Tänk på att GeoGebra använder punkt som decimaltecken. Om du skriver ett komma kommer GeoGebra i stället tolka det som en punkt $\left(x,\text{ }y\right)$(x, y) i koordinatsystemet. 

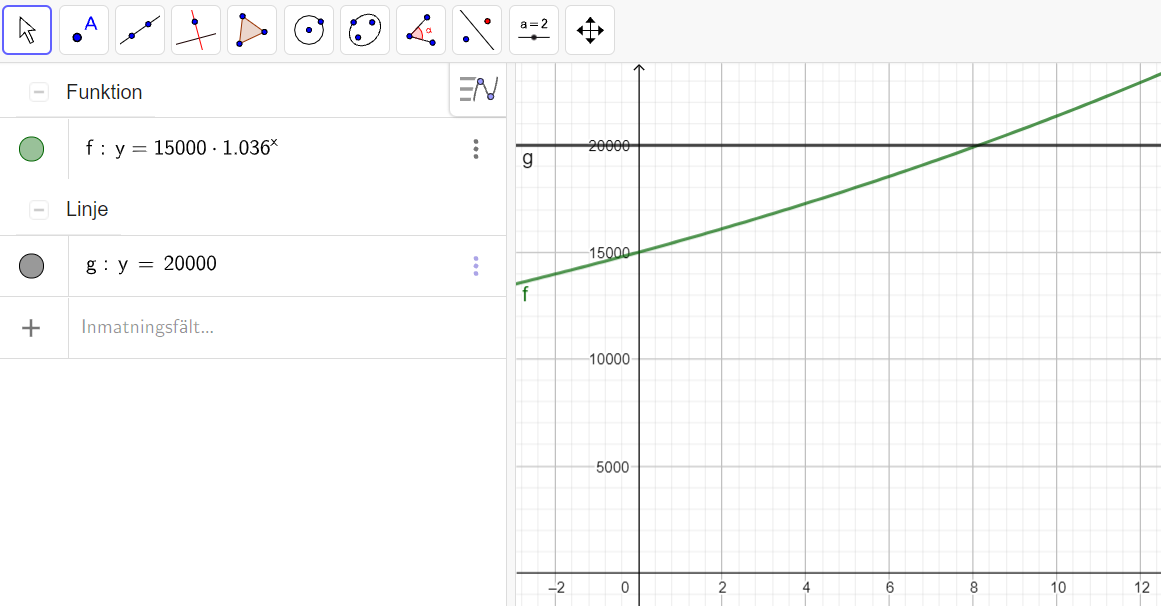
       3. Vi använder verktyget för att bestämma skärningspunkten.
           Klicka på ikonen  och välj skärningspunkt mellan två objekt.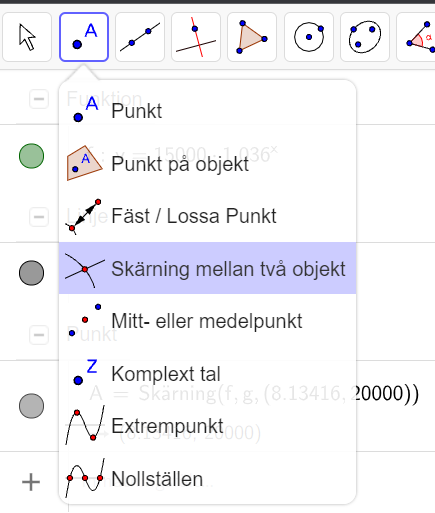

Klicka sedan på de två graferna till funktionerna och skärningspunkten $\left(8,13416;\text{ }20\text{ }000\right)$(8,13416; 20 000) anges, alternativt med färre eller fler decimaler utifrån den inställning du har i GeoGebra.

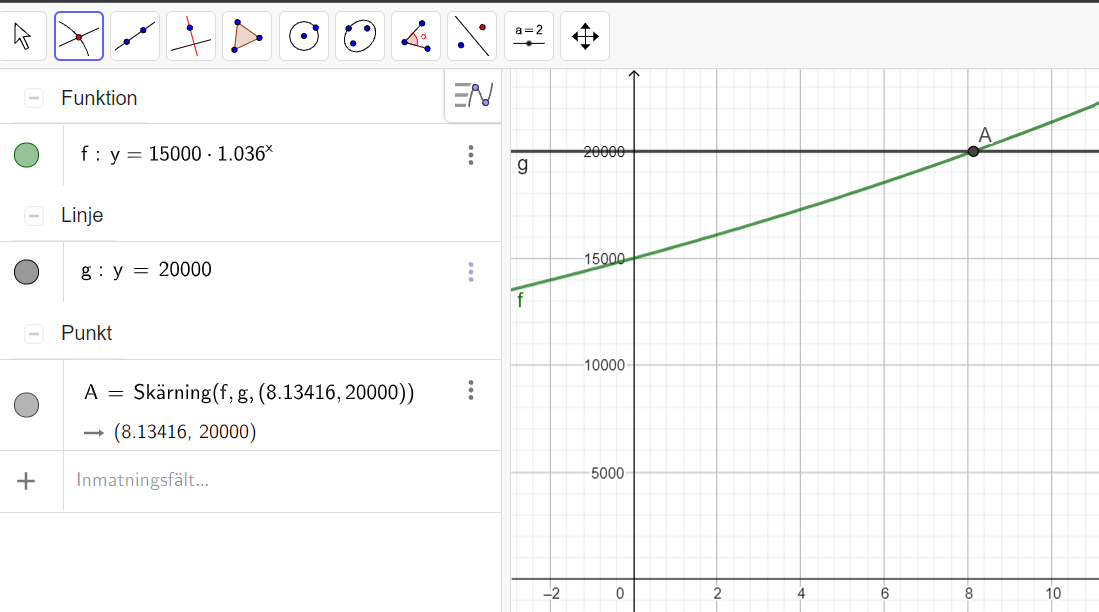
Det innebär att $y=20\text{ }000$y=20 000 när $x=8,13416$x=8,13416  vilket därmed motsvarar lösningen till ekvationen.

Ofta hittar du dessa ekvationer i en beskrivning av något vardagsexempel. En så kallad tillämpning och du behöver då tolka var ditt värde på $x$x-motsvarar.

Om det har med tid att göra så var noga med att ta reda på vad $x=0$x=0 motsvara. Är det ett särskilt årtal, datum eller ett klockslag modellen utgår ifrån? I så fall måste du ta hänsyn till det i din tolkning. Vi tittar mer på det i lektionen Exponentialfunktioner.

För att se din lösning i koordinatsystemet kan du behöver gradera om dina koordinataxlar. Ett enklat sätt att göra detta i GeoGebra är att bara klicka i ritområdet med och skrolla på musen. Då zoomar du in och ut.

Vill du bara är att bara zooma en axel i tagen kan du klicka på ikonen och sedan hålla musen över en av koordinataxlarna och skrolla. 

Bästa sättet att bli bra på detta är som med allt annat att öva! Och i matematik 2 lär vi oss om logaritmer för att lösa exponentialekvationer algebraiskt.