Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1b
/ Algebra
Linjära olikheter
Innehåll
Linjär olikhet
En linjär olikhet uttrycker en storleksrelation mellan två olika matematiska uttryck av första graden.
Man använder symbolerna $>, \, <, \, ≤, \, ≥$ för att beskriva denna relation där de betyder följande.
$x < 3$ utläses ”$x$x är mindre än tre”
$x > 3$ utläses ”$x$x är större än tre”
$x ≤ 3$ utläses ”$x$x är mindre eller lika med tre”
$x ≥ 3$ utläses ”$x$x är större eller lika med tre”
Man kallar $>$ och $ <$ för öppna olikheter, vilket innebär att variabeln inte kan anta värdet som det står i relation till.
Man kallar $≤$ och $≥$ för slutna olikheter, vilket innebär att variabeln kan anta värdet som det står i relation till.
Exempel 1
Ange vilka värden $a$a kan anta, då $a$a är ett heltal i intervallet $2<$2< $a\le5$a≤5
Lösning
Man utläser intervallet $2<$2< $a\le5$a≤5 som ” $a$a är större än två, och mindre eller lika med fem”.
$a$a kan alltså inte vara lika med två, men lika med fem eftersom att olikheten är öppen neråt med sluten uppåt. Det ger oss att $a$a kan anta heltalsvärdena $3,\text{ }4$3, 4 och $5$5
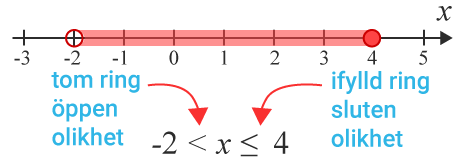
På tallinjen markeras ett öppet intervallet med en streckad, tom cirkel. De slutna intervallen markeras med en heldragen, ifylld cirkel.
Exempel 2
Ange intervallet som är markerat på tallinjen
Lösning
Ringarna markera talen $1$1 och $5$5 på tallinjen.
Ettan med en tom cirkel vilket ger en öppen olikhet.
Femman med en ifylld cirkel vilket ger en sluten olikhet.
Intervallet motsvarar olikheten $1<$1< $x\le5$x≤5.
Att lösa linjära olikheter
När man löser linjära olikheter följer man i stort sätt samma metoder som vid lösning av linjära ekvationer. Man utför samma operationer i högerledet och i vänsterledet tills att variabeln är ensam i ena ledet och lösningen är uppenbar.
Exempel 3
Lös olikheten $ x-8 > 10 – 5x $
Lösning
Vi löser en linjär olikhet på samma sätt som en ekvation.
$ x-8 > 10 – 5x $ Addera både leden med $5x$5x
$ 6x-8 > 10 $ Addera både leden med $8$8
$ 6x > 18 $ Dividera båda leden med $6$6
$ x > 3 $
Man utläser svaret som ” $x$x är större än tre”.
Olikheten byter riktning
Det finns en viktig skillnad mellan lösning av linjär olikhet och ekvationer. Undantaget är vid multiplikation och division med negativa tal. Vid dessa operationer byter olikheten riktning. Vi argumenterar för detta genom exemplet att då $3<4$3<4 måste olikheten byta riktning för att stämma vid division med det negativa talet minus ett i båda leden. Detta efter som att resultatet ger att $-3>-4$−3>−4.
Exempel 4
Lös olikheten $ -3x-8 > 10 $
Lösning
Vi löser olikheten och observerar att vid multiplikation och division med negativa tal, byter olikheten riktning.
$ -3x-8 > 10 $ Addera både leden med $8$8
$ -3x > 18 $ Dividera båda leden med $\left(-3\right)$(−3)
$ x < -6 $
Man utläser svaret som ” $x$x är mindre än minus sex”.
Kändes det här konstigt kan du kontrollera genom att lösa olikheten igen, men denna gång istället börja med att addera båda leden med $3x$3x och på så sätt få variabeln på andra sidan olikheten med med positiv koefficient.
Exempel i videon
- Beskrivning av $-2<x\le3$< span=””></x\le3$<>−2<x≤3 på tallinjen
- Beskrivning av $x<-2$x<−2 och $x\ge3$x≥3 på tallinjen
- Lös den linjära olikheten $x-5>10-4x$x−5>10−4x
- Lös den linjära olikheten $10-6x\le5-8x$10−6x≤5−8x
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (16)
-
1. Premium
Vilket alternativ stämmer in på beskrivningen
” $a$a är större än $10$10 men mindre eller lika med $100$100″.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar... -
2. Premium
Vilket av följande påståenden stämmer?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar... -
3. Premium
Vilket intervall beskriver det markerade området i figuren?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1 tallinjeRättar... -
4. Premium
Skriv en olikhet, med variabeln $x$x det intervall, som motsvarar längden på alla som är längre än $178$178 cm.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...5. Premium
Lös den linjära olikheten $x+8>10-x$x+8>10−x
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...6. Premium
Lös den linjära olikheten $2x+10\le1-x$2x+10≤1−x
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...7. Premium
Skriv en olikhet, med variabeln $x$x det intervall, som motsvarar att man INTE är myndig enligt svensk lag.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...8. Premium
Vilken olikhet beskriver bilden?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...9. Premium
Vilket värde på $x$x uppfyller inte villkoret $2x+1>5$2x+1>5?Np ht16
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Linjära olikheter nationellt prov Olikhet öppet intervallRättar...10. Premium
Vilket intervall är störst?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...11. Premium
Vilket intervall är störst?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...12. Premium
Lös olikheten $x-7$x−7 $<15$<15
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...13. Premium
Lös olikheten $3x+15$3x+15 $>3$>3
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...14. Premium
Lös olikheten $7x-10$7x−10 $>11$>11
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...15. Premium
Lös olikheten $x+2\le14-2x$x+2≤14−2x
Sluten olikhet skrivs som $x$x<= eller $x$x >=
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...16. Premium
Lös olikheten $3\left(x+2\right)\le14-x$3(x+2)≤14−x
Sluten olikhet skrivs som $x$x<= eller $x$x >=
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall Linjära olikheter modellering olikheter öppna och slutna intervallRättar...c-uppgifter (6)
-
17. Premium
Vilket eller vilka intervall är störst?
A
B
C
D
E
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...18. Premium
Ange med en olikhet alla punkter som ligger till höger om den blåmarkerade punkten.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Högskoleprovet Högskoleprovet matematik Linjära olikheter Matematik 1Rättar...19. Premium
Lös olikheten $-4x+1<$−4x+1< $3^2$32
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall linjär olikhet Olikhet olikheter öppet och slutet intervallRättar...20. Premium
Lös olikheten $2\left(3x+5\right)<$2(3x+5)< $8x+5$8x+5
Sluten olikhet skrivs som $x$x<= eller $x$x >=
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall linjär olikhet Olikhet olikheter öppet och slutet intervallRättar...21. Premium
Lös olikheten $2x+1<$2x+1< $\frac{2x+5}{3}$2x+53 $+2$+2
Sluten olikhet skrivs som $x$x<= eller $x$x >=
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall linjär olikhet Olikhet olikheter öppet och slutet intervallRättar...22. Premium
Vilket är det minsta heltal som uppfyller olikheten $2x+3>$2x+3> $x+4$x+4 ?
Träna på att motivera ditt svar.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall linjär olikhet Olikhet olikheter öppet och slutet intervallRättar...a-uppgifter (5)
-
23. Premium
Bestäm för vilka värden på $x$x som olikheten $x^2>3$x2>3 gäller.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Linjära olikheter Roten ur - AndragradsekvationerRättar...24. Premium
Vilket alternativ gäller?
Motivera ditt val i rutan nedan.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Nationellt prov Matematik 2b vt2012 DEL I och IILiknande uppgifter: nationellt prov Nationellt prov Ma1b vt12 olikheterRättar...25. Premium
Tre vänner ska jämföra värdet av två olika uttryck.
En säger att
$3n+2>2n+8$3n+2>2n+8Nästa säger att
$3n+2=2n+8$3n+2=2n+8Och den tredje menar att
$3n+2<2n+8$3n+2<2n+8Vad säger du?
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: algebraiska uttryck aritmetik Linjära olikheter olikheter resonemangRättar...26. Premium
Om $x\ge2$x≥2 och $y\ge-3$y≥−3, vilket är då det minsta värde som uttrycket $2x+y^2$2x+y2 kan anta?
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Matematik 1 nationellt prov Nationellt prov Ma1b vt12 Olikhet Prov uttryckRättar...27. Premium
För vilka värden på $y$y har olikheten $7x-y>$7x−y> $x+4$x+4 lösningen $x>1$x>1 ?
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra intervall linjär olikhet Olikhet olikheter öppet och slutet intervallRättar...Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut! -
Redigera uppgift Stäng Lägg till uppgift Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Namnet måste vara 4-60 tecken långt. Rapportera fel Lektion
{[{lessonData.title}]}
Kategori
{[{reportType}]}
ID
{[{reportId}]}
Beskriv med minst 10 tecken. Byt kurs Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Köp Premium Avbryt Din skolas prenumeration har gått ut!Övningsuppgifter ej tillgängliga!Stäng Din skolas prenumeration har gått ut!Exempel i videon. 
Logga in
viaeller medGör om alla uppgifter All svar raderas. Detta går inte att ångra detta.
Radera Avbryt Genom att använda den här sidan godkänner du våra användarvillkor, vår integritetspolicy och att vi använder cookies. -
-
Maruxs M
Hej, skulle ni kunna förklara i fråga 27?
Hur blir det 1″≥”? och inte 1″>”?
Då vi söker de värden som ger att x>1 innebär det att
” 1≥ 4+y/6″
Tacksam för svar!
Thaimi L. Bolander
Tal 22 år också fel! Det korrekta svaret X > 1 vägras accepteras som rätt lösning!
Korrigera gärna detta tack.
Mvh Ps älskar er EDDLER!
Anna Eddler Redaktör (Moderator)
Hej Thaimi,
uppgiften efterfrågade ”minsta heltalet” vilket är just $2$ då $x>1$. Så ditt svara böra vara $2$.
Ps. Kul att du gillar oss!
Marcus
Tal 6 behöver mer rätta alternativ, då det hänvisade sättet att skriva på i telet inte ens fungerar, ”x>=18”.
Anna Admin (Moderator)
Vi har problem med olikhetstecknet i systemet. Vi beklagar detta. Vi jobbar på den lösning.
Elise Nilsson
På fråga 8 ligger bokstäverna och figurerna fel.
Simon Rybrand (Moderator)
Tack för kommentar, vi fixar det!
Komvux Sundsvall Elev
På fråga 8 ligger svarsalternativen lite skevt. A har ingen bild under sig vilket gjorde att jag valde fel svarsalternativ.
Baldurn
I fråga 7 svarade jag tredje alternativet – alltså att ”−2<x<3" är störst.
Fel svar sade facit och gav mig en röd färg, och gav "−5<x<−2" en grön. Förundrad som jag var så ville jag läsa förklaringen till varför mitt svar var fel – men i förklaringen står det att mitt svar är rätt! Det är fel svarsalternativ inprogrammerat som rätt svar i den här frågan.
Simon Rybrand (Moderator)
Hej
Ja det var fel svar inprogrammerat i uppgiften där, tack för att du kommenterade detta! Det är korrigerat nu.
Caroline
Hej, undrar över det här då man dividerar något i ett ”x är större än eller mindre än….” tal..
Man ska väl vända på olikhetstecknet vid division?
/Carro
Simon Rybrand (Moderator)
Hej, Om du delar eller multiplicerar med negativa tal så behöver du vända på olikhetstecknet.
Caroline
Ja, men ni gör inte det i videon på något av talen där ni dividerar?
Simon Rybrand (Moderator)
I videon delar vi inte med negativa tal så då behöver vi inte vända på olikhetstecknet. Däremot borde nog denna video uppdateras med exempel på hur man gör det samt fördjupning kring att hantera olikhetstecken. Vi skall göra så att vi prioriterar det så att inga missförstånd uppstår.
Marcus Svensson
Handen i videon har sex fingrar.. 😛
Emelie
Hej! Finns det några videos i matte b kursen som förklarar exempel och tal på högre nivå inom varje område? Svårare exempel helt enkelt. Jag såg att det fanns en del MVG-exempel på genomgången av nationella proven B, men undrar om det finns några videos mer ingående i varje kapitell?
Simon Rybrand (Moderator)
Hej Emelie!
Ja det är framförallt i genomgångarna av de nationella proven som vi dyker ner i svårare uppgifter till kursen matematik B. Det finns fler problemlösningsgenomgångar till tex Matematik 1 och 2 i nuläget. Du är självklart varmt välkommen att kontakta oss om det är något speciellt område som du tycker att vi skall lägga upp mer genomgångar på!
/Simon
minst1.8
Olikheter och Linjära olikheter har samma video, ska det vara så?
Simon Rybrand (Moderator)
Hej, Nej det skall bara vara en video om linjära olikheter i kursen. Tydligen har den kommit med dubbelt av misstag i kursen. Vi ordnar det snarast
Endast Premium-användare kan kommentera.