Start / Bråk
Bråk
Allt om bråk
Ett bråk eller rationellt tal är ett tal som kan skrivas på formen a/b. Här kallas a för täljare och b för nämnare. Här samlar vi Eddlers alla lektioner om bråk och bråkräkning.
Våra lektioner om bråk
Här hittar du alla lektioner hos oss som handlar om bråk.
Bråktal, täljare och nämnare Gratis Videolektion
Matematik 1c, Matematik 1b, Matematik 1a, Matematik Årskurs 8, Matematik Årskurs 9, Matematik Högstadiet, Högskoleprovet matematik, Matematik 1Förlänga och förkorta bråk Videolektion
Matematik Årskurs 8, Matematik HögstadietBlandad form och bråkform Videolektion
Matematik Årskurs 8, Matematik HögstadietMinsta gemensamma nämnare (MGN) Gratis Videolektion
Matematik Årskurs 8, Matematik HögstadietJämföra bråk Videolektion
Matematik Årskurs 8, Matematik HögstadietBråk på tallinjen Videolektion
Matematik Årskurs 8, Matematik HögstadietAddition och subtraktion av bråktal Videolektion
Repetition inför Matematik 2, Repetition inför Matematik 1, Matematik 1c, Matematik 1b, Matematik 1a, Matematik 3c med Avancera I, Matematik Årskurs 8, Matematik Årskurs 9, Matematik Högstadiet, Högskoleprovet matematik, Matematik 1Tillämpning addition och subtraktion av bråk Videolektion
Matematik Årskurs 8, Matematik HögstadietMultiplicera bråk Videolektion
Repetition inför Matematik 2, Repetition inför Matematik 1, Matematik 1c, Matematik 1b, Matematik 1a, Matematik 3c med Avancera I, Matematik Årskurs 8, Matematik Årskurs 9, Matematik Högstadiet, Högskoleprovet matematik, Matematik 1Dividera bråk Videolektion
Repetition inför Matematik 2, Repetition inför Matematik 1, Matematik 1c, Matematik 1b, Matematik 1a, Matematik 3c med Avancera I, Matematik Årskurs 8, Matematik Årskurs 9, Matematik Högstadiet, Högskoleprovet matematik, Matematik 1Multiplicera och dividera bråktal Videolektion
Tillämpning multiplikation och division av bråk Videolektion
Matematik Årskurs 8, Matematik HögstadietMer om bråk
Här sammanfattar vi alla våra lektioner om bråk.
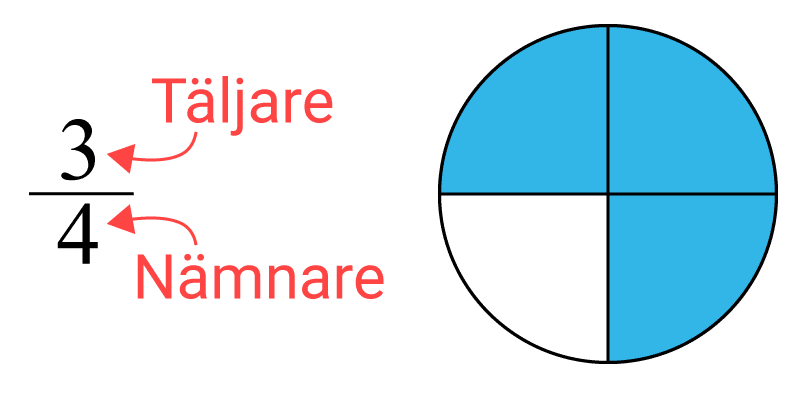
Ett bråktal är ett tal som du skriver på formen a/b där a och b är heltal. Bråktal kallar vi också för rationella tal (ℝ). Talet a kallas för täljare och talet b kallas för nämnare. Ett bra sätt för dig att komma ihåg detta är att tänka att ”t som i tak och täljare” och ”n som i nämnare och nere”. Lär dig mer om vad bråktal är här.
Grunder i att hantera bråktal
Det finns ett antal olika grundläggande kunskaper om bråktal som är viktiga att du lär dig innan du börjar räkna med bråktal.
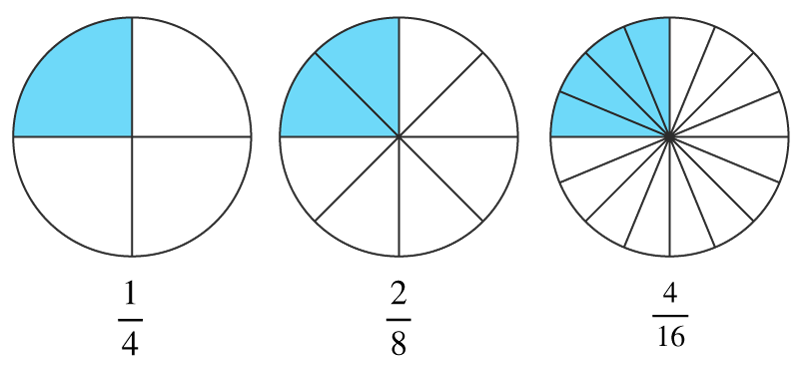
Förlänga och förkorta
Det första du behöver lära dig är att kunna förlänga och förkorta bråktal. När du förlänger eller förkortar bråktal så multiplicerar eller dividerar bråktalets täljare och nämnare med samma tal. Bråktalet är fortfarande lika stort men har andra täljare eller nämnare.
Minsta gemensam nämnare
När du skriver två eller flera bråktal med minsta gemensam nämnare (MGN) så söker du den nämnare som du kan dela med bråktalens alla nämnare. Med andra ord den minsta nämnare som alla bråktalen kan förlängas eller förkortas till.
När du har lärt dig minsta gemensamma nämnare så blir det också enklare att jämföra bråktals storlek och förstå hur du placerar ut bråktal på tallinjen.
Blandad form och bråkform
I bråktalet är skrivet på bråkform. Dessutom är täljaren större än nämnaren. Därför kan vi skriva om bråktalet till blandad form. Om vi skriver ett bråktal på blandad form så skriver man hur många hela bråket motsvarar följt av resten av andelarna. Därför gäller att
(En hel och fyra åttondelar)
Lär dig mer om blandad form och bråkform här.
Att jämföra bråktals storlek
När du kan skriva om tal så att de står på minsta gemensam nämnare så blir det enklare att jämföra bråk. Då kan du först skriva om så det står på gemensam nämnare och då är det största bråktalet det tal som har störst täljare.
Bråk och de fyra räknesätten
När du skall addera, subtrahera, multiplicera och dividera bråktal så är det viktigt att du lärt dig grunderna som vi beskriver här ovan. Därefter blir det enkelt att utföra de fyra räknesätten.
Vid addition och subtraktion av bråk behöver du ofta först förlänga eller förkorta till samma nämnare. Sedan adderar eller subtraherar täljarna med varandra. Exempelvis kan en addition av bråk se ut på följande vis.
När du multiplicerar bråk eller dividerar bråk så är det följande regler som du använder dig av:
Multiplikation:
Division:
Tillämpningar av bråk
Bråkräkning kan användas för att lösa olika typer av problem. Exempelvis hur stor andel något är av en helhet eller hur mycket kvar vi har av något efter en andel i bråkform har förbrukats. För att träna på sådan problem gå till:
Höj dina resultat i matematikkursen!
- Högstadiet och hela gymnasiet.
- Mer än 600 supertydliga videos.
- Träna inför ditt nationella prov.
- Dessutom Fysik 1, programmering och högskoleprovet.
Nyheter
Nya lektioner med tips om provdelen KVA, se mer i vår Högskoleprovskurs.
Populära kurser
Åk 9
66 lektioner

Matematik 2b
92 lektioner

Matematik 3c
67 lektioner

Högskoleprovet
71 lektioner

Matematik basår
95 lektioner

Fysik 1
92 lektioner
Våra användare gillar oss!
Populära lektioner
Räta linjens ekvation Gratis
Matematik 2
Ekvationslösning
Matematik 1
Vad är Algebra?
Matematik 1
Beteckningen f(x)
Matematik 1
Ohms lag Gratis
Fysik 1
Förenkla algebraiska uttryck
Matematik 1
Tallinjen Gratis
Matematik 1
Vad är funktioner
Matematik 1
Kort division - dividera med uppställning
Matematik högstadiet
Enhetscirkeln Gratis
Matematik 3
Få tillgång till allt för
endast 99 kr/mån
Över 600 lektioner. Ingen bindningstid. Avsluta när du vill.
Prova gratis