Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
- k = riktningskoefficienten eller linjens lutning.
- m = y – värdet där linjen skär y – axeln, dvs där x = 0.
I den här lektionen går vi inte igenom ny teori. Vi exemplifierar itället hur man kan förstå och jobba med olikheter för att beskriva områden i planet.
Det kan det vara bra att ha förkunskaper om räta linjens ekvation för att kunna följa alla resonemang. Framförallt att förstå räta linjer skrivna på formen $ y = kx + m $ där
- k = riktningskoefficienten eller linjens lutning.
- m = y – värdet där linjen skär y – axeln, dvs där x = 0.
Ligger halvplanet över eller under linjen?
Här kommer ett trick, som kanske kan hjälpa dig om du känner dig osäker på hur vida halvplanet ligger över eller under linjen.
Lägg din högra hand på högkant längst upp på koordinatsystemets övre kant. Lillfingret ska vara parallellt med xx -axeln och handflatan öppen nedåt mot koordinatsystemets nedre kant. För sedan din högra hand ovanifrån mot linjen och låt den ”landa” på linjen. Området som hamnar under handflatan är då under linjen och motsvarar alltså att yy -värdena är mindre än linjen. För området ovanför handen gäller att halvplanet är över linjen, vilket i sin tur med för att yy -värdena är större än linjen.
För linjen x=ax=a gäller i stället att du för handen från höger mot linjen och avgör på så sätt om det markerade halvplanet är på ovansidan av handen, vilket motsvarar större värden eller på undersidan av handflatan och motsvarar mindre värden.
Utöver detta bör du observera om linjen är heldragen och tillhör halvplanet eller streckad och inte tillhör halvplanet, för att kunna teckna korrekt olikhet.
≤,≥≤,≥ olikheterna är slutna. Då tillhör alla punkter på linjen halvplanet. Linjen som delar planet är heldragen.
<,><,> olikheterna är öppna. Då tillhör ingen av punkterna på linjen halvplanet. Linjen som delar planet är streckad.
Hur kan man avgöra om en punkt tillhör halvplanet?
Vi kan undersöka det grafiskt genom att rita upp linjen och plottar ut punkten och på så sett se om den tillhör halvplanet.
Men vi kan även undersöka det algebraiskt. Ofta går det snabbare än att rita halvplanet i ett koordinatsystem.
Genom att sätt in punktens koordinater i olikheten och se om den uppfylls kan vi avgöra hur vida den tillhör halvplanet eller ej. Uppfylls olikheten tillhör punkten planet. Om inte tillhör den ej halvplanet.
Tex skulle vi kunna undersöka om punkten (4, −1)(4, −1) tillhör halvplanet som beskrivs av olikheten y<y< 2x−32x−3 genom att sätta in värdet på xx och yy för punkten i VLVL och HLHL . Punkten har ju har xx -värdet fyra och yy -värdet minus ett. Det skulle i vår olikhet y<y< 2x−32x−3 ge att
VL=−1VL=−1 och HL=2⋅4−3=5HL=2·4−3=5
vilket i sin tur leder till att
VL<VL< HLHL då −1<5−1<5
Detta stämmer överens med vad den den givna olikheten anger och därför tillhör punkten (4,−1)(4,−1) halvplanet.
Tips när du ska markera ett område
Då den linjära olikheten som definierar ett halvplan, inte uttrycks på så sätt att den är lik räta linjens kk -form, alltså att variabeln yy är själv i ena ledet, bör den skrivas om så att det blir lättare att avgöra punkternas relation till halvplanet.
Till exempel underlättar det jobbet med att markera halvplanet som beskrivs av olikheten y+2x−3≤0y+2x−3≤0 om man först skriver om olikheten så här.
y+2x−3≤0y+2x−3≤0 Addera båda leden med 33
y+2x≤3y+2x≤3 Subtraheta båda leden med 2x2x
y≤−2x+3y≤−2x+3
Nu kan man lättare rita linjen som delar planet i två halvor!
Exempel i videon
- Markera ett område i planet som kan beskrivas av y < -x + 3.
- Ligger punkten (-2, 0) i det halvplan som beskrivs av y +2x + 2 ≤ 0
Kommentarer
e-uppgifter (8)
1.
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
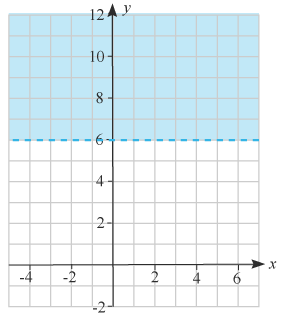 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
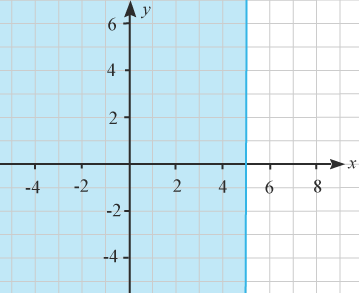 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
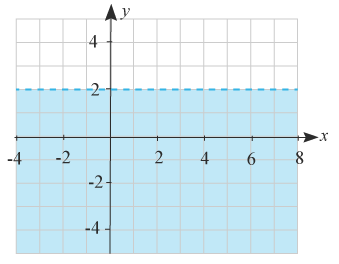 Svar:Ditt svar:Rätt svar: y<2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: y<2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K I vilken av figurerna är halvplanet som motsvarar olikheten y≤x+2y≤x+2 markerad med blått?
A.
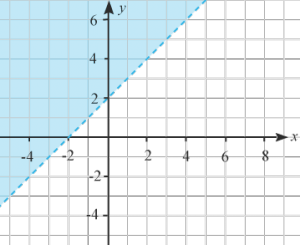
B.
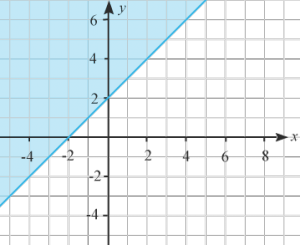
C.
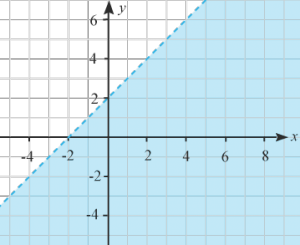
D.
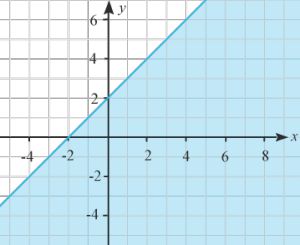 Svar:Ditt svar:Rätt svar: Figur D.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: Figur D.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
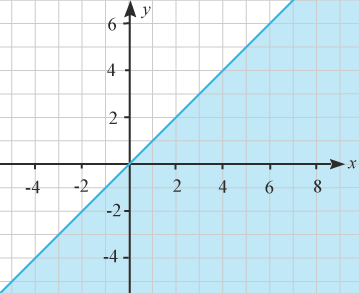 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B 1 P PL M R K I figuren är ett halvplan markerat med blått, vilken olikhet beskriver detta halvplan?
 Svar:Ditt svar:Rätt svar: y>−3x+6(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: y>−3x+6(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(1/0/0)E C A B P 1 PL M R K Vilken av följande punkter ligger i området som beskrivs av y>−2x+3y>−2x+3 ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(1/0/0)E C A B P 1 PL M R K Ligger punkten (0,0)(0,0) i halvplanet som begränsas av y≥xy≥x ?
Svara ja eller nej, men öva även på att motivera ditt svar algebraiskt och grafiskt.
Svar:Ditt svar:Rätt svar: Ja.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (1)
9. Premium
(1/1/0)E C A B P 1 PL M R 1 K Vilken av följande punkter ligger i området som beskrivs av olikheten y<y< x−2x−2 ?
Träna även på att motivera ditt svar grafiskt och algebraiskt.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Judith Lysell
Hej!
Även här får man fel för rätt svar på fråga 3 och fråga 6.
Jag har testat att skriva det på lite olika sätt, men det blir ändå fel.
Hanna Lundqvist
Tycker att det hade varit bra att här beskriva att uppgiften med punkten i videon går betydligt snabbare att lösa algebraiskt, upplever att eleverna behöver förstå den aspekten av hur en olikhet fungerar och inte alltid gör det. Alltså inte ta bart den grafiska lösningen bara komplettera med den algebraiska.
Även att rita upp den räta linjen enbart med hjälp av k-värdet som också är mer tidseffektivt och tyder på, eller kan ge, en djupare förståelse av funktionens form.
Simon Rybrand (Moderator)
Hej Hanna och tack för din kommentar!
Vi tar med oss detta i framtida utveckling av lektionen.
Mattefreak
Jag sitter fast hårt på denna och har snart nationella, behöver bli klok på detta snarast. HJÄLP!
Funktionen V(x.y)= 3x-2y är definierad på området i xy-planet som bestäms av
x >_0
0 <_y <_ -x+5
1. Rita upp en del av området som beskrivs av olikheterna.
2. Bestäm funktionen V:s maximala och minimala värde i detta område.
3. Fungerar det att bestämma max/min värde för funktionen V (x,y)= X^2-3y med samma metod?
Simon Rybrand (Moderator)
1. Rita ut linjen y=−x+5 och det område som du söker är alla värden under denna linje och till höger om y-axeln och över x-axeln.
2. Här måste du testa hörnen, dvs (0; 0), (0, 5) och (5, 0)
Andrea Olsson
Hej!
När du ska skriva om uttrycket y + 2x + 2 <_ 0, varför subtraherar du med -2? Det framgår inte varför du subtraherar med 2… Är det för att något + 2 = 0, och då blir det -2?
Mvh
Andrea
Simon Rybrand (Moderator)
Hej
Anledningen till att jag subtraherar med 2 där är för att skriva om olikheten så att den liknar y=kx+m, dvs vi vill få y ensamt på ena sidan av olikhetstecknet. Så där subtraherar jag med 2 för att få bort +2 på vänstra sidan då +2−2=0
Endast Premium-användare kan kommentera.