Författare: Simon Rybrand
Simon Rybrand  Anna Karp
Anna Karp
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
I den här lektionen lär du dig vad en integral är och hur vi använder insättningsformeln som bygger på integralkalkylens fundamentalsats.
Integralens definition
Integraler kan förenklat beskrivas som en summa av oändligt många förändringar. Ett vanligt sätt att bestämma integralens värde är att beräkna arean mellan en funktions graf och xx -axeln. I de fall där arean inte motsvarar en geometrisk figur som vi redan har en given formel för, kan arean beräknas genom att dela upp arean i oändligt många rektanglar, vars enskilda areor summeras.
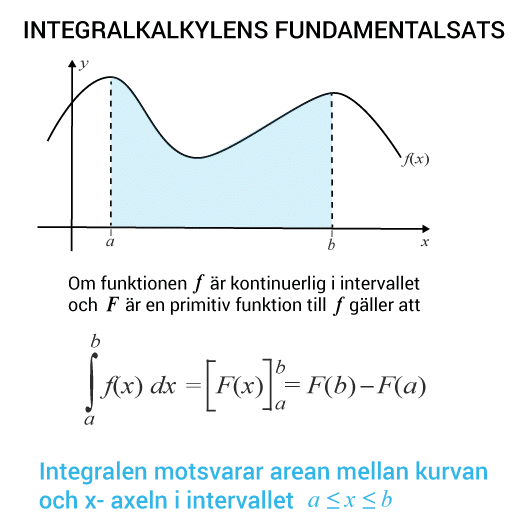
Ibland kallas summa av alla rektanglarna för en Riemannsumma efter matematikern Berhard Riemann. Han var en tysk matematiker bland andra, som har spelat stor roll för utvecklandet av integralberäkningar.
Symbolen ∫∫ infördes av en annan tysk matematiker som jobbade med beräkningar av integraler, nämligen Gottfried Willhelm von Leibniz. Symbolen är en dåtida bokstav för s:et i summa.
Sist i denna lektion går vi igenom betydelsen av de olika tecknen i satsen. Men först tittar vi på vad satsen motsvarar.
Från en summa av areor till en integral
Här kommer en beskrivning av hur arean under kurvan och integralen hänger ihop. Metoden kallas för Mittpunktmetoden. Först delas arean in i ett antal rektanglar med basen △x△x.
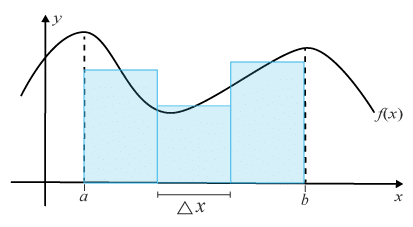
Höjden på varje rektangel sätts till f(xi)ƒ (xi), där xixi motsvarar xx-värdet i mitten av varje rektangel. Vi beräkna arean på varje rektangel som höjden f(xi)ƒ (xi) gånger basen △x△x , och får en generell beskrivning av varje rektangels arean till f(xi)⋅△xƒ (xi)·△x.
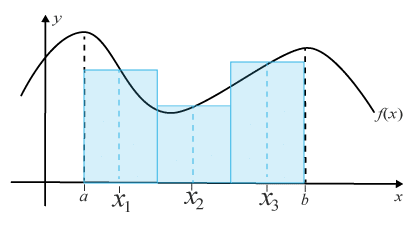
För att få värdet till var rektangels area sätter vi nu in det indexvärde varje xixi antar för de olika rektanglarna. Rektangeln längst till vänster har index i=1i=1 vilket ger arena f(x1)⋅△xƒ (x1)·△x. Rektangeln nästa längst till vänster har index i=2i=2 vilket i sin tur ger värdet f(x2)⋅△xƒ (x2)·△x. Så fortsätter detta mönster för varje rektangel.
Summerar vi dessa rektanglars areor får vi att arean AA mellan kurvan och xx -axeln i intervallet a≤x≤ba≤x≤b är
A≈f(x1)⋅△x+f(x2)⋅△x+f(x3)⋅△xA≈ƒ (x1)·△x+ƒ (x2)·△x+ƒ (x3)·△x
Detta ger ett ganska grov närmevärde, då vi ser att rektanglarnas areor inte stämmer så bra överens med den faktiska arean mellan kurvan och xx -axeln. För att minska felet delar vi därför upp arean i rektanglar med mindre och mindre bas △x△x.
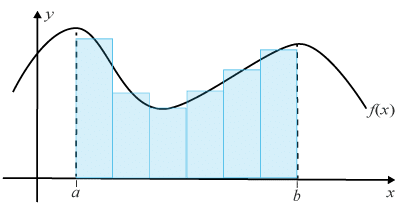
När vi till slut fått väldigt många rektanglar, effektiviserar vi beräkningen genom att skriva om summan med hjälp av symbolen sigma, så här
Σi=1nf(xi)⋅△xΣi=1nƒ (xi)·△x
vilket alltså motsvarar summan av nn stycken rektanglars areor. När basen △x△x blir mindre och mindre kommer antalet rektanglar att bli fler och fler.
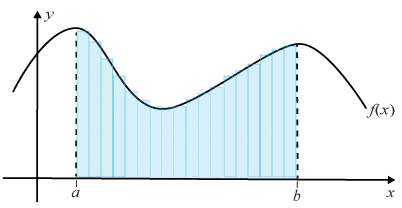
När antalet rektanglar blir oändligt många, när n→∞n→∞, får vi ett gränsvärde på summan som kan beskrivas med
n→∞lim Σi=1nf(xi)⋅△xΣi=1nƒ (xi)·△x
Det är detta gränsvärde som fått en egen symbol och betecknas med
a∫bf(x)dx
där ∫∫ härstammar från bokstaven s som i summa och är tecknet för integralen och dxdx är skrivsättet som här motsvarar att △x△x går mot noll.
Och så har vi här nu fått en ny metod för att beräkna arean mellan kurvan och xx-axeln!
Integralkalkylens fundamentalsats
Utifrån ovanstående genomgång av beräkning av areor med mittpunktsmetoden och tidigare kunskap kring de primitiva funktioner ska vi nu försöka landa i den sats som vi i denna kurs använder för att bestämma en integrals värde algebraiskt.
Då vi kommer att ta hjälp av de primitiva funktionerna för att lösa uppgifterna framåt, repeterar vi följande.
En kontinuerlig funktion FF i intervallet a≤a≤x≤x≤ bb är en primitiv funktion till funktionen fƒ i samma intervall om F′(x)=f(x)F’(x)=ƒ (x)
Med andra ord. Om derivata till FF är lika med funktionen fƒ är FF en primitiv funktion till fƒ .
Innan vi i kommande lektion visar hur vi rent praktiskt beräknar integraler algebraiskt ska vi titta på den sats vi kommer använda vid beräkningen.
Den kallas Integralkalkylens fundamentalsats och kan delas in i två delar, där den andra delen kommer vara den vi refererar till när vi gör beräkningar med satsen framöver.
Satsen säger att för den kontinuerliga funktionen fƒ gäller följande i intervallet a≤a≤x≤x≤ bb.
Funktionen F(x)=∫axf(t)dtF(x)=∫axƒ (t)dt är en primitiv funktion till fƒ i intervallet a≤a≤x≤x≤ bb.
Med andra ord gäller att F′(x)=f(x)F’(x)=ƒ (x). Vidare gäller även att
Om FF är en primitiv funktion till fƒ i intervallet a≤a≤x≤x≤ bbär
∫abf(x)dx=F(b)−F(a)∫abƒ (x)dx=F(b)−F(a)
Den senare kallas även insättningsformeln.
Då likheten ∫abf(x)dx=[F(x)]ab∫abƒ (x)dx=[F(x)]ab ger ett annat sätt att beteckna integralens värde, följer att [F(x)]ab=F(b)−F(a)[F(x)]ab=F(b)−F(a).
Satsen innehåller, kanske för dig, många nya symboler och tecken så här följer en förklaring av de olika delarna.
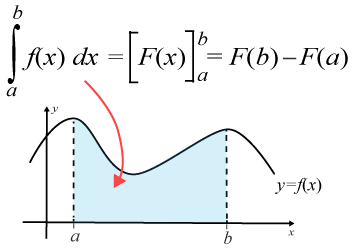
- ∫ är integraltecknet
- aa är den undre integrationsgränsen, som begränsar arean åt vänster
- bb är den övre integrationsgränsen, som begränsar arean åt höger
- f(x)ƒ (x) är integranden, som är den funktion vars graf begränsar arenan uppåt
- xx i skrivningen dxdx anger integrationsvariabeln
- dxdx anger att beräkningen ska ske med avseende på förändring i xx -led
- F(x)F(x) är en primitiv funktion till f(x)ƒ (x)
Själva beräkningen av integralen genomförs alltså genom att sätta in den över gränsen bb i den primitiva funktionen till f(x)ƒ (x) och subtraherar med värdet du får när du sätter in den undre gränsen aa i den primitiva funktionen F(x)F(x).
Här en annan överblick som kanske kan hjälpa dig vid inlärning av de olika begreppen.
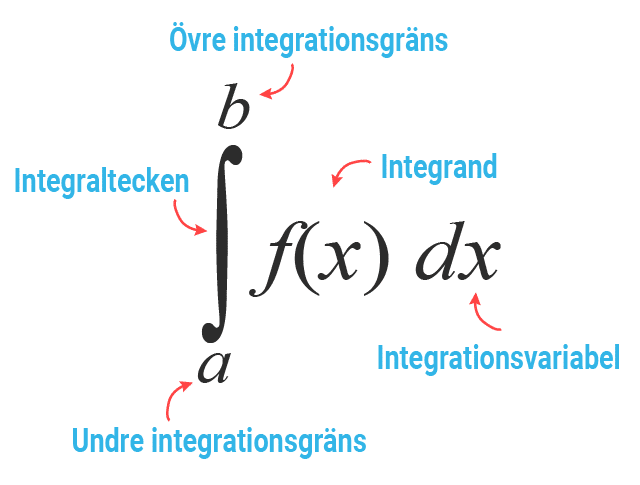
I nästa lektion går i vi igenom exakt hur du kan beräknar integralen algebraiskt med hjälp av denna sats.
Exempel i videon
- En fotbollsspelare kastar ett inkast. Hastigheten vm/s de första två sekunderna efter inkastet kan beskrivas med hjälp av funktionen v(t)=4−t2 där t är tiden i sekunder. Hur lång sträcka har bollen rört sig under de två första sekunderna?
- Beräkna 0∫2(4−t2)dt
Kommentarer
e-uppgifter (15)
1.
(1/0/0)E C A B 1 P PL M R K Vilket av följande tecken betecknar en integral?
Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...2.
(1/0/0)E C A B 1 P PL M R K Vilket påstående stämmer bäst för integralen?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B 1 P PL M R K Det skuggade områdets area på bilden kan beräknas med integralen 1∫40,5x+2dx.
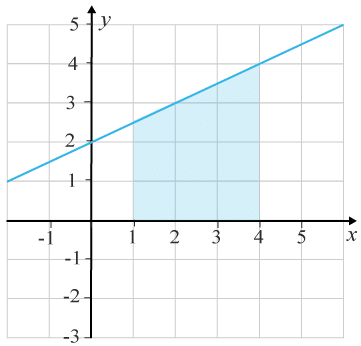
Vilken är den övre integrationsgränsen för integralen?
Svar:Ditt svar:Rätt svar: 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K Det skuggade områdets area på bilden kan beräknas med integralen 1∫40,5x+2dx.

Vilken är den undre integrationsgränsen för integralen?
Svar:Ditt svar:Rätt svar: 1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B 1 P PL M R K Ange övre integrations gränsen till integralen −2∫32x−5dx.
Svar:Ditt svar:Rätt svar: 3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(1/0/0)E C A B 1 P PL M R K Figuren beskriver grafen till f(x)=−x2+2x+3ƒ (x)=−x2+2x+3.
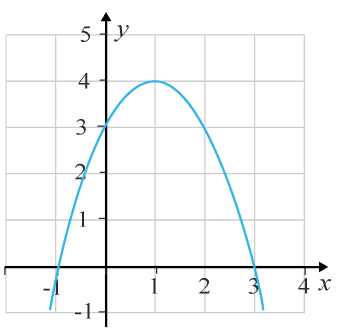
Vad beräknar du med integralen 1∫2(−x2+2x+3)dx?
Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...7. Premium
(2/0/0)E C A B 1 P 1 PL M R K Grafen till funktionen y=f(x)y=ƒ (x) är utritad i i koordinatsystemet.
Använd figuren och uppskatta −1∫3f(x)dx
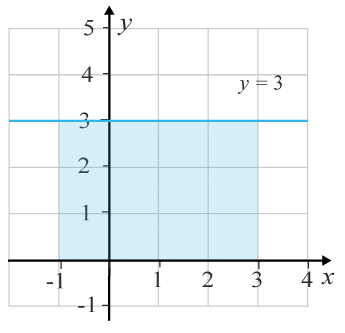 Svar:Ditt svar:Rätt svar: 12(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 12(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...8. Premium
(2/0/0)E C A B 1 P 1 PL M R K Det skuggade områdets area kan beräknas med en integral.
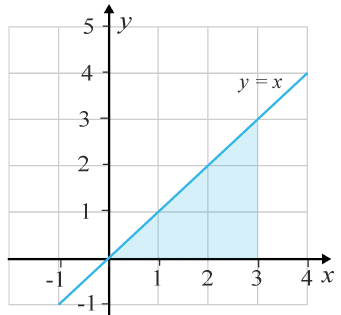
Beräkna integralen värde.
Svar:Ditt svar:Rätt svar: 4,5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...9. Premium
(1/0/0)E C A B 1 P PL M R K Grafen till funktionen y=f(x)y=ƒ (x) är utritad i i koordinatsystemet.
Använd figuren och uppskatta 1∫4f(x)dx
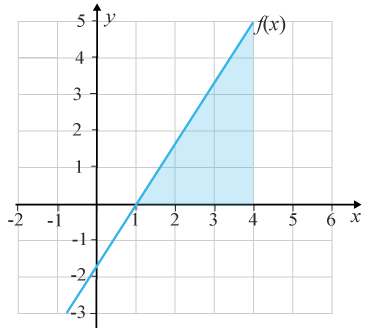 Svar:Ditt svar:Rätt svar: 7,5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 7,5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...10. Premium
(1/0/0)E C A B 1 P PL M R K Grafen till funktionen y=f(x)y=ƒ (x) är utritad i i koordinatsystemet.
Använd figuren och uppskatta 1∫4f(x)dx
 Svar:Ditt svar:Rätt svar: 9,75(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 9,75(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...11. Premium
(2/0/0)NPE C A B P PL 2 M R K Figuren visar grafen till en funktion fƒ . Grafen går genom de tre markerade punkterna.

Bestäm ∫−26f(x)dx∫−26ƒ (x)dx
Svar:Ditt svar:Rätt svar: 27,5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...12. Premium
(1/0/0)E C A B 1 P PL M R K Vilken integral kan du använda för att beräkna arean av det markerade området?
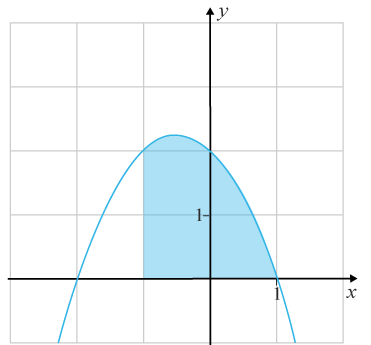 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...13. Premium
(2/0/0)E C A B 1 P PL M R 1 K Ange den figur vars markerade area motsvarar integralen
∫01 x3−3x2+x+1 dx∫01 x3−3x2+x+1 dx
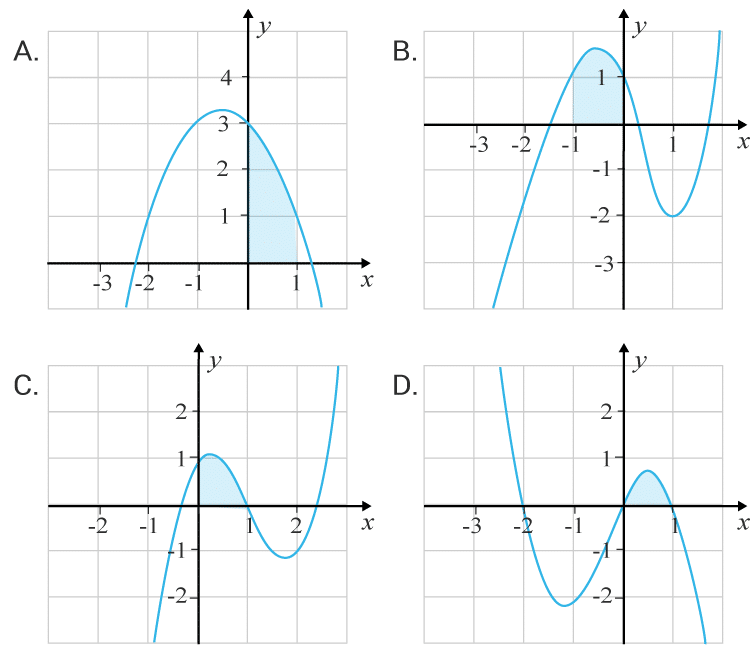
Träna på att motivera ditt svar.
Svar:Ditt svar:Rätt svar: Figur C(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...14. Premium
(1/0/0)E C A B P 1 PL M R K När vi beräknar integraler introducerar vi ett nytt skrivsätt.
Vilket alternativ är ett korrekt skrivsätt för fortsatt av beräkning av ∫14 3x2dx∫14 3x2dx ?Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...15. Premium
(1/0/0)E C A B 1 P PL M R K Grafen till funktionen y=f(x)y=ƒ (x) är utritad i i koordinatsystemet.
Använd figuren och uppskatta −2∫2f(x)dx
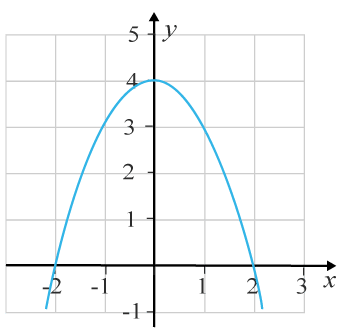 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Integraler - introduktionRättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (1)
16. Premium
(0/1/0)NPE C A B 1 P PL M R K Grafen till funktionen fƒ bildar en kvartscirkel i första kvadranten.
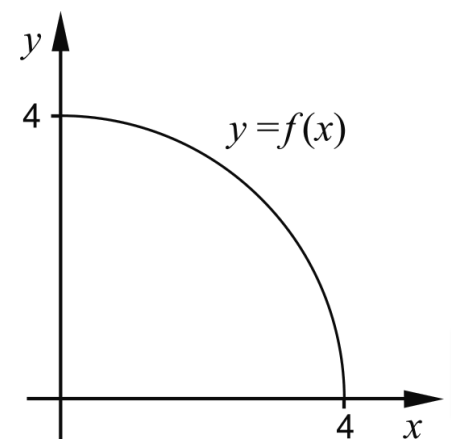
Bestäm 0∫4 f(x) dxƒ (x) dx . Svara exakt.
Svar:Ditt svar:Rätt svar: 4π(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Ebelia Perlkvist
På sista frågan valde jag rätt svarsalternativ enligt er lösning till uppgiften men fick ”fel”. Det verkar som att ni inte har markerat vilket alternativ av de 4 som är rätt.
Yosefd
Hej! förstår inte riktigt varför 3x^1 blir 3x^2/2 ibland så blir det bara x^3/3 sen undrar jag hur man ska tänka när det är e^-0.4X eller e^2x, e^-0.5 tex. Har lite svårt för detta.
Simon Rybrand (Moderator)
Hej
Du kan egentligen hela tiden gå på metoden att du upphöjer exponenten med ett steg och även delar med exponenten. Det kommer att bli rätt då. Det du kommer att märka är att du sedan kan förenkla uttrycket så att den primitiva funktionen blir enklare. Två exempel på detta:
3x har den primitiva funktionen 23x2 (går inte att förenkla mer)
3x2 har den primitiva funktionen 33x3=x3 (Här gick det att förenkla då 3/3=1)
Jonsar
Bästa sidan för matte jag någonsin sett! Har alltid haft svårt att följa med på matte lektionerna men denna sida gör det flera gånger enklare att förstå. Tackar!
Simon Rybrand (Moderator)
Kul att höra!
Fortsatt lycka till med pluggandet!
Leila
Hej!
Jag behöver hjälp med den här frågan,tack!
En area begränsas av funktionen y= 4e^4x + 2 , linjen x= -1 samt koordinataxlrna.
Jag försöker skicka biden av koordinatgrafen…
Simon Rybrand (Moderator)
Hej,
Tror att jag behöver se en bild eller veta i vilken kvadrant vi befinner oss för att kunna lösa denna korrekt.
fatima94
Hej! jag behöver hjälp med att lösa denna uppgiften :
En sten kastas rakt upp i luften har hastigheten v(t)=24-9,8t. Tiden anges i sekunder och hastigheten i m/s.
a) hur högt har föremålet stigit efter 1 sek i luften?
b) hur högt stiger föremålet innan det vänder?
c) Har funktionen v(t) några begränsningar? om ja, ange dessa.
Simon Rybrand (Moderator)
Hejsan, här kastas alltså en sten upp i luften och kommer sedan att ”dras” tillbaka igen mot marken av tyngdkraften. Hastigheten kommer här att minska mot 0 tills den har nått vändpunkten och sedan att vara negativ tills den landar igen.
a) Här vet du t = 1 och skall beräkna s som ges av integralen från t = 0 till t = 1. Dvs
0∫1(24−9,8t)dt
b) Här kan du lösa ekvationen
v(t) = 0 ⇔
24-9,8t=0
Dvs när hastigheten är 0 så har du en vändpunkt för stenen.
c)
v(t) kan ju aldrig vara större än 24. Sedan så kommer stenen att landa igen. Så här behöver du ta reda på efter hur lång tid som den har landat och vilken hastighet som den har (kommer att vara negativ) i landningsögonblicket.
johannawallstrom
Hej!
på fråga 3 räknade jag x^3/3 – x^3/3 +x=3
tog 3*1,5=4,5a.e
Hade jag tur eller hade jag också rätt??
Simon Rybrand (Moderator)
Hej Johanna, har lite svårt att följa hur du tänkte här, i det här fallet så är det inte en ekvation som behöver lösas utan en integralberäkning så min rekommendation är att du försöker att göra liknande beräkningar med hjälp av integralkalkylens fundamentalsats så att det inte blir fel i framtida beräkningar.
Endast Premium-användare kan kommentera.