Integraler

Integraler är en matematisk operation som du utför på en funktion. Med hjälp av en integral beräknar du exempelvis arean mellan en kurva och x-axeln i ett intervall. Därför kan du använda integralen till att beräkna olika typer av areor. Dessutom kan du använda dem för att beräkna volym, längd, hastighet, acceleration och kraft.

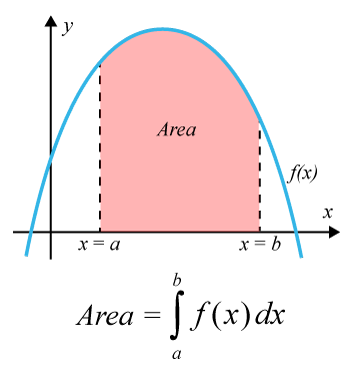
Nedan går vi igenom de olika teoriområden som är viktiga för att du skall förstå integraler. Med andra ord kan du använda texterna nedan för att få en överblick av integraler.

Primitiva funktioner

En viktig förkunskap för att förstå integraler är primitiva funktioner. Det beror på att dessa funktioner används vid beräkningar av integraler.

En primitiv funktion F(x) är den funktion vars derivata är lika med funktionen f(x). Som ett resultat av det så kallas primitiva funktioner ofta för ”baklängesderivata” eller ”antiderivata”.

Integralkalkylens fundamentalsats

Den matematiska satsen som du använder för att beräkna integraler kallas för integralkalkylens fundamentalsats. Med hjälp av den beräknar du integralens värde. Därför är det den som du använder när du skall beräkna en area eller en hastighet i en tillämpning. Själva satsen säger följande:

$\int\limits_a^b f(x) dx = \left[ F(x) \right]_a^b = F(b) – F(a)$

Denna sats använder du i alla former av beräkningar med integraler. Så därför är det mycket viktigt att du lär dig hur du använder metoden.

Areor

Integraler använder du alltså för att exempelvis beräkna areor. Du kan beräkna areor under kurvor och areor mellan kurvor.

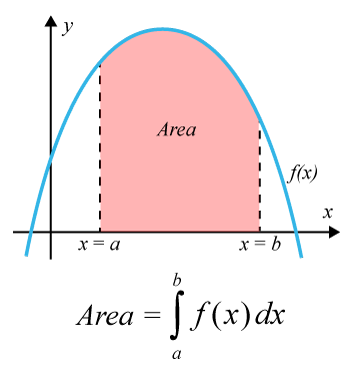
Tänk också på att du behöver känna till om en kurva går under x-axeln. Som ett resultat av att kurvan går under x-axeln så behöver du sätta ett minustecken framför integralen. Särskilt viktigt är det att du använder det när du beräknar integraler med trigonometriska funktioner.

Volymintegraler

Dessutom kan du använda integraler för att beräkna olika typer av volymer. Exempelvis använder du skivmetoden för att beräkna sådana volymer.

Partiell integration

Avslutningsvis avslutas gymnasiets innehåll om integralkalkyl med partiell integration i Matematik 5. Ordet partiell betyder ungefär ”en del av” och idén här är att dela upp integralen i olika delar och på det viset hitta den primitiva funktionen.