
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 4
/ Integraler
Volymintegraler och Cylindriska skal
Metoden med cylindriska skal
Metoden går ut på att man kan dela upp vissa kroppar i cylindriska skal/snitt och där dessa skals volym kan beräknas på samma sätt som man beräknar volymen för ett rätblock (låda).
Ett exempel på detta kan vara funktionen $f(x)=8x-4x^2 $ som skapar volym i bilden nedan om vi låter denna rotera runt y-axeln.
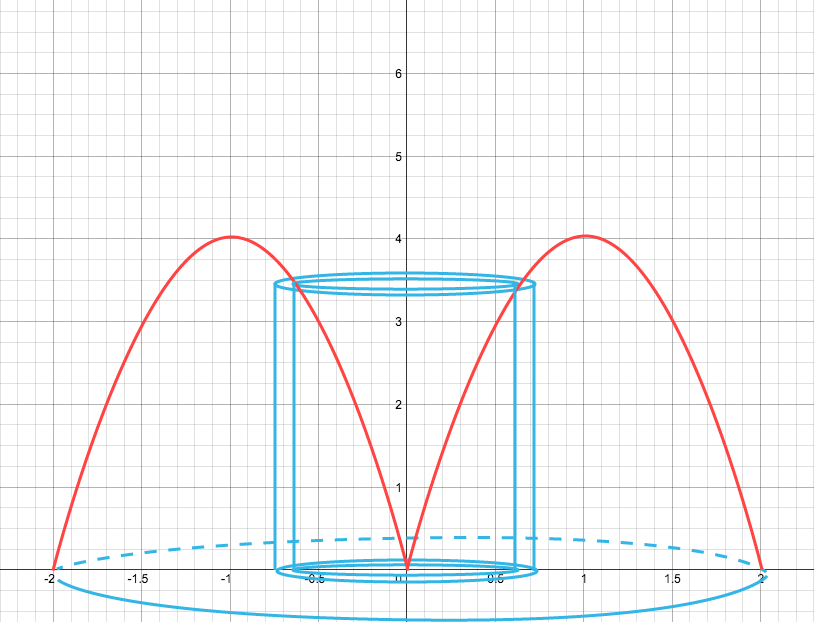
Inne i volymen kan ett cylindriskt skal skapas som kan liknas vid ett rör och det här cylindriska skalet kan ”vecklas” ut till ett rätblock. Rätblocket kommer att ha volymen
$ 2 \pi ⋅ r ⋅ y⋅ Δx = $ $ 2 \pi x f(x) Δx = $ $ 2 \pi (x (8x-4x^2)) Δx = $ $ 2\pi ( 8x^2-4x^3) Δx $.
Sedan kan volymen för alla cylindriska skal beräknas genom integralen
$ \int\limits_0^2 2 \pi (8x^2-4x^3) dx $
Exempel i videon
- Beräkna volymen som skapas då vi låter $ y=x-x^2 $ rotera runt y-axeln och begränsas av x-axeln.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (4)
-
1. Premium
Beräkna volymen som skapas då vi låter $f(x)=2x-x^2$ƒ (x)=2x−x2 rotera kring $y$-axeln och begränsas av $x$-axeln.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
Linjerna $y=1$y=1 , $x_1=2$x1=2 och $x_2=3$x2=3 bildar tillsammans med $x$-axeln ett slutet område i första kvadranten. Använd cylindriska skal och beräkna volymen som skapas då detta område roteras kring $y$-axeln.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
Beräkna volymen som skapas då vi låter $f(x)=3x^2-x^3$ƒ (x)=3x2−x3 rotera kring $y$-axeln och begränsas av $x$-axeln.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
Använd metoden med cylindriska skal och beräkna volymen som skapas då det färgade området roteras runt $y$y-axeln.
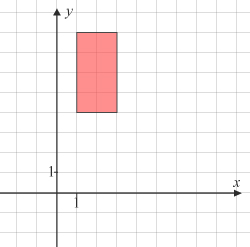
Försök sedan att komma på ett alternativt (och gärna enklare) sätt att bestämma rotationsvolymen.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
c-uppgifter (3)
-
5. Premium
Beräkna volymen som bildas då funktionen $y=\sqrt{x}+1$y=√x+1 roteras kring $y$-axeln i intervallet $1\le x\le4$1≤x≤4 .
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
6. Premium
Funktionerna $y_1=2x$y1=2x och $y_2=\frac{x^2}{2}$y2=x22 bildar ett slutet område i första kvadranten. Beräkna volymen som skapas då detta område roteras kring $y$-axeln.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
7. Premium
Funktionen $y=\frac{x^2}{2}-2$y=x22 −2 och linjen $x=4$x=4 bildar ett slutet område i första kvadranten. Beräkna volymen som skapas då detta område roteras kring $y$-axeln.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
a-uppgifter (1)
-
8. Premium
Beräkna volymen som bildas då funktionen $y=sin\left(x\right)$y=sin(x) roteras kring $y$-axeln i intervallet $0\le x\le2\pi$0≤x≤2π.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...

Amal Hussein
Tack så mycket 🙂
Bestäm volymen av den kropp som bildas då området som begränsas av y=x^2 och y=x roterar runt linjen x= -3?
Kan du hjäpa mig med denna med?
Amal Hussein
Bestäm volymen av den rotationskropp som bildas om arean under kurvan f(x) 1/x – 0,1 i första kvadranten roterar runt x-axeln då x>1?
Har fastnat på denna beräkningen:/
Simon Rybrand (Moderator)
Volymen för en skiva är:
$ \pi·r^2·Δx=\pi·(1/x-0,1)^2·Δx $
Sedan beräknade volymen för alla skivor, dvs volymen från x>1 till a=∞.
$\pi \int \limits_1^a (1/x-0,1)^2 \, dx$ där $a \to ∞$
Leez
Jag undrar också om ni möjligtvis har lektioner på implicit och explicit derivering?
Simon Rybrand (Moderator)
Hej, nej tyvärr så har vi i nuläget ingenting kring det området.
Leez
Hej!
Jag undrar hur du fick fram 8pi/3 ? För jag får fram att det blir 4pi/3!
Tack! 🙂
Simon Rybrand (Moderator)
Hej, jag ställer upp integralen enligt:
$ 2\pi \int\limits_0^2 (2x^2-x^3) dx = $
$ 2\pi \left[ \frac{2x^3}{3} -\frac{x^4}{4} \right]_0^2 = $
$ 2\pi (\frac{16}{3} – 4) = 2\pi(\frac{4}{3}) = \frac{8\pi}{3} $
Endast Premium-användare kan kommentera.