
Start / Derivata
Derivata
Allt om derivata
Med hjälp av derivata kan du beskriva hastigheten på en förändring vid en viss tidpunkt. Derivatan i en punkt är detsamma som en tangents lutning i en punkt på funktionens graf.
Våra lektioner om derivata
Här hittar du alla lektioner hos oss som handlar om derivata.
Extrempunkter, extremvärden och största och minsta värde Videolektion
Matematik 3c, Matematik 3bLinjär approximation Gratis Videolektion
Matematik 5Genomsnittlig förändringshastighet och ändringskvoter Videolektion
Matematik 3c, Matematik 3b, Matematik 3Tangent och Sekant Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Gränsvärden Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Gränsvärden och förberedelse inför Derivata Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Derivata – Vad är det? Gratis Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Derivatans Definition Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Exempel derivatans definition Videolektion
Matematik 3c, Matematik 3b, Matematik 3Deriveringsregler Gratis Videolektion
Matematik 4Tangentens ekvation och lutning Videolektion
Matematik 3c, Matematik 3b, Matematik 3Deriveringsregler Polynomfunktioner Gratis Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Deriveringsregler Potensfunktioner Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Deriveringsregler Exponentialfunktioner Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Kvotregeln Videolektion
Matematik 5, Matematik 4Produktregeln Videolektion
Matematik 5, Matematik 4Kedjeregeln Videolektion
Matematik 5, Matematik 4Andraderivata Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 4, Matematik 3Växande och avtagande funktioner Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Derivatans nollställen och teckentabell Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Minsta och Största värde Videolektion
Matematik 3c med Avancera I, Matematik 3Derivatans graf och Funktionens graf Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Förändringshastigheter och Derivata – Kedjeregeln Videolektion
Matematik 5, Matematik 4Träna mer på Förändringshastigheter och Derivata – Kedjeregeln Videolektion
Matematik 5, Matematik 4Asymptoter Videolektion
Matematik 4Asymptoter – Problemlösning Videolektion
Matematik 4Mer om derivata
Med hjälp av derivata kan du beskriva förändringshastigheten vid en tidpunkt. Exempelvis kan du tänka dig att en funktion beskriver en bils sträcka. Derivatan av denna funktion beskriver då förändringen av sträckan vid en viss tidpunkt. Därför beskriver då derivatan av funktionen bilens hastighet.
Här nedan kan du läsa en sammanfattning av vad du behöver kunna om derivata på gymnasiet. Framförallt lyfter vi fram de viktigaste begreppen som du lär dig i Matematik 3, 4 och 5.
Gränsvärden och derivatans definition
När du lär dig förstå innebörden av derivata så behöver du börja med gränsvärden och genomsnittlig förändringshastighet. Det beror på att dessa två begrepp är två grundstenar när du lär dig derivatans definition. Derivatans definition ser ut på följande vis:
$f'(x)=$ $\lim\limits_{h \to 0}$ $\frac{f(x+h)-f(x)}{h}$
Derivatans definition används sedan för att ta fram deriveringsregler för olika typer av funktioner. Därför är det bra om du minst har grundläggande förstålse för hur definitionen fungerar.
De viktiga deriveringsreglerna
Deriveringsregler förenklar sättet som du tar fram derivatan av olika funktionstyper. Exempelvis finns det färdiga deriveringsregler för polynomfunktioner, potensfunktioner och exponentialfunktioner. Framförallt börjar du att lära dig dessa regler i kurserna Matematik 3b och c. Sedan fördjupas deriveringsreglerna from kursen Matematik 4 (se nedan).
Derivata och tangentens lutning
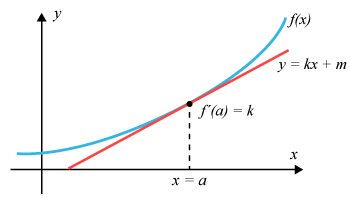
Derivatans värde för en funktion är detsamma som tangentens lutning i en punkt. Därför är denna kunskap viktigt att känna till då den hjälper dig att lösa uppgifter grafiskt eller bestämma ekvationen till tangenten.
Derivatan och grafen
Derivata används även till att beskriva hur funktioner förändras. Därför kan du ta reda på när funktioner växer eller avtar med derivata. Dessutom kan du förstå när en funktion har en maximipunkt eller en minimipunkt. Exempelvis använder du det när du löser optimeringsproblem.
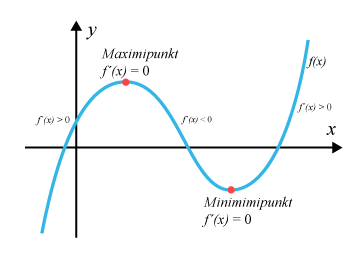
Det kan även vara viktigt att du förstår innebörden av andraderivata. Det beror på att med hjälp av andraderivata kan du se om en punkt på funktionens graf är en minimipunkt eller maximipunkt.
Fördjupning av deriveringsregler
I kursen Matematik 4 får du lära dig fler typer av deriveringsregler. Exempelvis lär du dig att derivera sammansatta funktioner med kedjeregeln och produkter av funktioner med produktregeln. Dessutom lär du dig att derivera kvoter av funktioner med kvotregeln.
Alla dessa regler bygger vidare på grundläggande förståelse av derivatans definition och de första deriveringsreglerna.
Derivata och förändringshastigheter
I matematik 4 fördjupar du dig även i tillämpningar som vi beskriver med sammansatta funktioner. I vissa verkliga skeenden beror en sak på en annan som kan ha en inre funktion. Dessa typer av skeenden benämns som förändringshastigheter och derivata. Exempelvis kan en kubs sida växa med tiden. Kubens volym beror på sidan som i sin tur beror på tiden. Därför har sidan en inre funktion som deriveras med kedjeregeln.
Tolka grafer med asymptoter
En asymptot är en rät linje som grafen till en funktion närmar sig. Du delar upp asymptoter i lodräta, horisontella och sneda asymptoter. Med hjälp av asymptoter och derivata kan du tolka och förstå hur grafer beter sig. Exempelvis kan det röra sig om grafer som inte är definierade för alla x. Därför kan dessa grafer vara lite svårare att snabbt skissa ut för hand.
Höj dina resultat i matematikkursen!
- Högstadiet och hela gymnasiet.
- Mer än 600 supertydliga videos.
- Träna inför ditt nationella prov.
- Dessutom Fysik 1, programmering och högskoleprovet.
Nyheter
Populära kurser
Åk 9
66 lektioner

Matematik 2b
92 lektioner

Matematik 3c
67 lektioner

Högskoleprovet
71 lektioner

Matematik basår
95 lektioner

Fysik 1
92 lektioner
Våra användare gillar oss!
Populära lektioner
Räta linjens ekvation Gratis
Matematik 2
Ekvationslösning
Matematik 1
Vad är Algebra?
Matematik 1
Beteckningen f(x)
Matematik 1
Ohms lag Gratis
Fysik 1
Förenkla algebraiska uttryck
Matematik 1
Tallinjen Gratis
Matematik 1
Vad är funktioner
Matematik 1
Kort division - dividera med uppställning
Matematik högstadiet
Enhetscirkeln Gratis
Matematik 3
Få tillgång till allt för
endast 99 kr/mån
Över 600 lektioner. Ingen bindningstid. Avsluta när du vill.
Köp Premium Prova gratis
