Författare: Simon Rybrand
Simon Rybrand  Anna Karp
Anna Karp
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Linjär approximation
Ibland kan det vara svårt att bestämma värdet för en funktion då denna kan vara komplicerad eller att man inte har tillgång till en räknare. Då kan man bestämma ett ungefärligt funktionsvärde med hjälp av linjär approximation.
Idén här är att man bestämmer ekvationen för en tangent med hjälp av bland annat derivata och sedan bestämmer ett närmevärde med hjälp av tangenten till det sökta funktionsvärdet.
Härledning av tangentens ekvation
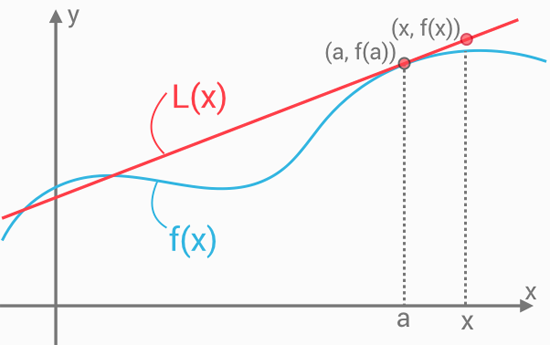
I figuren ovan är en tangent L(x) till funktionen f(x) utritad i punkten (a,f(a)). Denna tangent kan bestämmas på formen y=kx+m. Här vill vi skriva tangentens ekvation allmänt men också på ett vis som gör det enkelt för oss att bestämma närmevärden med hjälp av denna. Vi kommer därför att skriva om tangentens ekvation på slutet så att denna blir enklare att använda senare.
Här gäller att y=f(a), x=a och k=f′(a). Vi söker nu m – värdet:
f(a)=f′(a)⋅a+m⇔
m= f(a)–f′(a)⋅a
Vi kan nu skriva L(x) = kx+m som
L(x)=f′(a)⋅x+f(a)–f′(a)⋅a=
f(a)+f′(a)(x−a)
En tangent L(x) i punkten (a, f(a))(a, ƒ (a)) till en funktion f(x) kan allmänt skrivas som
L(x)=f(a)+f′(a)(x−a)
Exempel på linjär approximation
Vi kan nu använda oss av tangentens ekvation på allmän form form att kunna bestämma närmevärden för funktionsvärden. Viktigt att känna till här är att vi får mindre eller större fel när vi gör denna approximation.
Exempel 1a
Bestäm en linjär approximation till f(x)=x8 kring x=2. Bestäm sedan ett närmevärde till f(2,01) med hjälp av approximationen och beräkna felet som uppstår med en räknare.
Lösning
En tangent L(x) i punkten (a, f(a))(a, ƒ (a)) till en funktion f(x) kan allmänt skrivas som
L(x)=f(a)+f′(a)(x−a)
Vi börjar med att bestämma punkten.
f(2)=28=4 ger tangeringspunkten (2,4)(2,4)
Vi tar nu fram derivatan till funktionen för att kunna sätta in in tangentens ekvation.
f′(x)=−x28
Sen beräknar vi derivatans värde för x=2x=2 vilket är tangeringspunktens xx -värde.
f′(2)=−48=−2
Vi bestämmer nu vår tangents ekvation med värdena ovan och får att
L(x)=4+(−2)(x−2)=4–2(x−2)
Vi beräknar nu närmevärdet till f(2,01) genom att sätta in x=2,01x=2,01 i tangenterna ekvation.
f(2,01)=4−2(2,01−2)= 4−2⋅0,01=4−0,02=3,98
Om vi beräknar f(2,01) med räknare ges svaret f(2,01)≈3,9800995
Felet blir därmed differensen mellan dessa värde, alltså ungefärligt 3,9800995−3,98=0,0000995
Ett väldigt litet fel, vilket visar att linjära approximation kan vara en bra metod för att bestämma närmevärdet till vissa funktioner.
Linjär approximation med GeoGebra
Genom att använda GeoGebra kan du snabbt göra en linjära approximation. Det kan du ta nytta av och använda som stöd till dina manuella beräkningar.
Vi gör samma exempel en gång till med hjälp av Geogbra.
Exempel 1b
Bestäm en linjär approximation till f(x)=x8 kring x=2. Bestäm sedan ett närmevärde till f(2,01) med hjälp av approximationen och beräkna felet som uppstår med en räknare.
Lösning
För att GeoGebra ska ta fram en tangents ekvation behöver du en funktion och en punkt på funktionen. Vi börjar med att skapa dessa.
Skriv in funktionen f(x)=ƒ (x)= x88x i inmatningsfältet och tryck sedan enter. Grafen ritar upp.
Sedan skriver vi f(2)ƒ (2) i nästa inmatningsfält för att beräkna yy -koordinaten tillhörande x=2x=2 och trycker enter för att sedan skriva in punkten (2, 4)(2, 4) i ännu ett nytt inmatningsfält. Självklart kan du beräkna punktens koordinater för hand i stället om du vill. Men alla funktionsvärden är inte lika lätta att beräkna.
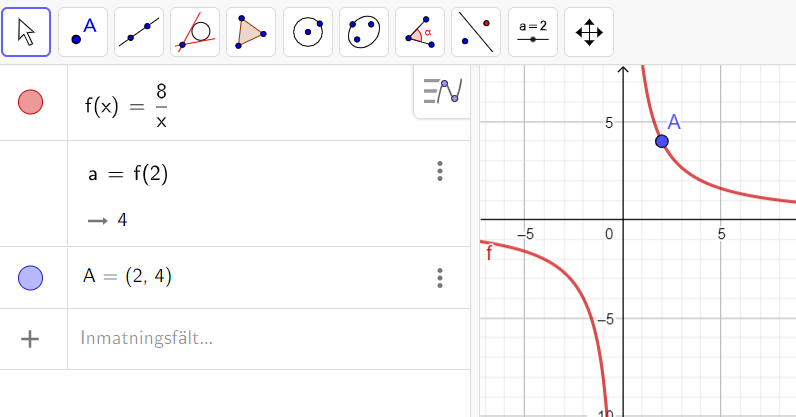
GeoGebra ritar så här långt grafen till funktionen fƒ och punkten (2, 4)(2, 4) som den här kallar AA.
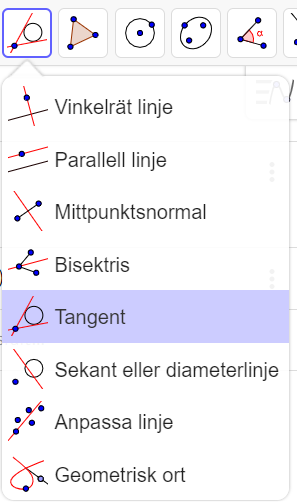
Nu klickar vi på ikonen![]() och väljer Tangent i menyn som kommer upp.
och väljer Tangent i menyn som kommer upp.
Du skapar sedan en tangent i punkten(2, 4)(2, 4) genom att klicka på först punkten och sedan funktionen, eller tvärt om.
Då ritar GeoGebra ut tangenten och anger dess ekvation. Genom att högerklicka i inmatningsfältet kan du välja på vilken form du vill ha tangentens ekvation.
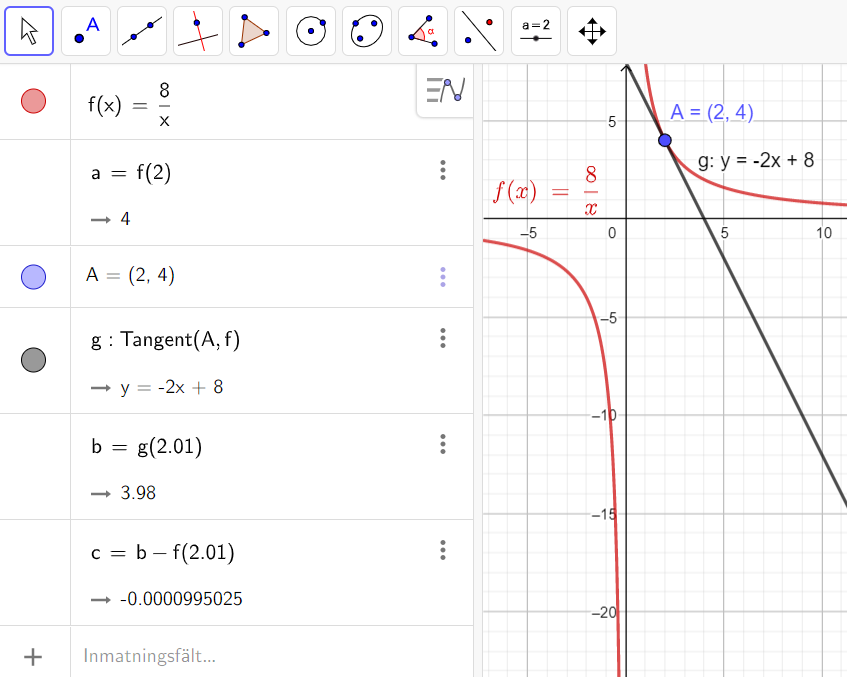
Genom att sedan be GeoGebra att beräkna funktionsvärdet för tangentens ekvation då x=2,01x=2,01 för vi den linjära approximationen. Sist beräknar vi differensen mellan det faktiska värdet och den linjära approximationen. Om du får värdet noll är det för att du har för få värde siffror. Gå då in under inställningar och ändra till fler.
GeoGebra väljer ofta att ”namnge” de olika beräkningarna och funktionerna. Du kan själv välja om du vill använda de namn som GeoGebra sett ditt uttryck eller om du skriver om det igen. Men snabbas är att använda de nya ”namnen”.
Kommer du inte ihåg hur du gör olika inställningar och ändrar formen för funktionsuttryck mm så återvänd till lektionen GeoGebra och Funktioner och GeoGebra och Räta linjens ekvation för att repetera grunderna.
Exempel i videon
- Använda att 4=2 och funktionen f(x)=x för att bestämma ett närmevärde till 5. Bestäm också felet vi får med hjälp av räknare.
- Bestäm utan räknare ett närmevärde till f(0,04) om f(x)=e4x och sedan f(0,04) med en räknare och ange felet.
Kommentarer
e-uppgifter (4)
1.
(2/0/0)E C A B P 2 PL M R K Bestäm tangentens ekvation i x=2 då f(x)=3x2
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
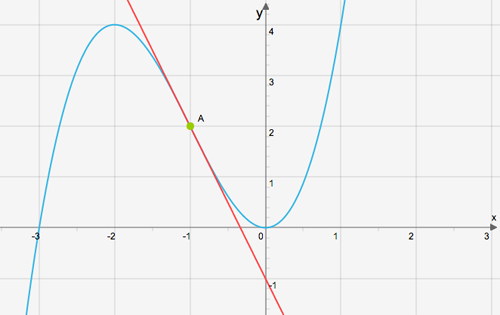
(2/0/0)E C A B P 2 PL M R K I figuren är en tangent utritad som tangerar f(x)=x3+3x2 i punkten A. Bestäm tangentens ekvation på formen y=kx+m.
 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(2/0/0)E C A B P PL 2 M R K Använd att 9=3√9=3 och funktionen f(x)=xƒ (x)=√x och bestäm ett närmevärde med fyra decimaler till 8√8 med hjälp av linjär approximation.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B P 1 PL M R K Använd svaret du fick från fråga 3 och en räknare för att bestämma felet med fyra decimaler.
Beräkna 8 med hjälp av en räknare och jämför med svaret på den linjära approximationen.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (2)
5. Premium
(0/2/0)E C A B P PL 2 M R K Bestäm en linjär approximation till f(x)=e2x⋅sin(x) kring x=0 och använd denna till att beräkna f(0,02) utan räknare.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(0/2/0)E C A B P PL 2 M R K Låt f(x)=2x⋅ln(x)ƒ (x)=√x·ln(x)2 . Bestäm ett närmevärde till f(1,2)ƒ (1,2) med hjälp av linjär approximation kring punkten x=1x=1. Ange felet med fem decimaler i textrutan nedan.
Svar:Ditt svar:Rätt svar: 0,00014(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (1)
7. Premium
(0/0/2)E C A B P PL 2 M R K Ekvationen 4⋅sin(2x)+x=e3x−x4·sin(x2 )+x=√ex3 −x har en lösning nära x=0x=0. Bestäm ett närmevärde till lösningen med hjälp av linjär approximation.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Adane Hailu
Hej!
Fråga nummer 7.
Varför subtraherar vi från närmevärde den exakta värden, alltså för att få felet måste vi subtraherar från exakt värden eller? Tack!
Simon Rybrand (Moderator)
Det du vill ha är differensen mellan det exakta värdet och närmevärdet. För att få det så är det enklaste att ta det största av de två och subtrahera med det andra.
Då får du ett positivt svar och därmed skillnaden mellan dem.
Janne
Ni har ett räkne fel vid tiden 08:29 inom parantesen 4(x-4) där skall väl stå 4(x-0)??
Simon Rybrand (Moderator)
Hej
Ja, a=0 så det står fel där i videon. Vi har korrigerat videon nu.
Tack för att du sade till om detta!
Endast Premium-användare kan kommentera.