Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik Nivå 2
/ Linjära funktioner
Substitutionsmetoden
Substitutionsmetoden är, tillsammans med additionsmetoden, en algebraisk metod för att lösa linjära ekvationssystem.
Att substituera betyder att vi ”byter ut” eller ”ersätter” något. Med substitutionsmetoden ersätter vi variabler med uttryck eller värden för att lösa ekvationssystemet.
Substitutionsmetoden går ut på att först lösa ut en variabel i en av ekvationerna. Det uttrycket sätter vi sedan in i den andra ekvationen. Då får vi en ekvation med bara en variabel, som vi kan lösa.
När vi har fått värdet på den första variabeln sätter vi in det i någon av ekvationerna för att ta reda på den andra variabelns värde.
Det går också att lösa linjära ekvationssystem grafiskt, men då får vi inte helt säkert exakta värden utan ungefärliga (approximativa) lösningar. I denna kurs behöver du kunna lösa ekvationssystem både algebraiskt och grafiskt.
Så använder vi substitutionsmetoden
Principen är alltså att kunna ersätta, eller med andra ord substituera, en eller flera variabler i ekvationssystemet mot ett uttryck från en annan ekvation i systemet. På så sätt får vi till slut en ekvation med endast en variabel, som då blir lösbar. Därefter kan vi även ta reda på den andra variabelns värde.
I denna kurs börjar vi med ekvationer med två okända. För att lösa dessa måste vi ha två olika samband mellan de okända.
Med substitutionsmetoden gör vi följande steg för att hitta lösningen:
Substitutionsmetoden
- Lös ut en variabel från en av ekvationerna.
- Substituera (ersätt) variabeln i den andra ekvationen med uttrycket som vi har tagit fram. Nu har vi endast en okänd variabel i ekvationen.
- Lös ekvationen.
- Ersätt variabeln med värdet vi just bestämt för att även bestämma den andra variabelns värde.
Tips:
Om en variabel i någon av ekvationerna redan står ensam, välj den variabeln — det sparar lite arbete!
Nu tittar vi på några räkneexempel.
Exempel 1
Lös ekvationssystemet
$\begin{cases} y-x=2 \quad (1) \\ 3=6x-y \quad (2) \end{cases}$
Lösning
Vi löser ut $y$y från ekvation (1)
$y-x=2$y−x=2 addera båda leden med $x$x
$y=x+2$y=x+2
Nu kan vi ersätta $y$y i ekvation (2) med $x+2$x+2. Det vill säga, vi gör en substitution så att vi bara har en variabel, $x$x, istället för två, $x$x och $y$y, i den ekvationen.
$3=6x-(x+2)$3=6x−(x+2) förenkla HL
$3=6x-x-2$3=6x−x−2
$3=5x-2$3=5x−2 addera båda leden med $2$2
$5=5x$5=5x dividera båda leden med $5$5
$x=1$x=1
Vi beräknar nu $y$y för värdet $x=1$x=1 genom att ersätta $x$x med $1$1 i ekvation (1).
$y-1=2$y−1=2 addera båda leden med $1$1
$y=3$y=3
Nu har vi lösningen till ekvationssystemet, det vill säga $x$x-värdet och $y$y-värdet som gör att likheten gäller i både ekvation (1) och (2) samtidigt.
$\begin{cases} x=1 \\ y=3 \end{cases}$
Lägg märke till att lösningen till ett ekvationssystem inte anges som koordinaterna för en punkt, utan på formen $\begin{cases} x=a \\ y=b \end{cases}$ eller $x=a$x=a och $y=b$y=b.
Exempel 2
De två linjerna $2y-2x=2$2y−2x=2 och $3y+6x=21$3y+6x=21 skapar en triangel tillsammans med $y$y-axeln. Bestäm de exakta koordinaterna för triangelns hörn.
Lösning
Den här uppgiften kan vi lösa genom att göra följande.
- Använda substitutionsmetoden för att bestämma linjernas skärningspunkt med varandra.
- Skriva om ekvationerna till formen $y=kx+m$y=kx+m. Då får vi linjernas skärningspunkt med $y$y-axeln genom $m$m-värdet.
Vi löser först ekvationssystemet
$\begin{cases} 2y-2x=2 \quad (1)\\ 3y+6x=21 \quad (2) \end{cases}$
Vi börjar med att lösa ut $y$y ur ekvation (1)
$2y-2x=2$2y−2x=2 dividera alla termer med $2$2
$y-x=1$y−x=1 addera båda leden med $x$x
$y=x+1$y=x+1
Nu byter vi ut $y$y i ekvation (2) mot $x+1$x+1 och får ekvationen
$3\left(x+1\right)+6x=21$3(x+1)+6x=21 förenkla VL
$9x+3=21$9x+3=21 subtrahera båda leden med $3$3
$9x=18$9x=18 dividera båda leden med $9$9
$x=2$x=2
Nu har vi $x=2$x=2 och kan sätta in detta värde i ekvation (1) för att bestämma $y$y.
$y=x+1=2+1=3$y=x+1=2+1=3
Linjerna skär alltså varandra i $x=2$x=2 och $y=3$y=3 vilket ger oss ett av triangelns hörn $\left(2,\text{ }3\right)$(2, 3).
Nu går vi vidare och skriver om båda ekvationerna på formen $y=kx+m$y=kx+m.
Ekvation (1)
Denna ekvation har vi redan skrivit om till $y=x+1$y=x+1.
Linjen skär $y$y-axeln där $y=1$y=1 och $x=0$x=0 vilket ger oss hörnet $\left(0,\text{ }1\right)$(0, 1).
Ekvation (2)
$3y+6x=21$3y+6x=21 dividera båda leden med $3$3
$y+2x=7$y+2x=7 subtrahera båda leden med $2x$2x
$y=-2x+7$y=−2x+7
Linjen skär $y$y-axeln där $y=7$y=7 och $x=0$x=0 vilket ger oss hörnet $\left(0,\text{ }7\right)$(0, 7)
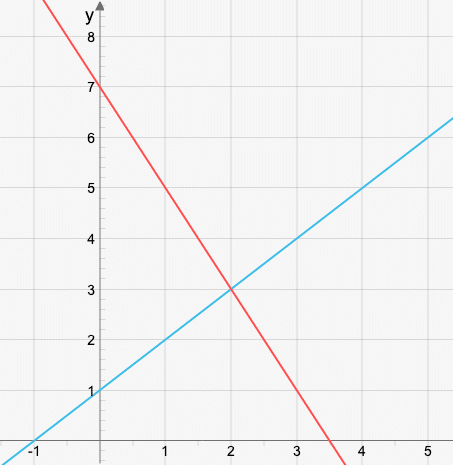
Nu har vi alla koordinater för triangelns hörn, dessa är
$\left(2,3\right)$(2,3), $\left(0,1\right)$(0,1) och $\left(0,7\right)$(0,7).
Om vi använder en räknare eller datorn för att rita ut linjerna ser det ut på följande vis.
Exempel i videon
- Lös $\begin{cases} x-2=y \quad (1)\\ y+x=4 \quad (2) \end{cases}$ med substitutionsmetoden.
- Lös $\begin{cases} 4x+2y=10 \quad (1)\\ 3y-6x=3 \quad (2) \end{cases}$ med substitutionsmetoden.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (7)
-
1. Premium
Lös följande ekvationssystem med substitutionsmetoden.
$\begin{cases} y=2x+3 \\ y=3x-4 \end{cases}$
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
Lös följande ekvationssystem med substitutionsmetoden.
$\begin{cases} x+y=5 \\ x+1=y \end{cases}$
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: ekvationssystem Linjära ekvationssystem Linjära funktioner substitutionsmetodenRättar... -
3. Premium
Lös följande ekvationssystem med substitutionsmetoden.
$\begin{cases} x+3y=-3 \\ 2x-y=8 \end{cases}$
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: ekvationssystem Linjära ekvationssystem Linjära funktioner substitutionsmetodenRättar... -
4. Premium
Lös ekvationssystemet $\begin{cases} 2x + 2y = 4 \\ 3x – 2y = 1 \end{cases}$
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
5. Premium
Bestäm talet $a$a i ekvationen $3x+2y=a$3x+2y=a så att uttrycket $3x+2y-4$3x+2y−4 får värdet $8$8.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
6. Premium
Lös ekvationssystemet $\begin{cases} 2x+3y=8 \\ 4x+y=-4 \end{cases}$.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
7. Premium
Bestäm koordinaterna för skärningspunkten mellan linjerna $y=2x-8$y=2x−8 och $x+y=10$x+y=10 med hjälp av substitutionsmetoden.
Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: SubstitutionsmetodenLiknande uppgifter: koordinatsystem Linjära ekvationssystem Linjära funktioner skärningspunkt substitutionsmetodenRättar...c-uppgifter (3)
-
8. Premium
Lös det linjära ekvationssystemet $\begin{cases} y+x=-1 \\ 2y+14=4x \end{cases}$
Svar:Ledtråd
Ledtråd 2
Ditt svar:Rätt svar:💡 Enheten saknas i ditt svarBedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: additionsmetoden Algebra grafisk lösning Linjära ekvationssystem Linjära funktioner substitutionsmetodenRättar... -
-
9. Premium
Bestäm värdena för $a$a och $b$b så att ekvationssystemet $\begin{cases} x+ay=5 \\ 2bx + y =a+1 \end{cases}$ får lösningen $\begin{cases} x=1 \\ y=2 \end{cases}$.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
10. Premium
Lös ekvationssystemet algebraiskt
$\begin{cases}(x-4)(y+3)=x(y-5)+4(y+1)\\ 4(y-1)+x=2(x+y) \end{cases}$
Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra ekvationssystem Funktioner linjära ekvationer Linjära ekvationssystem substitutionsmetodenRättar... -
-
Uppgiften är en del av en abc-fråga. Vad vill du göra?
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
Yasin
Förklaringen på uppgift 8 ska vara algebraisk. Ni har råkat lösa den geografiskt.
Eddler
Hej!
Du har rätt, förklaringen använde en grafisk metod. Vi har nu lagt till en algebraisk lösning också, så du kan välja den metod som passar dig bäst.
Hör av dig om du har fler frågor!
Josefin E
Kan ha fel, men tror det är någonting fel med fråga 9.
Någonstans blir y som är 2 plötsligt en 1 i uträkningen när man trycker på förklaring 🙂
Eddler
Hej Josefin!
$y = 2$ är korrekt substituerat genom hela lösningen. I andra ekvationen sätts $y = 2$ in och vi får $2b + 2 = a + 1$. Sedan subtraherar man $1$ från båda leden: $2b + 2 – 1 = a + 1 – 1$, det vill säga $2b + 1 = a$. Ettan som dyker upp är alltså inte $y = 1$, utan ett resultat av algebran (eftersom $2 – 1 = 1$). Hör av dig om du har fler frågor!
Lennie Skånberg
Hej!
I exempel 2 i videon så räknar du ut att X=1 för att sedan skriva att vi ska sätta in X=3 i (1)
Stämmer verkligen det?
Du säger även att vi ska byta ut X mot 3 när vi ska lösa (1) men i talet står det -2x*1
gabrielle herendi
Vet ej hur man räknar ut detta;
y=4
2x+y=8
Ercan Durak
Hej simon, behöver hjälp med en uppgift:
0.8x+2.5y=39
2x+3.4y=86
Tack för svar!:D
Nadja Furberg
3x+2y=1
X-2=3
Hur löser jag detta enligt subtitutionsmetoden
Johnny Johansson
Hej!
Jag har problem med en fråga i exponent 2b boken!
Hur löser jag detta?
8,3x+5,9y=300
x+y=45
Jag löste ut y först så att y=45-x
Satte sedan in det i den första ekvationen
8,3x+5,9(45-x)=300 –> Multiplicerade in 5,9
8,3x+265,5-5,9x=300 –> Lägger ihop x
14,2x+265,5=300 –> Flyttar över 265,5
14,2x=300-265,5
14,2x=34,5 –> Delar med 14,2
x=2,429
Jag vet att jag gör fel nån stans men vart?
Johnny Johansson
Kanske ska tillägga vad frågan var!
Peter kör ett 45 minuter långt träningspass i ett gym med dels en roddmaskin och dels en spinningcykel.
När han använder roddmaskinen förbrukar han 8,3kcal/min och med spinningcykeln 5,9kcal/min.
Han vill totalt förbränna 300 kcal under sitt träningspass.
a) Inför lämpliga variabler och ställ upp ett ekvationssystem som kan användas för att beräkna hur lång tid Peter bör träna vid varje maskin.
b) Hur lång tid ska han tillbringa vid varje maskin?
Berkan991
Ekvationen 2x-2y=4
3x-2y=1
spelar det roll vilken man ändrar till k-form? jag valde den längst uppe för den är lättast!
2y=4-2x
tar in 4-2x i andra ekvationen… 3x-2(4-2x)
Men här har ni istället gjort 3x-(4-2x)….. vart är 2an?
Och hur fick ni till y=1
Alexander Giang
Tjena! Undrade hur jag löser:
(1) 2x+2y=4
(2) 3x-2y=1
Vet inte hur jag ska göra när jag får mer än 1y och 1x på båda sidorna. :c
Alexander Giang
Jadå! Tack så mycket!
RedEagle
Hej,
ett litet misstag har skett i texten, det står ”LÖSNING AV EKVATIONSSYSTEM MED ADDITIONSMETODEN” men det ska stå väl stå substitutionsmetoden?
jonasfredriksson89@gmail.com
X + 2Y = 23
X gånger y = 65
Hur använder jag Ersättningsmetoden här?
Simon Rydvall
Om jag har ett tal där det står följande, Lös följande ekvationssytem med valfri algebraisk metod.
då har man :
3x+2y=9
-x+3y=8
Hur kan jag räkna ut detta tal på enklaste sätt?
Zandra Hedman
jag ska liksom lösa ekvationen här exakt. Och ge ett närmvärde. Men jag vet inte hur jag ska kunna få flera decimaler.
Talet är 10 upphöjt till x =250. Ska jag lösa ut vad x står för? men hur ska jag kunna få decimaler på de?
Zandra Hedman
Hejjag får inte ihop det hur jag ska lösa talet
3x+4y=-1
3x+2y=1
Detta ska lösas med den valfria metoden. För om jag fattar det rätt är tanken att man ska räkna ut talet för att de att dom betyder samma. Och jag vet inte hur jag ska lösa det. Kan ju inte dividera den med 2 osv. Så skulle gärna vilja ha förklarat hur jag löser den. Tack så länge
Fredric Hallgren
Hej Jag har ett tal som jag bara inte kan lösa.
För vilket värde på a saknar ekvationssystemet nedan lösning?
ax+2y=6
9x+3y=12
Hur fasen skall jag kunna få fram A?
Caroline lundin
hej ! hur löser man :
1.
2X+3Y=8
4x+y=-4
2.
x-5y=-3
4x-3y=5
Med Sub. metoden, jag sitter fast ! tack !
Mattias
Hur fasen listar man ut {y=2x+3 Det är ju två ”y=” ??
{y=3x−4
Stefan Lindblom
Hej Simon
Hur vet man när man ska använda additionsmetoden, samt substitutionsmetoden, eller funkar båda bra till alla?
Mvh
nattr1
Hej,
hur kan jag lösa ett ekvationssystem grafiskt om
y=x
y=9-2x
jag har det svårt med y=x….
Mvh
Natasa
Maria
Hej!!
Skulle du kunna förklara hur man löser ut en sådan ekvation 2y=3x med en Texas-82 miniräknare??
Tack på förhand!
mimmipalmgren
Hej!
Skulle jag kunna få hjälp med att lösa detta ekvationssystem
Y=2x+1
3x+2y=21
Tack!!
EllinorE
Hej, hur ska jag lösa
y=3x
y=3x+4
med substitutionsmetoden?
annelie.b
Hej Simon,
Skulle du använda substitutionsmetoden för att lösa den här uppgiften eller något annat sätt? Får inte ihop det det om jag använder substitutionsmetoden.
9. Vilka två linjer skär varandra i en punkt där både x-koordinaten och y-koordinaten är negativa?
A y = –x + 4 och y = x
B y = x + 4 och y = –x
C y = x – 4 och y = –x
D y = –x – 4 och y = x
(Rätt svar: D)
Tack på förhand!
/Annnelie
annelie.b
Tack!! 🙂
johana_lahti
Hej. Jag förstå inte, när jag använder substitutions metoden hur vet jag då vilken av ekvationerna jag ska byta ut med?
johana_lahti
Jag förstår hur själva substitutions metoden går till, men sen när jag ska använda mig av metoden förstår jag inte hur jag ska börja och väldigt svårt med att använda mig av den. Hur ska jag tänka? Hur vet jag hur man börjar? Förstår allt när ni visar i videon men inte när jag får ett tal.
annelie.b
Hej, hur kommer det sig att du i exempel 2 på videon kan byta tecken på -x=5 till x= -5? Vad är det för regel eller sätt att tänka som man använder där? När kan/ ska man i andra fall tänka så?
Tack på förhand,
Annelie
annelie.b
PS det vore bra och användarvänligt om ni la till en funktion som gör att man får ett mail med en notis när någon har svarat på en kommentar som man har skrivit, istället för att man ska gå in och hålla koll efter svar. /Annelie
nti_ma2
Hej kan du hjälpa mig med denna?
Y=3x-4
Y=x+4
Mvh Patrik
nti_ma2
tack som fasen, detta kan ha räddat min helg som kommer behöva spenderas i mattens tecken;)
nti_ma2
hej
hur blir när en av ekvationen har inte variabeln x .
y= x+2
Y= 5
mvh
eli
annab87
Hej, tycker att dessa metoder att lösa detta på är extremt krångliga. Finns det inga olika mönster eller tips man kan ta till vara på när man vill lösa dessa?
mvh
friflygare
Hej, har lite strul med ett tal i boken som jag inte riktigt får att gå ihop. För vilka värden på a saknar ekvationen 45ax – 27 = 3×2 reella rötter?
friflygare
Ja du har rätt. Såg att när jag kopiera in så blev det lite fel. Ska alltså vara.
45ax – 27 = 3x^2
Miguel
Jag har ett problem med vissa ekvationer då jag ska använda mig av substititionsmetoden.
Om jag ska lösa följande ekvationer;
1:
2x+3y=8
4x+y=-4
Ska jag lösa ut Y på denna? Jag finner det lite krångligt när sådana ekvationer dyker upp. Jag vet inte riktigt hur jag ska använda mig av metoden.
2:
x-5y=-3
4x-3y=5
Samma här. Vad jag vill veta är hur jag ska angripa ett sådant problem så jag kan lösa dessa.
Tack på förhand!
Miguel
Så enkelt och logiskt när du lägger fram det så! Tusen tack!
liridona_m@hotmail.com
Hej. Hur löser man denna ekvationen
y=2x+3
3y=12+3x
och denna
x+y=7
x-y=1
Tacksam för svar.
liridona_m@hotmail.com
Hej vad blir
5x+y-2=0
2x-y-3=0
och hur räknar man ut det?
MVH
Miguel
förstod inte riktigt hur du fick -x= 5 och sen x= -5.
När jag räknade ut det fick jag 2x+5?! Vart gjorde jag fel?
Moa Nordin
Tänker jag fel om jag tänker att 2x+5 inte borde bli x=-5 utan istället -2,5 eftersom att vi borde dividera de båda leden med 2 då det står 2x?
minerva
detta är då en fråga som jag hoppade över och vill nu försöka lösa men förstår bara inte. ”Multiplicera in och lös sedan ut y”
y – 7 = -3(x-2)
michaela
(1) x-2y=4
(2) 2x+2y=2
x=2
y=-1
Korrekt, eller har jag helt missuppfattat?
michaela
Tack för tipset, det ska jag göra!
EvaStenmark
hej!
hur löser man:
x+3y=1
3x+2y=-11
jj
x + 3y = 96
x + y + 2z= 126
2x + 2y +z = 159
shirali110
Hej !
Hur vi kan lösa den här ekvationen :
y=4x
5x-2y-3=0
?
Tack för svaret om detta linjära ekvationssystem
Endast Premium-användare kan kommentera.