Name: Blandade övningar - Statistik - (Matte 2) - Eddler
Brand: Eddler
Rating: 4.21 (14 reviews)

Matematik 2

Mina Kursgrupper
MV Kurser

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

Innehåll

Fördjupning Ma2c
Summatecknet som skrivsätt vid beräkning av medelvärde
Kommentarer

I den här lektionen får du möjlighet att träna på att lösa ett antal vanliga typer av problemställningar som ofta behandlas inom statistiken. Lektionen innehåller ingen video då ingen ny teori presenteras.

Vi repeterar kort de begrepp som är bra att känna till inom statistiken. Återvänd till respektive lektion för att få fördjupande förklaringar och exempel på respektive begrepp.

Medelvärde

$\text{Medelvärdet}=$Medelvärdet= $\frac{\text{Summan alla värden}}{\text{Antalet värden}}$Summan alla värdenAntalet värden

Median
Mittenvärdet i en datamängd där talen har ställts upp i storleksordning. Om det är ett ojämnt antal tal blir medianen mittenvärdet. Om det är ett jämnt antal tal blir medianen medelvärdet av de två mittersta talen.

Typvärde
Det värde som förekommer flest antal gånger.

Variationsbredd
Skillnaden mellan det största och det minsta värdet.

Percentil
Värdet där en viss procent av observationerna hamnar nedanför.

Övre Kvartilen
Medianen mellan mittenvärdet och högsta värdet.

Undre/lägre kvartilen
Medianen mellan mittenvärdet och lägsta värdet.

Standardavvikelse
En egenskap hos vissa statistiskt fördelade resultat.

$ \text{Standardavvikelse} = \sqrt{varians} $

$ \text{Varians} =$ $\frac{\text{summan av avvikelserna i kvadrat}}{\text{antal värden}-1}$summan av avvikelserna i kvadratantal värden−1

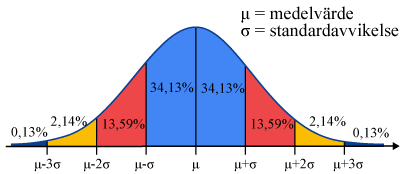
Normalfördelningskurvan

Normalfördelningskurvan kan användas för att beräkna hur stor andel olika resultat fördelas.

Fördjupning Ma2c
Summatecknet som skrivsätt vid beräkning av medelvärde

För att slippa skriva så mycket kan vi använda oss av summatecknet $\Sigma$Σ när vi beräknar medelvärdet. Detta skrivsätt dyker vanligtvis endast upp i Matematik 2c.

[mvdefinitions]

Medelvärde

$\overline{x}=$x= $\frac{x_1+x_2+x_3+…+x_n}{n}$x₁+x₂+x₃+…+x_nn där $\overline{x}$x är medelvärdet av $n$n antal observationer.

Då summan $x_1+x_2+x_3+…+x_n$ x₁+x₂+x₃+…+x_nkan skrivas som $\sum^{^n}_{_{_{k=1}}}x_k$ ∑ⁿ_{_k=1}x_k kan vi även teckna medelvärdet på följande vis.

Lösning

Så medelvärde är $8$ 8. $\frac{\sum_{_{_{k=1}}}^{^{^n}}x_k}{n}$∑_k=1^ⁿx_kn där $\overline{x}$x är medelvärdet av $n$n antal observationer.

Uttrycket i täljaren läses som ”Summa $x_k$ x_k då $k$ k går från $1$ 1 till $n$ n”.

Exempel 2

a) Hur många observationer ingår i datamängden vars medelvärde motsvara likheten $\overline{x}=$x= $\frac{\sum_{_{_{k=1}}}^{^{^7}}\left(2k\right)}{7}$∑_k=1^⁷(2k)7

b) Beräkna medelvärdet $\overline{x}$x

Lösning

a) Vi jämför vårt medelvärde med den ursprungliga formeln.

$\overline{x}=$x= $\frac{\sum_{_{_{k=1}}}^{^{^n}}x_k}{n}$∑_k=1^ⁿx_kn

Eftersom att $n$n är antal observationer ser vi att det är $7$7 stycken observationer.

b) Vi sätter in våra värden och får att då

$\sum_{_{_{k=1}}}^{^{^7}}\left(2k\right)=2\cdot1+2\cdot2+2\cdot3+2\cdot4+2\cdot5+2\cdot6+2\cdot7=56$∑_k=1^⁷(2k)=2·1+2·2+2·3+2·4+2·5+2·6+2·7=56

får vi att medelvärdet $\overline{x}$x är

$\overline{x}=$x= $\frac{\sum_{_{_{k=1}}}^{^{^7}}2k}{n}=\frac{56}{7}=$∑_k=1^⁷2kn =567 = $8$8

Så medelvärde är $8$8.

Regression
Att utgå från ett statistiskt material och anpassa en funktion som beskriver sambandet mellan variablerna.

[/mvdefinitions]

Nästa lektion: Kapiteltest – Statistik Ma2a

Kommentarer

Lisa Rahmani

2016-05-10

Man kan väll visst få medelvärdet om man räknar ut procentandelen för varje ”låda” dvs 25% från minsta värdet till nedre kvartil, 25% mellan nedre kvartil till medianen, 25% från medianen till övre kvartil och 25% från övre kvartil till högsta värdet?

Ex. (frågan om datorspel)

0min-90min spelade 25% av 49 elever.
Detta ger 0.25 * 49 = 12.25, avrundat till 12 pers.

Om jag ska räkna ut medelvärdet ENDAST för denna gruppen (orkar ej göra alla 4 grupper/lådor precis nu!) här tar jag nu alla värden / antalet personer dvs 90/12 = 7.5 min är alltså medelvärdet för gruppen mellan minsta värdet och nedre kvartil.

Eller?

Simon Rybrand (Moderator)

2016-05-13

Låt säga att det är 12 personer inom denna grupp, dvs antalet som spelar 0 – 90 min. Vi vet dock ingenting om dessa personers exakta tider så de kan tex spela 0 minuter allihop eller 80 minuter allihop. Dvs medelvärdet inom gruppen kan variera.

Lisa Rahmani

2016-05-13

Förstår nu! Tack!

Janne

2015-04-24

Fråga tre till denna video borde förtydligas för att Jan-Erik skall få rätt. Detborde väl stå på varandra följande heltal!

Pedro Veenekamp

2015-04-24

Egentligen finns det inga på varandra följande tal om inte heltal. Så snart man använder kommatecken gäller inte längre uttrycket ”på varandra följande tal”. Mellan två heltal finns det nämligen oändliga tal och därför går det inte att hitta två på varandra följande tal om talen inte är heltal. Till exempel: 0,8 och 0,9 är inte på varandra följande tal för att det finns oändliga tal mellan de som till exempel 0,80001 och 0,80002 … men även de är inte på varandra följande tal för att det finns oändliga tal mellan de också: 0,8000100001…
Alltså det går bara att ha på varandra följande tal om de är heltal … finns ingen annan möjlig tolkning.

GenIT

2012-09-29

Problemlösning Statistik funkar inte och i Potenser med rationella exponenter finns det ett räknefel.

Simon Rybrand (Moderator)

2012-09-30

Hej, Vi har fixat denna video så att den fungerar och även lagt till ett interaktivt test på statistik. Vi fixar räknefelet i videon om potenser snarast!

Endast Premium-användare kan kommentera.

Träna mer

E
0/15
C
0/15
A
0/7

Totalpoäng

0/37

e-uppgifter (10)

1.
(2/0/0)
E C A

B 1

P 1

PL

M

R

K

Ett företag tillverkar kattmat på burk där märkningen anger att varje paket skall innehålla $500$ 500 gram. Vikten på burkarna är normalfördelad kring medelvärdet $490$ 490 gram med standardavvikelsen $10$ 10 gram.

Hur många procent av kattmatsburkarna innehåller mindre än $500$ 500 gram?
Svar:

Ditt svar:
Rätt svar: $84\%$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_B Godtagbar ansats tex visar förståelse av att $\mu+\sigma$ motsvarar värden under $500$ gram.
+1 e_P Redovisad lösning med korrekt svar. ( $84\%$ )

Rättad
Rättar...
2.
(1/0/0)
E C A

B

P

PL 1

M

R

K

Armando har tio grisar på sin gård. Det är $4$ 4 galtar (hanar) och dessa väger tillsammans $1080$ 1080 kg. De sex suggorna (honorna) har en medelvikt på $220$ 220 kg.

Vilken är medelvikten på alla tio grisarna?
Svar:

Ditt svar:
Rätt svar: $240$ kg
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_PL Redovisad lösning med korrekt svar. ( $240$ kg)

Rättad
Rättar...
3.
(2/0/0)
E C A

B 1

P

PL

M

R 1

K

Datamängden motsvarar en statistisk undersökning av hur många hål i tänderna en viss population hade.

$0\text{, }0\text{, }0\text{, }0\text{, }0\text{, }1\text{, }1\text{, }1\text{, }1\text{, }1\text{, }1\text{, }1\text{, }2\text{, }2\text{, }2\text{, }2\text{, }2$ 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2.

Vilket läges- eller spridningsmått av alternativen nedan är minst?
- Medelvärdet
- Standardavvikelsen
- Variationsbredden
- Medianen
- Alla värdena är lika stora.
Bedömningsanvisningar/Manuell rättning
- +1 e_B Visar förståelse för minst två av begreppen.
- +1 e_R Godtagbart resonemang med korrekt svar. (Standardavvikelsen)
- Rättad
Rättar...

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

4. Premium
(1/0/0)
E C A

B

P

PL 1

M

R

K

Du köper en godispåse som ska väga $200$ 200 g enligt märkningen på påsen. Din kompis jobbar på företaget som tillverkar godiset och hon berättar att medelvärdet på påsarna faktiskt bara är $195$ 195 g, och att påsarnas vikt är normalfördelade med en standardavvikelse på $8$ 8 g.

Du väger den påse du har köpt och inser att du har tur, du har fått en av de $0,13\%$ 0,13% av påsarna i tillverkningen som väger mest.

Vad väger din påse minst?
Svar:

Ditt svar:
Rätt svar: $219$ gram
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_PL Redovisad lösning med korrekt svar. ( $219$ g)

Rättad
Rättar...
5. Premium
(1/0/0)
E C A

B 1

P

PL

M

R

K

Bestäm standardavvikelsen för följande datamängd.

$4,\text{ }4,\text{ }4,\text{ }8,\text{ }8,\text{ }12,\text{ }15,\text{ }20,\text{ }20,\text{ }20$ 4, 4, 4, 8, 8, 12, 15, 20, 20, 20

Ange svaret med en decimals noggrannhet.
Svar:

Ditt svar:
Rätt svar: $6,9$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_B Redovisad lösning med korrekt svar. ( $6,9$ )

Rättad
Rättar...
6. Premium
(1/0/0)
E C A

B

P

PL 1

M

R

K

Ett företag tillverkar kattmat på burk där märkningen anger att varje paket skall innehålla $500$ 500 gram. Vikten på burkarna är normalfördelad kring medelvärdet $490$ 490 gram med standardavvikelsen $10$ 10 gram.

Kattmatsföretaget har fått kritik och bestämmer sig att minst $84\%$ 84% måste innehålla $500$ 500 gram eller mer kattmat.

Vilket blir det nya medelvärdet om standardavvikelsen fortfarande är $10$ 10 gram?
Svar:

Ditt svar:
Rätt svar: $510$ gram
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_PL Redovisad lösning med korrekt svar. ( $510$ g)

Rättad
Rättar...
7. Premium
(2/0/0)
E C A

B

P

PL 1

M

R 1

K

Jan-Erik påstår att medelvärdet för fem på varandra följande tal alltid är lika med talens median. Olle påstår att detta inte stämmer alls.

Vem har egentligen rätt?

Träna på att motivera ditt svar matematiskt.
- Omöjligt att svara på om vi inte vet vilka värden det rör sig om.
- Jan-Erik har rätt.
- Olle har rätt.
- Ingen av dem.
Bedömningsanvisningar/Manuell rättning
- +1 e_PL Korrekt svar. (Jan-Erik har rätt)
- +1 e_R Godtagbart resonemang.
- Rättad
Rättar...
8. Premium
(2/0/0)
E C A

B

P 1

PL

M 1

R

K

Du frågar din lärare Anita hur lång hon är. Hon berättar att i hennes familj är de fyra personer och medellängden är $174$ 174 cm. Räknar man bort hennes längd så höjs medellängden till $178$ 178 cm.

Hur lång är din lärare?
Svar:

Ditt svar:
Rätt svar: $162$ cm
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_M Tecknar en ekvation som motsvarar medelvärdet på längden i familjen.
+1 e_P Redovisad lösning med korrekt svar. ( $162$ cm )

Rättad
Rättar...
9. Premium
(2/1/0)
E C A

B 2 1

P

PL

M

R

K
M NP

År 1798 försökte engelsmannen Henry Cavendish bestämma jordens densitet. Han gjorde ett antal mätningar och beräknade sedan värden på jordens densitet.

I diagrammet nedan visas 29 av Cavendishs värden på jordens densitet.

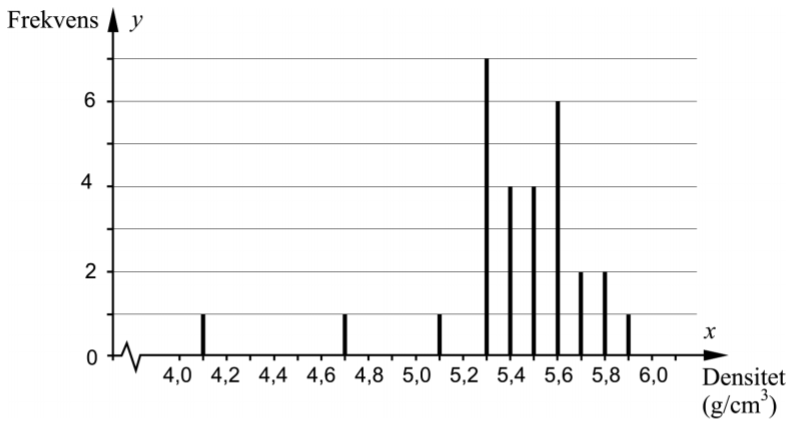
a) Bestäm variationsbredden.

b) Bestäm medianen.

c) Standardavvikelsen för värdena ovan är $0,35$ 0,35 g/cm $^3$ ³.

Ange med ett ord vad som händer med standardavvikelsens storlek om de två lägsta värdena $4,1$ 4,1 och $4,7$ 4,7 plockas bort.
Standardavvikelsen blir…
Svar:

Ditt svar:
Rätt svar: a) $1,8$ g/cm $^3$ b) $5,5$ g/cm $^3$ c) mindre
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 e_B Korrekt svar. ( $1,8$ g/cm $^3$ )
+1 e_B Korrekt svar. ( $5,5$ g/cm $^3$ )
+1 c_B Godtagbart svar (t.ex. mindre)

Rättad
Rättar...
10. Premium
(1/0/0)
E C A

B

P

PL

M

R 1

K

Din kompis har försökt beräkna standardavvikelsen för ett statistiskt material från en stickprovsundersökning och ber dig kontrollräkna för att säkerställa att det blivit rätt. Studera uträkningen nedan och välj sedan det alternativ du anser stämmer bäst med vad du anser.
- Man ska inte ta roten ut både täljaren och nämnaren samtidigt.
- Täljaren blir inte $64$ när man summerar alla termer.
- Man kan inte ha med termen $(3-2)^2$ två gånger i täljaren i samma uträkning.
- Termerna i täljaren under rottecknet står inte i storleksordning, vilket de måste göra.
- Nämnaren är inte korrekt.
- Beräkningen av alla potenser är inte korrekt.
- Man måste kvadrera båda siffrorna i varje parentes var för sig först innan man subtraherar dem.
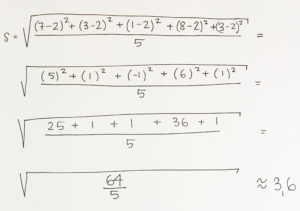Bedömningsanvisningar/Manuell rättning
- +1 e_R Korrekt svar. (Nämnaren är inte korrekt)
- Rättad
Rättar...

c-uppgifter (8)

11. Premium
(0/1/0)
E C A

B 1

P

PL

M

R

K

Hur stor är sannolikheten att en slumpvis vald person har ett blodvärde under $110$ 110 g/l om medelvärdet är $140$ 140 g/l och standardavvikelsen $15$ 15 g/l?

Ange svaret med en decimals noggrannhet.
Svar:

Ditt svar:
Rätt svar: ca $2,3$ % sannolikhet.
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_B Redovisad lösning med korrekt svar. ( $2,3\%$ )

Rättad
Rättar...
12. Premium
(0/2/0)
E C A

B

P

PL 2

M

R

K

I tidtabellen för bussar så står det att det ska ta $16$ 16 min från din busshållsplats till jobbet. Du märker att du är framme vid ganska så olika tider även fast du går hemifrån samma tid varje morgon. Du bestämmer dig för att under två veckor (mån-fre) mäta hur lång tid bussresan verkligen tar, och får följande resultat;

Mån Tis Ons Tors Fre

Vecka 1 21 15 17 19 16

Vecka 2 20 17 16 18 14

Du antar att restiden är normalfördelad. Hur lång tid ska du räkna med att bussresan tar om du bestämmer dig för att du vill ha ca $98\%$ 98% sannolikhet att vara framme den tid du önskar?

Avrunda till hela minuter.
Svar:

Ditt svar:
Rätt svar: Ca $22$ min
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_PL Godtagbar ansats tex beräknar standardavvikelsen.
+1 c_PL Redovisad lösning med korrekt svar. (ca $22$ min)

Rättad
Rättar...
13. Premium
(0/2/0)
E C A

B

P 1

PL

M 1

R

K

Använd ett digitalt hjälpmedel och anpassa en funktion till värdetabellen. Ange sedan värdet för $f(5)$ ƒ (5).
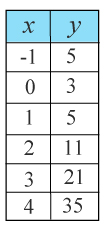Svar:

Ditt svar:
Rätt svar: $f(5)=53$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_M Tar fram korrekt regressionsmodell.
+1 c_P Redovisad lösning med korrekt svar. ( $f\left(5\right)=53$ )

Rättad
Rättar...
14. Premium
(0/2/1)
E C A

B 1

P

PL 1 1

M

R

K
NP

En maskin tillverkar skruvar. Skruvarnas längder är normalfördelade med en standardavvikelse på $0,20$ 0,20 mm. Ungefär $82\text{ }\%$ 82 % av skruvarna har en längd mellan $54,0$ 54,0 mm och $54,6$ 54,6 mm.

Bestäm skruvarnas medellängd.
Svar:

Ditt svar:
Rätt svar: $54,2$ mm eller $54,4$ mm
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_B a) Godtagbar ansats, t.ex. beräknar att det givna intervallet motsvarar tre standardavvikelser
+1 c_PL a) ...med godtagbar fortsättning där en korrekt medellängd anges
+1 a_PL b) ...med i övrigt godtagbar lösning med korrekt svar. ( $54,2$ mm eller $54,4$ mm)

Rättad
Se mer: Normalfördelning
Rättar...
15. Premium
(0/2/1)
E C A

B

P 1

PL 1

M

R 1

K

John beställer diskmedel till sin restaurang på internet hos ett företag som garanterar leverans inom $7\pm2$ 7±2 dagar.

John har ett mycket begränsat lagerutrymme i restaurangen och vill därför minimera antalet dagar med dubbla diskmedelspaket. Vikten på diskmedelspaketen har ett medelvärde på $20$ 20 kg. Skillnaden på paketens vikt är normalfördelade med en standardavvikelse på $1$ 1 kg. Åtgången på diskmedlet i restaurangen är $360$ 360 gram per dag.

Från det att ett nytt paket öppnas, efter hur många dagar måste John beställa ett nytt om han med $97,71$ 97,71% säkerhet inte vill stå utan diskmedel någon gång?
Svar:

Ditt svar:
Rätt svar: Efter $41$ dagar.
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_P
+1 a_PL Korrekt svar. ( $41$ dagar)
+1 c_R

Rättad
Rättar...
16. Premium
(0/2/1)
E C A

B

P

PL

M

R 2 1

K
NP

Demy och Oskar diskuterar hur mycket pengar i kontanter ungdomar i deras egen ålder har med sig till skolan. De bestämmer sig för att göra en undersökning i en klass. Demy och Oskar lämnar ut en lapp med frågan ”Hur mycket pengar har du med dig idag?” och får svar från alla 19 eleverna i klassen. Resultatet redovisar de i lådagrammet nedan.

Undersök i vilket/vilka intervall A-D medelvärdet $M$ M kan ligga. Motivera.

A. $0\le M<6$ 0≤M<6

B. $6\le M<20$ 6≤M<20

C. $20\le M<31$ 20≤M<31

D. $31\le M<112$ 31≤M<112
Svar:

Ditt svar:
Rätt svar: B, C och D
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_R Godtagbart välgrundat resonemang t.ex. visar insikt om hur pengasummorna fördelas i lådagrammets olika kvartiler och att $0,\ 6,\ 20,\ 31$ och $112$ förekommer minst en gång.
+1 c_R Godtagbart välgrundat resonemang t.ex. visar med två korrekta exempel att medelvärdet kan ligga i två av intervallen B, C eller D eller visar att intervall A utesluts och att medelvärdet kan ligga i ett av intervallen B, C eller D.
+1 a_R Godtagbart välgrundat och nyanserat resonemang som leder till slutsatsen att medelvärdet kan ligga i alla tre intervallen B, C och D och att medelvärdet inte kan ligga i intervall A.

Rättad
Se mer: Nationellt prov Matematik 2b vt 2014 DEL D
Rättar...
17. Premium
(0/1/0)
E C A

B 1

P

PL

M

R

K

Ingår bara i c-spår

Hur många observationer ingår i datamängden vars medelvärde motsvara likheten $\overline{x}=$ x= $\frac{\sum_{_{_{k=1}}}^{^{^4}}3k}{4}$ ∑_{_{_k=1}}^{^⁴}3k4
Svar:

Ditt svar:
Rätt svar: $4$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_B Korrekt svar. ( $4$ )

Rättad
Rättar...
18. Premium
(0/1/0)
E C A

B

P 1

PL

M

R

K

Ingår bara i c-spår

Beräkna medelvärdet för $\overline{x}=$ x= $\frac{\sum_{_{_{k=1}}}^{^{^4}}3k}{4}$ ∑_{_{_k=1}}^{^⁴}3k4
Svar:

Ditt svar:
Rätt svar: $7,5$
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_P Redovisad lösning med korrekt svar. ( $7,5$ )

Rättad
Rättar...

a-uppgifter (2)

19. Premium
(0/0/3)
E C A

B 1

P

PL

M

R 1

K 1

Man har gjort lådagram över några statistiska undersökningar. Vilket lådagram motsvarar den datamängd som är mest lik ett normalfördelat material?
Svar:

Ditt svar:
Rätt svar: Lådagram D.
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 a_B Visar förståelse för begreppen.
+1 a_R Godtagbart resonemang med korrekt svar. (Lådagram D)
+1 a_K Lösningen redovisas på ett korrekt matematiksk språk.

Rättad
Rättar...
20. Premium
(0/1/1)
E C A

B

P

PL

M

R 1 1

K
M NP

Emelie gör en statistisk undersökning om sina 18 klasskamraters längd. Hon beräknar sedan medelvärdet av längderna och får det till $175,5$ 175,5 cm.
Emelie presenterar sina resultat i ett histogram. Se nedan.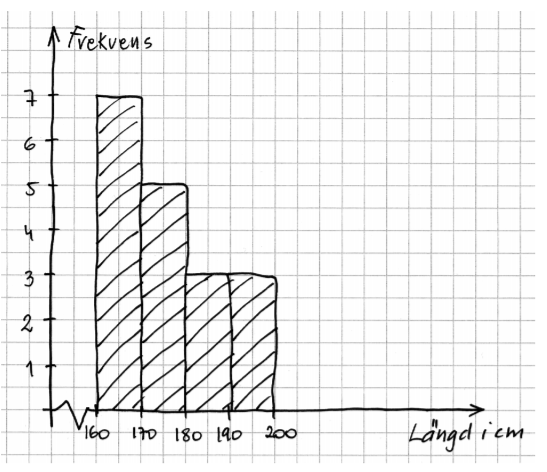

Emelie visar histogrammet för Anton. Han beräknar medelvärdet med hjälp av histogrammet och får då medelvärdet till $176,1$ 176,1 cm. Både Emelie och Anton räknar rätt men får olika medelvärden.

Förklara varför medelvärdet blir olika med de olika metoderna.
Svar:

Ditt svar:
Rätt svar: Se förklaring.
(Korrekta varianter)
Bedömningsanvisningar/Manuell rättning
+1 c_R Godtagbart välgrundat resonemang som innehåller en förklaring av Antons metod som visar insikt om att han använder klassmitten i sina beräkningar
+1 a_R Godtagbart välgrundat och nyanserat resonemang som innehåller en förklaring till varför deras värden blir olika, d.v.s. innehåller ett resonemang om att Emelie använder exakta värden i sin beräkning vilket ger det korrekta medelvärdet och att Anton beräknar medelvärdet från varje stapels klassmitt vilket inte nödvändigtvis motsvarar hela stapelns medelvärde.

Rättad
Se mer: Histogram Repetition Statistik
Rättar...

Nästa lektion: Kapiteltest – Statistik Ma2a

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

PROVA GRATIS

Så hjälper Eddler dig:

Videor som är lätta att förstå Övningar & prov med förklaringar

Allt du behöver för att klara av nationella provet

Eddler

VÅR TJÄNST

POPULÄRA KURSER

FÖRETAGSINFO

Eddler AB
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg
info@eddler.se

Säker SSL-server

Vad är detta?

Här hittar du matematiska symboler som kan användas när du ställer frågor på forumet eller kommenterar. När du klickar på symbolen markeras denna, kopiera genom klicka med höger musknapp eller använda kortkommandot Ctrl-C (PC) / cmd-C (Mac)

Förhandsvisning Latex:

Latexkod:

	Mån	Tis	Ons	Tors	Fre
Vecka 1	21	15	17	19	16
Vecka 2	20	17	16	18	14

Matematik 2

Välj kurs

KURSER /

Matematik 2

/ Statistik

Blandade övningar - Statistik

Författare:Simon Rybrand

Allt du behöver för att klara av nationella provet

Allt du behöver för att klara av nationella provet

Innehåll

Fördjupning Ma2c Summatecknet som skrivsätt vid beräkning av medelvärde

Medelvärde

Lösning

Exempel 2

Lösning

Kommentarer

Lisa Rahmani

Simon Rybrand (Moderator)

Lisa Rahmani

Janne

Pedro Veenekamp

GenIT

Simon Rybrand (Moderator)

Endast Premium-användare kan kommentera.

1.

2.

3.

Allt du behöver för att klara av nationella provet

Allt du behöver för att klara av nationella provet

4. Premium

5. Premium

6. Premium

7. Premium

8. Premium

9. Premium

10. Premium

11. Premium

12. Premium

13. Premium

14. Premium

15. Premium

16. Premium

17. Premium

18. Premium

19. Premium

20. Premium

Eddler

VÅR TJÄNST

POPULÄRA KURSER

FÖRETAGSINFO

LADDAR DOKUMENT...

LADDAR GEOGEBRA...

Fördjupning Ma2c
Summatecknet som skrivsätt vid beräkning av medelvärde