Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 2b
/ Algebra – Matematik 2
Konjugatregeln och kvadreringsreglerna
Innehåll
Förenkla uttryck
När man arbetar med att förenkla uttryck händer det att man stöter på uttryck där en parentes som innehåller två termer är kvadrerad. För att underlätta arbetet med sådana uttryck kan kvadreringsreglerna vara till hjälp.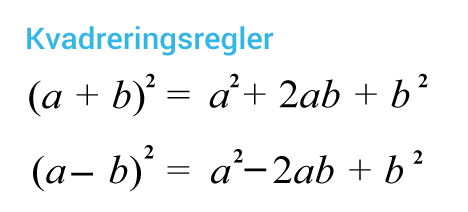
Om du istället har två konjugat som multipliceras använder du konjugatregeln.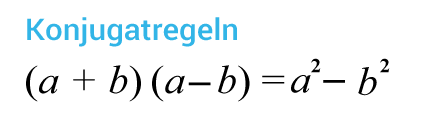 
Dessa regler finns framförallt för att effektivisera och snabba upp hanteringen av algebraiska uttryck. Det är därför bra att träna så att du känner dig säker på hur dessa regler fungerar.
Reglerna är framtagna utifrån den utvidgade distributiva lagen och vi kommer att presentera dem närmre här.
Kvadreringsreglerna
Det finns två stycken kvadreringsregler. Dessa är följande.
Kvadreringsreglerna
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
Skillnaden mellan dessa bägge regler är alltså att den andra regeln hanterar då vi har ett minustecken istället för ett plustecken i parentesen. Dessa bägge regler kan även användas för att faktorisera, d.v.s. att man bryter ut en term ur ett uttryck för att förenkla det. Vi kan visa att den första regeln stämmer genom att använda den utvidgade distributiva lagen.
Den utvidgade distributiva lagen
Arean av en kvadrat med sidan $\left(a+b\right)$(a+b) kan visa att lagen stämmer genom att beskriva kvadratens area som en helhet och som summan av fyra delar.
$ (a+b)^2= (a+b)(a+b)=$
$ a^2+ab+ba+b^2=$ $a^2+2ab+b^2 $
Kvadrering av ett binom kommer alltså alltid ge första termen i kvadrat, dubbla produkten av de två termerna och andra termen i kvadrat.
Enda skillnaden mellan kvadreringsreglerna är att addition mellan termerna ger att alla termerna efter utvecklingen är positiva, medan subtraktion mellan termerna ger att dubbla produkten av de två termerna istället ska subtraheras från kvadraterna.
Nu följer några exempel där vi använder reglerna för att utveckla uttryck.
Exempel 1
Utveckla uttrycket $(x+9)^2$ med hjälp av kvadreringsreglerna.
Lösning
$(x+9)^2=x^2+2\cdot x\cdot9+9^2=x^2+18x+81$(x+9)2=x2+2·x·9+92=x2+18x+81
Ett vanligt fel många gör när de börjar utveckla uttryck med kvadreringsreglerna är att glömma bort att hela termerna ska kvadreras. Om en term består av flera faktorer gäller potensregeln $\left(a\cdot b\right)^2=a^2b^2$(a·b)2=a2b2 .
Exempel 2
Utveckla uttrycket $(6x-4)^2$ med hjälp av kvadreringsreglerna.
Lösning
$(6x-4)^2=(6x)^2-2\cdot 6x\cdot 4+4^2=36x^2-48x+16$
Vi observerar att hela termen $6x$6x, alltså både sexan och $x$x:et, ska kvadreras vid utvecklingen av uttrycket. Det ger att första termen i utvecklingen blir $\left(6x\right)^2=6^2\cdot x^2=36x^2$(6x)2=62·x2=36x2 .
Konjugatregeln
Inom matematiken är ett binom ett uttryck med två termer. När man jobbar med algebra är konjugatet till ett binom, det binom som är exakt likadant, med undantaget att tecknet mellan de två termerna är motsatt.
Tillexempel är konjugatet till $x+4$x+4 binomet $x-4$x−4 och konjugatet till $7-3a$7−3a lika med binomet $7+3a$7+3a.
Om ett uttryck på formen $(a+b)$ multipliceras med dess konjugat $(a-b)$ ges resultatet $ a^2-b^2 $. Detta sammanfattas i konjugatregeln.
Konjugatregeln
$(a+b)(a-b)=a^2-b^2$
Även denna regel kan visas att den stämmer genom att utveckla följande med hjälp av den utvidgade distributiva lagen.
Den utvidgade distributiva lagen
$ (a+b)(a-b) $ $= a^2 -ab + ab – b^2 $ $= a^2-b^2 $
Nu följer några exempel där vi använder reglerna för att utveckla uttryck.
Exempel 3
Utveckla uttrycket$(x+8)(x-8) $ med hjälp av konjugatregeln.
Lösning
Parenteserna är varandras konjugat och vi kan använda konjugatregeln.
$(x+8)(x-8) =x^2-8^2=x^2-64$
Förenkla uttryck med hjälp av konjugat och kvadreringsregeln
Tänk på att alltid svarar med ett förenklat uttryck. Detta görs genom att termer som är av samma sort läggs samman efter att man utvecklat uttrycket.
Exempel 4
Förenkla $2\left(x-2\right)^2-2x\left(x-3\right)$2(x−2)2−2x(x−3)
Lösning
Vi utveckla först kvadraten, ”upphöjt till två” med kvadreringsregeln innan vi multiplicerar inte tvåan och får
$2\left(x-2\right)^2-2x\left(x-3\right)=2\left(x^2-4x+4\right)-2x\left(x-3\right)$2(x−2)2−2x(x−3)=2(x2−4x+4)−2x(x−3)
Nu multiplicerar vi in i parenteserna
$2\left(x^2-4x+4\right)-2x\left(x-3\right)=2x^2-8x+8-2x^2+6x$2(x2−4x+4)−2x(x−3)=2x2−8x+8−2x2+6x
Slutligen förenklar vi uttrycket genom att addera och subtrahera termer av samma sort.
$2x^2-8x+8-2x^2+6x=8-2x$2x2−8x+8−2x2+6x=8−2x
I kommande lektioner kommer vi träna på att använda konjugat och kvadreringsreglerna ”baklänges” för att göra det vi kallar för att faktorisera.
Exempel i videon
- Utveckla $(x+6)^2$(x+6)2
- Utveckla $(x-3)^2$(x−3)2
- Utveckla $(3x-x^2)^2$(3x−x2)2
- Utveckla $(x+3)\cdot(x-3)$(x+3)·(x−3)
- Utveckla $(x^2+x)\cdot(x^2-x)$(x2+x)·(x2−x)
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (23)
-
1. Premium
Vilken regel ska du använda för att snabbt och smidigt utveckla uttrycket nedan?
$(x+3)^2$(x+3)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Första kvadreringsreglen kvadreringsreglerna utveckla uttryckRättar...2. Premium
Utveckla uttrycket $(x+3)^2$(x+3)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra förenkla uttryck kvadreringsreglerna utveckla uttryckRättar...3. Premium
Utveckla uttrycket $(x+8)^2$(x+8)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra förenkla uttryck kvadreringsreglerna utveckla uttryckRättar...Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut!4. Premium
Utveckla uttrycket $(x+2)^2$(x+2)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...5. Premium
Mimmi har utvecklat uttrycket $\left(a+4\right)\left(a-4\right)$(a+4)(a−4) och fått svaret $a^2-16$a2−16.
Har hon gjort rätt?Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra konjugatregelnRättar...6. Premium
Vilken regel ska du använda för att snabbt och smidigt utveckla uttrycket nedan?
$(x+3)(x-3)$(x+3)(x−3)
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra konjugat konjugatregeln utveckla uttryckRättar...7. Premium
Utveckla uttrycket $(x+3)(x-3)$(x+3)(x−3)
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra konjugat konjugatregeln utveckla uttryckRättar...8. Premium
Utveckla uttrycket
$(x-8)^2$(x−8)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra Kvadreringsreglen kvadreringsreglerna utveckla uttryckRättar...9. Premium
Vilken regel ska du använda för att snabbt och smidigt utveckla uttrycket nedan?
$(7-y)^2$(7−y)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...10. Premium
Utveckla uttrycket $(7-y)^2$(7−y)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra andra kvadreringsregeln kvadreringsregeln utveckla uttryckRättar...11. Premium
Utveckla uttrycket $(z+5)(z-5)$(z+5)(z−5)
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra konjugatregeln Konjugatregeln och kvadreringsreglerna – utveckla uttryck Matematik 2Rättar...12. Premium
Utveckla uttrycket
$(a+1)^2$(a+1)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra kvadreringsregler kvadreringsreglerna utveckla uttryckRättar...13. Premium
I vilket eller vilka av uttrycken är faktorerna varandras konjugat?
A. $(x+2)(x-5)$(x+2)(x−5)
B. $(x+4)^2$(x+4)2
C. $(x+3)(x-3)$(x+3)(x−3)
D. $\left(x+2\right)\left(x+2\right)$(x+2)(x+2)
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Matematik 2 nationellt prov Nationellt prov Ma2b vt15 ProvRättar...14. Premium
Förenkla följande uttryck med hjälp av kvadreringsreglerna
$\left(x+3\right)^2+\left(5-x\right)^2$(x+3)2+(5−x)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra förändra uttryck konjugatregeln konjugatreglernaRättar...15. Premium
Jens har utvecklat uttrycket $\left(2x-3\right)^2$(2x−3)2 och har fått det till $4x^2-12x-9$4x2−12x−9.
Har han gjort rätt?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra kvadreringsregelnRättar...16. Premium
Utveckla uttrycket
$(2x+4)^2$(2x+4)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...17. Premium
Utveckla $\left(5x-5\right)^2$(5x−5)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra kvadreringsregeln utveckla uttryckRättar...18. Premium
Vad ska stå i stället för @ för att likheten ska stämma?
$\left(@+2\right)\left(@-2\right)=9x^2-4$(@+2)(@−2)=9x2−4
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra algebraiska uttryck förenkla konjugatregeln utveckla uttryckRättar...19. Premium
Lös följande ekvation
$\left(x-4\right)^2-\left(x+2\right)\left(x-2\right)=0$(x−4)2−(x+2)(x−2)=0
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra förenkla uttryck förenkling konjugatregeln kvadreringsregelnRättar...20. Premium
Utveckla och förenkla
$\left(x+3\right)^2+\left(x-3\right)^2-2x^2$(x+3)2+(x−3)2−2x2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra algebraiska uttryck förenkla konjugatregeln kvadreringsregeln utveckla uttryckRättar...21. Premium
Förenkla följande uttryck så långt som möjligt.
$8y+\left(4-y\right)^2$8y+(4−y)2
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra algebraiska uttryck förenkla förkortaRättar...22. Premium
Utveckla uttrycket $\left(3x+4y\right)^2$(3x+4y)2 med första kvadreringsregeln.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra kvadreringsregeln utveckla uttryck utvecklingRättar...23. Premium
Vilket av följande uttryck beskriver arean för en rektangel där långsidans och kortsidans längder skiljer sig med $10$10 cm?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra konjugatregeln ma2 Matematik 2 modellering Problemlösning AlgebraRättar...c-uppgifter (14)
-
24. Premium
Förenkla uttrycket så långt som möjligt
$\left(x-6\right)^2-2\left(x+6\right)\left(x-6\right)-100$(x−6)2−2(x+6)(x−6)−100
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Algebra förenkla uttryck förenkling konjugatregeln kvadreringsregelnRättar...25. Premium
Utveckla uttrycket $(x+2)^2(x-2)$(x+2)2(x−2)
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...26. Premium
Förenkla följande uttryck så långt som möjligt
$\left(x+5\right)^2-\left(5+x\right)\left(5-x\right)$(x+5)2−(5+x)(5−x)
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Konjugatregeln och kvadreringsreglerna Förenkla algebraiska uttryck -
-
anders persson
Gällande fråga 35 så skriver ni ”Vi kan skriva om (x−a) till (−a+x), vilket man kan göra enligt kommutativa lagen, och kan då få fram a på följande vis”
Men jag har svårt att förstå kommutativa lagen här. Jag vet att -4*4=4*-4 är detsamma. Men kommutativa lagen säger också att man inte kan ändra tecken när det är en operatör framför ”-” dvs 7-3 ≠ 3-7. Men jag kommer inte ihåg att kommutativa lagen någonsin har nämnt detta. För som jag förstår det så blir det ungefär
a-b=a+(-b)=(-b)+a
Michael Englund
Tar inte emot a=±2 som svar.
Anna Eddler Redaktör (Moderator)
Fixat!
Beatrice Nielsen
Fråga 18 ger fel svar om man skriver ”@=3x”.
I övriga frågor där de efterfrågar vad tex ”n” är har man fått fel om man INTE har skrivit n=3x.
Fick rätt när jag bara skrev ”3x”
Anna Eddler Redaktör (Moderator)
Hej Beatrice,
bra notering. Sant att du behöver ha med variabeln nära du löser en ekvation för att få rätt. I denna uppgift var frågan ”Vad ska stå i stället för …?” vilket leder till att du inte nödvändigtvis behöver ha med tecknet och likheten. Men jag la till det som ett korrekt alternativ för det bör ju inte ge fel även om det in är nödvändigt.
Emily Wickenberg
Hej! Uppgift 8 tror jag kan vara fel här.
-8^2 är väl ändå -64 och inte ett positivt tal?
Anna Eddler Redaktör (Moderator)
Hej Emily,
enligt konjugatregeln så motsvarar sista termen endast $8^2$. Det beror på att du egentligen kvadrerar $(-8)$.
Regeln kommer från följande utveckling.
$(x-8)^2=(x-8)(x-8)=$$x\cdot x + x\cdot (-8) + (-8)\cdot x + (-8) \cdot (-8)=$$x^2-8x-8x+64=$$x^2-16x+64=$
Den sista termen motsvarar alltså produkten $(-8)(-8)=64$
Hoppas det gick att hänga med på.
Anna Eddler Redaktör (Moderator)
Hej Ronja,
du behöver även ange rätt enhet för att få korrekt svar!
HPvinst yes
Uppgift 26:
Hur kan man plocka bort trean med minus framför sig i steg 1 genom att sätta parentes runt dom mindre parenteserna.
Anna Eddler Redaktör (Moderator)
Trean har inte plockats bort, utan brutits ut;)
Vi börjar nämligen förenklingen med att bryta ut en trea i båda termerna i täljaren för att sedan förkorta bort den mot nämnaren.
Jonas Hultberg
Det står att 41209 är fel.
Anna Eddler Redaktör (Moderator)
Hej Jonas,
kan det vara så att du missat skriva med enheten? Utan den ger inte systemet rätt…
TE20a Habiallah Naseri
Hej!
Jag undrar bara allmänt, på vilken nivå kan man ligga i matte kurser om man enbart pluggar i eddler?
Jag tycker inte om att plugga så mycket i böcker som man gör i skolan och tycker att eddler är mycket bättre.
Så på vilken nivå kan jag tänka mig ligga på om jag enbart pluggar i eddler och lärarens genomgångar?
Anna Eddler Redaktör (Moderator)
Hej,
det beror lite på hur du jobbar:)
Om du förstår alla genomgångar på Eddler och förstår och löser alla uppgifter på Eddler med fullständiga förklaringar och tydlig skriftliga resonemang har du alla förutsättningar att nå ett A i kurserna Ma1abc-3bc. I Ma4 och Ma5 bör du komplettera något med ytterligare A-uppgifter.
Men då gäller det verkligen att du förstår på djupet och har omvandlat kunskapen till din egen! Det gör du bäst genom att skriva ner dina lösningar på papper och jämför med förklaringarna och bedömningsanvisningarna på uppgifterna. Tydliga redovisningar är en viktig del av de högre betygens kriterier.
Kul att du gillar Eddler! Lycka till.
Alexandra Pope
Hej!
Står i förklaringen till fråga 5 att det är ett minustecken i parentesen,
men det finns ju inte?
Talet är ju (a+1)^2?
Mvh
Alexandra
Joacim Jocke Dahl
Hej!
Mitt svar a^2+2a+2 blir fel på uppgift 5. När jag kollar på förklaringen så verkar det som att den förklarar en helt annan uppgift?
David Admin (Moderator)
Hej Joacim,
konstanten ska varar $1$ och inte $2$. Det är ju värdet av $1^2$ som ger rätt konstantterm.
Erik Cairns
$10x+2+x^2$ räknas inte trots att det är rätt svar
Anna Admin (Moderator)
Hej Erik,
vi lägger till ditt svar som ett korrekt svar.
Men jag vill ändå passa på att kommentera att man vanligtvis anger ett svar med fallande ordningen på graden på termerna. Alltså att den termen med störst exponent står först och sedan följer termerna i ordning med mindre och mindre exponenter.
I fallet du beskriver skulle det vara $x^2+10x+2$.
Att man inom matematiken föredrar detta sätt att skriva, beror på att det skapar en tydlighet. Det är då lättare att se vad för slags polynom uttrycket beskriver, vilket kommer underlätta i arbetet med funktionsanalys framöver.
Men du har rätt. Ditt svar är också korrekt.
Saeed Khadora
fråga 11
15^2=15^2-5^2+5^5 måste vara 15^2=15^2-5^2+5^2
Anna Admin (Moderator)
Japp. Tack för ditt påpekande. Uppgiften är korrigerad.
Christian Vittaniemi
Fråga 13 har ett fel i din förklaring.
15^2=15^2-5^2+5^5. Det ska nog stå 5^2=15^2-5^2+5^2.
Alltså inte fem upphöjt till 5, utan 5 upphöjt till två i sista termen.
Med vänlig hälsning Christian
Christian Vittaniemi
Fråga 11 menar jag, sista frågan.
Krister Ristvedt
Kvadreringsreglerna, exempel 1. Tror det saknas ett = tecken mellan 4^2 och x^2. Tror även att 4^2 kommer ifrån nästa exempel, och att ni menar 9^2 egentligen. Var lite förvirrad där en stund då jag undrade var 4^2 hade smugit in någonstans!
Simon Rybrand (Moderator)
Japp, det saknades där, det är fixat!
Krisztina Tofalvi
Jag förstår inte förklaringen till övn. upg 7.
Simon Rybrand (Moderator)
Hej, var är det som du fastnar?
Hanna Josefsson
Jag skulle hemskt gärna också ha en närmre förklaring på uträkningen i upg. 7. Kan du förtydliga själva uträkningen det det endast står ”nu multiplicerar vi ihop parenteserna som vanligt”. Där låser det sig i mitt huvud, tack på förhand 🙂
Simon Rybrand (Moderator)
Hej Hanna
Jag har lagt till 2 steg på förklaringen, hoppas att det hjälper dig vidare!
Jon Abrahamsson
Hur vet jag vad jag skall använd? När jag började med etta kapitel så påminde detta mig om distribution lagen och utvidgade distribution lagen. Jag hade antagligen suttit och försökt med det…. jag ser inte på ett utryck vad jag skall göra/använda
Simon Rybrand (Moderator)
Hej
Det kan krävas lite träning och att man ofta går tillbaka till formlerna för att kolla hur de ser ut innan man känner sig trygg med dem.
Tänk särskilt på att undersöka hur de olika formlerna är konstruerade.
Jon Abrahamsson
I uppgift 3 & 6 blir det en parantes, varför? Jag missar då att räkna ut den, får då ut just 2xikvadrat och 3xikvadrat. Vad missar jag? Och även vad är skillnaden mellan utveckla och förenkla? Har svårt att veta var jag skall stanna
Simon Rybrand (Moderator)
Det är för att en term är ”hela” 3x och för att visa att vi skall upphöja hela 3x med två. Dvs (3x)^2=(3x)·(3x)=3^2x^2=9x^2
Utveckla – Multiplicera ihop parenteser och beräkna kvadrater
Förenkla – Lägga samman / summera termer av samma sort.
carlsson_elias@hotmail.com
Hej! Jag har fått för mig att:
(a+b)^2 förenklas a^2+b^2
Men detta är bara något jag fått för mig eller stämmer detta i något sammanhang? Jag förstår inte riktigt skillnaden på förenkla, utveckla och faktorisera..
Jesper Westin
(a+b)^2=a^2+2ab+b^2
Om det är ett ”-” i parantesen så blir det a^2-2ab+b^2.
Noor Noor
Gör han inte fel i exempel 3 i videon ? hur får han 3X^2 till 9x^2 ??
Simon Rybrand (Moderator)
Hej, tänk på att det står $(3x)^2$ dvs med en parentes runt 3x. Det här är samma sak som
$ (3x)⋅(3x) = 3⋅3⋅x⋅x=9x^2 $
Philosofen
Sitter och klurar på det här exemplet just nu. Borde inte 3x^2 = 9x? (Varför 9x^2)?
Simon Rybrand (Moderator)
Hej, det är viktigt att förstå att $ 3x^2 $ inte är lika med $ (3x)^2 $ där både 3 och x skall upphöjas med 2 och inte bara x.
Så om du har $ (3x)^2 = 3^2x^2 = 9x^2 $.
Hoppas att detta hjälper dig vidare!
Jpersson
Hej, jag tampas med en uppgift som vill att jag genom att använda konjugatregeln skall hitta ett bra sätt att beräkna värdet av:
41 x 39
Hur gör man detta?
Jag skall använda (80+3)(80-3) för att hitta en bra lösning men finner inga sätt.
Simon Rybrand (Moderator)
Hej
Kan du tänka att du skriver det som
$ 41⋅39 = (40+1)(40-1) $
Nu använder vi konjugatregeln och skriver det som
$ 40^2-1^2 = 1600-1 = 1599 $
Ditte Jardmark
I sista frågan (fråga 8) varför är svar 3 felaktigt?
Simon Rybrand (Moderator)
Där har du $(x-2)^2$ vilket kan utvecklas till
$(x-2)^2 = x^2-4x+4 $
Detta går inte att förenkla till $x^2-4$ då vi har $-4x$ i detta.
Mikael144600
Hej!
Angående fråga 6, varför blir -1^2=-1. Borde inte svaret bli +1 (dvs 9x^2+1)?
Simon Rybrand (Moderator)
Hej
Nej det blir det inte, det bästa sättet att se detta är nog att inte använda konjugatregeln utan att multiplicera ihop parenteserna (utvidgade distributiva lagen). Då blir det tydligt:
$(3x+1)(3x-1) = 9x^2 -3x + 3x – (1^2) $
$ = 9x^2-1 $
Tänk också på att det blir $-(1^2) = -1 $.
Caroline
Angående konjugatregeln i början på videon; ni säger att det ska (a+b)(a-b) = a^2 + 2ab – 2ab – b^2. Jag förstår inte var just 2ab kommer in? Ska det inte se ut såhär a^2 + ab – ab – b^2? Var kommer 2:orna till ab ifrån?
(a+b)(a-b) = a * a, a * -b, b * a, b * -b = a^2 – ab + ab – b^2 tänker jag? Även kring att minus ab ska komma före plus ab om ni kollar min sista uträkning här.
Tack!!! 🙂
Simon Rybrand (Moderator)
Hej, tack för att du kommenterade detta. Det är självklart ett skrivfel där i videon som vi skall åtgärda under dagen.
(uppdatering: det är korrigerat)
Caroline
Toppen!
Undrar också på samma ställe, det står ju att svaret blir a^2 + ab – ab – b^2 men ska inte det första plus-tecknet byta plats med minus-tecknet i mitten? Eftersom att det är a*-b = -ab??
Eller radar man upp alla positiva och sedan negativa? Det spelar kanske ingen roll i vilken ordning de ligger?
/Carro
Simon Rybrand (Moderator)
Hej
Jo det skall vara i den ordningen du nämner, felrättningen gick för snabbt där.. 😉 Vi ser till att ordna detta.
BotenAnnie
hej ! X^4 – X^2 (sista ex i videon) kan man inte utv det mer ? blir det inte X^4 – X^2 = X^2?
Robin Saetre
När det fryser kan man trycka på hd knappen så laddar den om utan att man behöver ladda om hela sidan 🙂
Petter Östergren
Funkade efter jag rensade catchen på datorn… Skumt,
Men men
Ska man använda den reglen på en sån här ?
(1+x-x^2)xy
Simon Rybrand (Moderator)
Hej,
Det beror lite på vad du skall göra med uttrycket. Skall du utveckla det (multiplicera in i parentesen) eller faktorisera det?
Om du utvecklar det så får du
$(1+x-x^2)xy=xy+x^2y-x^3y$
maggie liew
Hej kan ni visar mig hur man lösa denna frågan?
6+y/y – Y/2 = 3
Simon Rybrand (Moderator)
Hej
Om det inte skall vara en parentes någonstans i vänsterledet så löser du ekvationen enligt följande:
$6+y/y –y/2 = 3 ⇔ $
$6+1–\frac{y}{2} = 3 ⇔ $
$\frac{y}{2}=4 ⇔$
$y=8$
Petter Östergren
Krånglar tyvärr ännu.
Nathalie Larsson
Märker att det fryser och stannar till mitt under videogenomgångarna för mig med, men ja försöker återkolla klippen så jag dör ju ej:P men skjulel vara bra om det åtgärdades^^
Simon Rybrand (Moderator)
Hej,
Vi håller på och jobbar med att en del upplever problem med detta. Förhoppningsvis kommer det att blir bättre redan under dagen.
Om du fortfarande har problem sedan så hör av dig till support@matematikvideo.se.
dinmamma777
Hej
Videoklippen fryser lite då och då efter uppdateringen.
Simon Rybrand (Moderator)
Hej, kontakta oss gärna om du har problem så kan vi hjälpa dig vidare!
Endast Premium-användare kan kommentera.