Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik Högstadiet
/ Volym
Volym
Innehåll
Volym är ett mått på hur mycket en tredimensionell geometrisk figur rymmer. Volym mäts i enheten volymenheter.
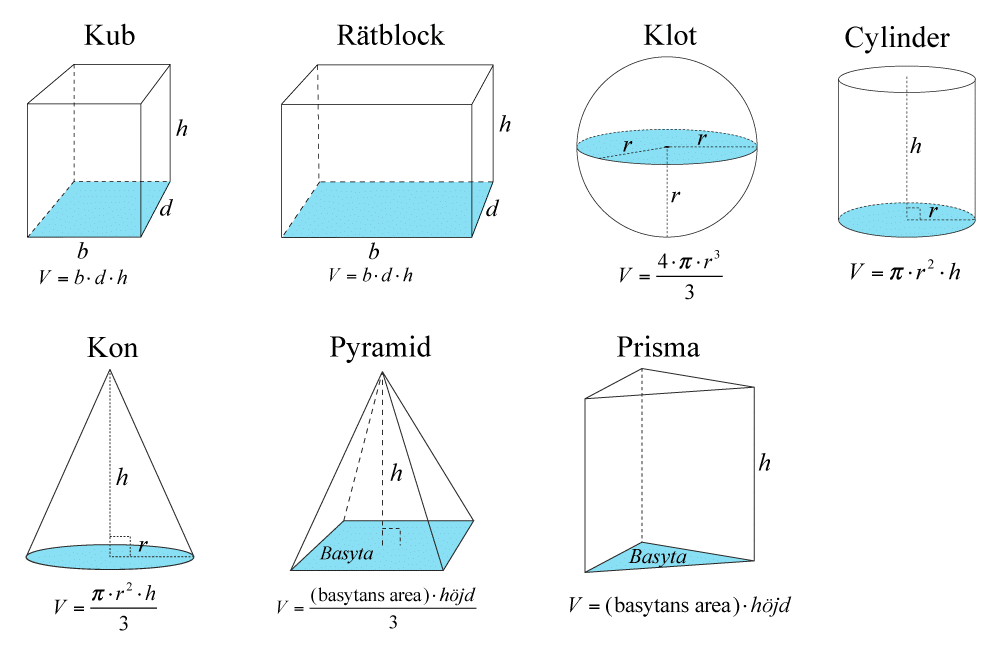
Tidigare har vi lärt oss om geometriska figurer i två dimensioner. Det kan exempelvis vara kvadrater, rektanglar eller cirklar. Dessa har oftast en bredd och en höjd men inget djup. Om vi lägger till en tredje dimension, ett djup, får vi en geometrisk figur som har en volym. Det kan exempelvis vara en kub, ett rätblock eller en cylinder.
Volym beskriver alltså hur mycket som ryms i ett föremål. Vanliga sådana föremål i vardagen är exempelvis ett mjölkpaket som rymmer $1\text{ }liter=1\text{ }dm^3$1 liter=1 dm3 eller en colaburk som rymmer $33\text{ }cl=330\text{ }cm^3$33 cl=330 cm3.
Enhet för volym
Den enhet som används för att mäta storleken på en volym kallas för volymenheter (förkortas v.e).
Exempel på volymenheter:
$cm^3,\text{ }m^3,\text{ }dm^3,\text{ }liter\text{ }(l),\text{ }deciliter\text{ }(dl),\text{ }och\text{ }milliliter\text{ }(ml)$cm3, m3, dm3, liter (l), deciliter (dl), och milliliter (ml)
Vi uttalar exempelvis $cm^3$cm3 som kubikcentimeter och skriver trean upphöjd för att visa att detta är en volym i tre dimensioner.
Standardenheten (SI-enhet) för volym är kubikmeter $m^3$m3.
I andra länder används andra volymenheter än de vi använder i Sverige. I USA är det exempelvis vanligt att använda gallons (us gallons) där 1 us gallon = 3,7854 liter. Vi kan fördjupa oss om volymenheter här.
Exempel på geometriska figurer med volym
Nedan samlar vi ett antal geometriska figurer och hur deras volym beräknas.
Kub
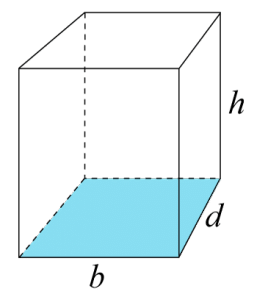
En kubs sidor är alla lika långa. Kuben består av 6 stycken lika stora kvadrater enligt bilden ovan. För att beräkna dess volym används följande formel:
$\text{Volym}=\text{bas}\cdot\text{djup}\cdot\text{höjd}$Volym=bas·djup·höjd
Då alla sidor $s$s är lika långa går det även att skriva volymen som $Volym=s\cdot s\cdot s=s^3$Volym=s·s·s=s3.
Rätblock
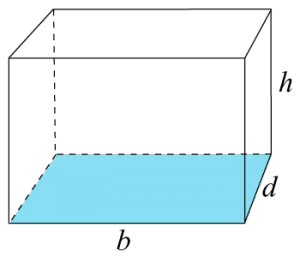
Ett rätblock kan beskrivas som en låda. Till skillnad från kuben så kan den ha sidor som är olika långa.
$\text{Volym}=\text{bas}\cdot\text{djup}\cdot\text{höjd}$Volym=bas·djup·höjd
Cylinder
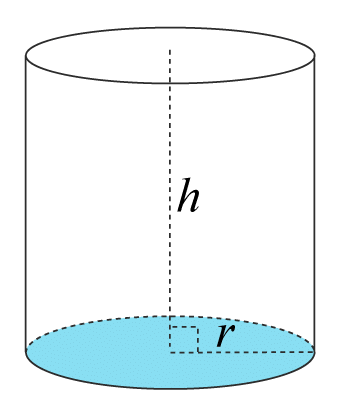
En cylinder kan beskrivas som en tunna eller en läskburk. Cylinderns basytor, både uppe och nere, består av cirklar som binds samman med en höjd. För att beräkna volymen utgår vi från cirkelns area och multiplicerar med höjden.
$\text{Volym}=\pi\cdot r^2\cdot h$Volym=π·r2·h
Klot eller Sfär
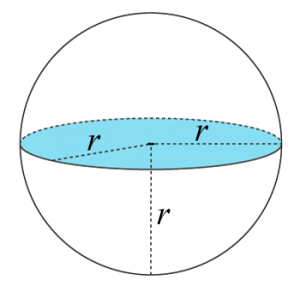
Ett klot är en geometrisk kropp som begränsas av radiens avstånd från klotets centrum. En sfär är den yta som omsluter klotet. Vi kan tänka att klotet består av allt från centrum ut till sfären.
$\text{Volym}=$Volym= $\frac{4\cdot\pi\cdot r^3}{3}$4·π·r33
Kon
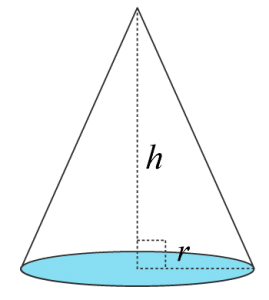
En kon ser ut som en partyhatt eller en glasstrut. Den består av en cirkulär basyta, en spets och en höjd som binder samman dem.
$\text{Volym}=$Volym= $\frac{\pi\cdot r^2\cdot h}{3}$π·r2·h3
Pyramid
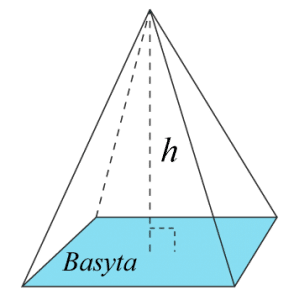
Pyramider har en basyta som är en månghörning. Månghörningen kan ha tre eller flera sidor. Sedan binds månghörningens hörn ihop med en spets till en volymkropp.
$\text{Volym}=$Volym= $\frac{\left(\text{basytans area}\right)\cdot h}{3}$(basytans area)·h3
Prisma
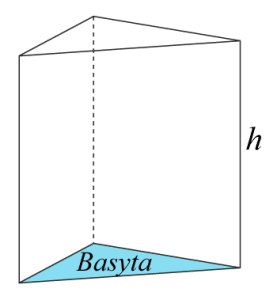
Ett prisma kan sägas ha två basytor bestående av månghörningar som binds samman i dess hörn med en höjd. Månghörningarna kan ha tre eller fler sidor.
$\text{Volym}=\text{basytans area}\cdot\text{höjd}$Volym=basytans area·höjd
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (4)
-
1. Premium
Vad menas med att beräkna volymen för en kub?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: VolymRättar... -
2. Premium
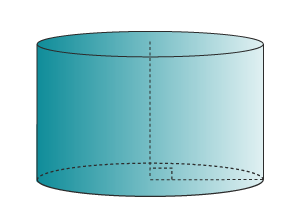
Vad kallas den geometriska kroppen i figuren?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: VolymRättar... -
3. Premium
Vad kallas den geometriska kroppen i figuren?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: VolymRättar... -
4. Premium
Vad kallas den geometriska kroppen i figuren?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: VolymRättar...
Jonas Johansson
Undrar på fråga 7 vad du menar med ” rätblock där sidorna förhåller sig som 1:2:3 mot varandra ” ?
Ane Kongo
Hej! Jag hade rätt svar på fråga 4 som är 1030. Jag skrev 1030 kr och fick svar att svaret är fel? Varför?
Alexandra Trudel
Hej,
Bra sida!
Dock får jag fel på fråga 8 för att jag inte kan skriva ut kubiken med upphöjd trea. Sitter på en mac-dator och det kvittar varifrån jag klistrar in den upphöjda trean, stannar inte kvar i svarsfältet utan får då ist 48dm3 hur jag än gör, kanske ett sådant svar kunde räknas som godkänt ändå?
Arsema Kifle
hej, igen tranar pa gamla prov och denna fraga forstar inte hur m=n
2^n=3^m
jag trodde att m 2
Arsema Kifle
Hej, kan du forklara du man kan losa denna fraga?
Vad är x om √30x = √3 · x och x > 0
tack pa forhand!
Johan
hej
Höjden på cylindern enligt bilden i uppgift 6 måste väl vara 2r (3r-r)
Berkan991
Hej!
På fråga 2 så tog jag 0,3×0,3 och det blir 0,09 sen tog jag gånger 1.2 och det blir 0,108 och ni fick 0,34 hur?
Frisjo
Hej
Det vore bra om du anpassade frågorna i Högskoleprovs-delen till huvudräkningsmöjliga med en svårighetsgrad i paritet m hp. Detta då det är en förutsättning när man gör provet. I övrigt är ju huvudräkning bra träning för alla.
hälsningar Frida
mattias.ram
Hejsan
Superbra sida!
En fråga bara jag förstår uppgifterna men har svårt att räkna ut dem i huvudet, är tanken att man skall klara det utan miniräknare?
Mvh
Simon545
Hej
Det står fel på sista uppgiften. I frågan står det om bollen ”Bollens radie är 10,83cm”. I svaret räknar ni med att bollens radie är 10,38.
Margareta
Tack, tack för himla bra genomgångar!!! Man fattar så bra efter att ha lyssnat på dessa tydliga förklaringar.Toppen!
Endast Premium-användare kan kommentera.