Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
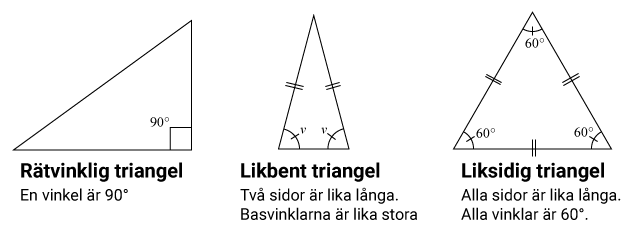
I en rätvinklig triangel är en vinkel 90°. I likbenta trianglar är två sidor lika långa och basvinklarna lika stora. I liksidiga trianglar är alla sidor lika lång och alla vinklar är 60°.
I den här lektionen går vi igenom tre olika typer av trianglar: Rätvinkliga trianglar, likbenta trianglar och liksidiga trianglar. Dessa tre typer av trianglar har några viktiga egenskaper att känna till.
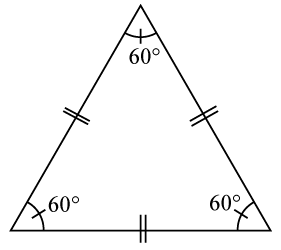
Ett vanligt sätt att markera att två vinklar eller två sidor är lika stora eller långa är att rita små markeringsstreck över dem. Här har vi markerat att de två vinklarna är lika stora genom varsitt sträck genom vinkelbågen. Vi visar även att sidorna är lika långa genom att rita två streck genom dem. Vi ritar två streck för att vi inte skall blanda ihop det med vinkelbågarna.
Rätvinklig triangel
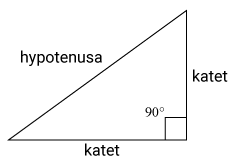
En rätvinklig triangel är en triangel som har en vinkel som är 90∘90∘, dvs den har en rät vinkel. De två räta sidorna kallas i en rätvinklig triangel för kateter och den sneda sidan kallas för hypotenusa.
Exempel 1
Bestäm storleken av vinkeln vv.
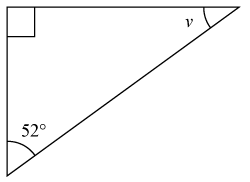
Lösning
Triangeln är rätvinklig så då vet vi vinklarna 90∘90∘ och 52∘52∘.
Vi får att v=180∘−90∘−52∘=38∘v=180∘−90∘−52∘=38∘
Likbenta trianglar
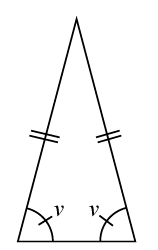
I en likbent triangel är två sidor lika långa. Detta medför att basvinklarna i en liksidig triangel är lika stora.
Exempel 2
Bestäm storleken av vinkeln vv i den likbenta triangeln.
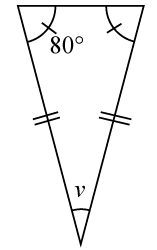
Lösning
Triangeln är likbent så basvinklarna är lika stora. I det här fallet är basvinklarna längst upp och de är bägge 80∘80∘.
Vi får då
v=180∘−80∘−80∘=20∘v=180∘−80∘−80∘=20∘
Liksidiga trianglar
I en liksidig triangel är alla sidor lika långa. I en sådan triangel gäller att alla vinklar är lika stora. Då 3180∘180∘3 =60∘=60∘ så gäller att alla vinklar är 60∘60∘.
Vad är höjden och basen i en triangel?
För att beräkna triangelns area behöver du veta längden på basen och höjden. Som vi tidigare nämnde i lektionen om triangeln och dess area, är det inte alltid helt enkelt att läsa av vilka längder i triangeln som motsvara dessa längder. Vi repeterar här kort vad som gäller.
En linje som är vinkelrät mot en annan kallas för en normal.
En triangels höjder är normaler dragna från en sida, eller en sidas förlängning, till motstående hörn. Höjderna skär varandra i en punkt.
Ett motstående hörn till en sida i en triangel, är det hörn som bildas mellan triangelns två andra sidor. Alltså det hörn som inte ”sitter fast” i något av basens ”slut”.
Genom att förlänga den sida man väljer till bas med en stödlinje, kan man rita ut höjden som en vinkelrät linje mellan det motstående hörnet och den ”förlängda” basen. Beroende på vilken sida du väljer som bas kommer höjden förändras.
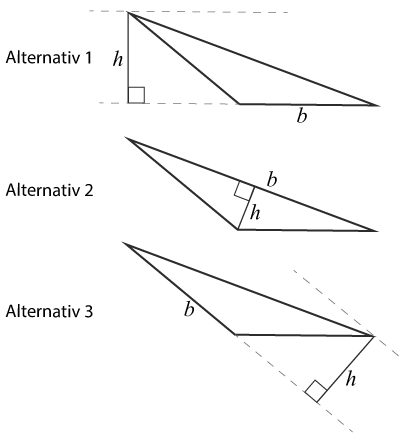
Triangelns höjd motsvarar alltså alltid det vinkelräta avståndet mellan basen och det motstående hörnet i triangeln.
Exempel i videon
- Bestäm storleken av vinkeln v i en likbent triangel.
- Vinkeln a är 25 % större än vinkeln b. Bestäm den rätvinkliga triangelns vinklar.
Kommentarer
e-uppgifter (5)
1.
(1/0/0)E C A B 1 P PL M R K Vilken typ av triangel är triangeln på bilden?
 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B 1 P PL M R K Vilken typ av triangel är det på bilden?
 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(2/0/0)E C A B 1 P 1 PL M R K Bestäm storleken av vinkeln vv i triangeln.
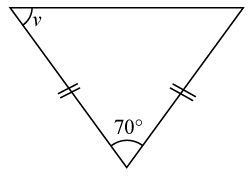 Svar:Ditt svar:Rätt svar: 55°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 55°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B 1 P PL M R K Är det något fel på triangelns vinklar?
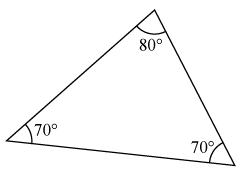 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B 1 P PL M R K Bestäm storleken av vinkeln vv.
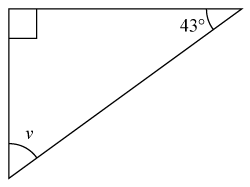 Svar:Ditt svar:Rätt svar: 47°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 47°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (1)
6. Premium
(0/1/0)E C A B P 1 PL M R K I en likbent triangel är basvinklarna fyra gånger så stora som den tredje vinkeln.
Bestäm storleken av den tredje vinkeln.
Svar:Ditt svar:Rätt svar: 20°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (1)
7. Premium
(0/0/1)E C A B P 1 PL M R K 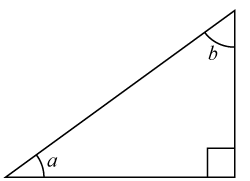
Vinkeln aa är 40 %40 % större än vinkeln bb. Bestäm storleken av vinkeln bb.
Svar:Ditt svar:Rätt svar: b=37,5°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Saeed Khadora
6 – I en likbent triangel är basvinklarna fyra gånger så stora som den tredje vinkeln. Bestäm storleken för av den tredje vinkeln.
är basvinklarna fyra gånger
Det betyder summan av basvinklarna är 4 gånger så stora . . . .
Annars måste fråga vara …. varje basvinkel är 4 gånger så stora ….
Svaret är 36 grader 72 + 72 andra vinklar
72+72 = 4 gånger 36
Ilse Hahne
Hej
Övning 7
Jag förstår inte steget b+ 1,4b= 2,4b
Simon Rybrand (Moderator)
Hej
Jag har skrivit ut fler steg i förklaringen till den uppgiften, kolla gärna lösningsförslaget där igen!
Evelina Malmros
I fråga 4 får man fel om man svarar att vinkelsumman är för stor, vilket ska vara rätt svar.
Anna Admin (Moderator)
Tack för ditt påpekande. Vi hade råkat missa att markera vilken fråga som var rätt. Nu är det korrigerat!
Jag Vet Inte
fel svar i facit fråga 4
Endast Premium-användare kan kommentera.