Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
I den här lektionen visar vi hur multiplikation fungerar med uppställning. Vi visar även en metod för att multiplicera tal med huvudräkning.
Räknesättet multiplikation
När två eller flera tal multipliceras med varandra så kallas detta för en multiplikation. Vid multiplikation spelar inte ordningen någon roll utan exempelvis gäller att 2⋅3=3⋅2. De tal man multiplicerar med varandra kallas för faktorer och resultatet av multiplikationen kallas för en produkt.
Exempel 1
Om vi beräknar 12⋅5=60 så kallas 12 och 5 för faktorer och 60 kallas för en produkt.
Vi kan lika väl skriva multiplikationen som 5⋅12=60
Multiplikation och huvudräkning
En metod för att multiplicera två tal med hjälp av huvudräkning är att dela upp det största talet i hundratal,
tiotal, ental, osv och multiplicera varje del med det mindre talet. Om talet är större delar du upp det med start i den största delen i talet.
Exempel 2
Beräkna 332⋅6 med hjälp av huvudräkning.
Lösning:
332⋅6=6⋅332
=6⋅300+6⋅30+6⋅2
=1800+180+12
=1980+12
=1992
Multiplikation med uppställning
Vid multiplikation med uppställning ställs talen upp ovanpå varandra på ett liknande vis som vid addition och subtraktion. Allmänt fungerar sedan metoden på följande vis.
- Ställ upp talen ovanpå varandra där du sätter det minsta talet underst.
- Multiplicera sedan den minsta typen av tal (tex entalen) i det nedersta talet med det minsta talet i det övre talet. Resultatet (produkten) av denna multiplikation sätts sedan under strecket.
- Om resultatet (produkten) av denna multiplikation är över 10 så skrivs tiotalet till höger som en minnessiffra och entalet under strecket. Minnessiffran adderas sedan till nästa multiplikation.
- Om det nedersta talet har fler än en siffra så görs metoden för varje siffra i det nedersta talet och sedan adderas resultaten (produkterna) till den slutgiltiga produkten.
Exempel 3
Beräkna 3⋅412 med uppställning.
Lösning:
Börja med att ställa upp talen ovanpå varandra där vi sätter det minsta talet 3 nederst.

Först multiplicerar vi 3⋅2=6 och sätter produkten nedanför strecket.
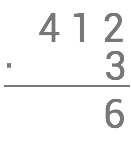
Nu multiplicerar vi 3⋅1=3 och sätter detta resultat nedanför strecket och till vänster om 6:an.
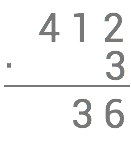
Slutligen multiplicerar vi 3⋅4=12 och sätter produkten längst till vänster nedanför strecket.
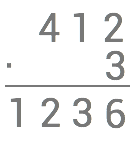
Här är alltså svaret 3⋅412=1236.
Exempel 4
Beräkna 781⋅7 med uppställning.
Lösning:
Vi börjar med att ställa upp talen ovanpå varandra och utför direkt den första multiplikationen med entalen där vi får 7⋅1=7.
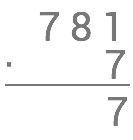
Nu multiplicerar vi 7⋅8=56 och här sätter vi tiotalssiffran 5 som en minnessiffra och entalssiffran 6 nedanför strecket.
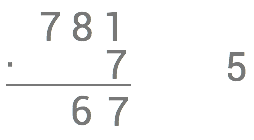
Nu multiplicerar vi 7⋅7=49 och adderar med vår minnessiffra så att vi får 49+5=54. Eftersom att vi inte har några mer multiplikationer att utföra sätter vi 54 under strecket längst till vänster.
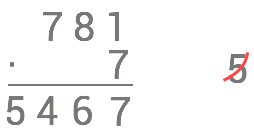
Här är alltså svaret att produkten är 781⋅7=5467
Exempel 5
Multiplicera 45⋅484 med uppställning.
Lösning:
Vi ställer först upp talen ovanpå varandra där det minsta talet är nederst.
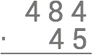
Nu multiplicerar vi 5⋅4=20 så vi sätter ut minnessiffran 2 och 0 nedanför strecket.
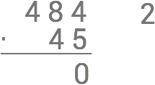
Nu multiplicerar vi 5⋅8=40 och adderar minnessiffran så att vi får 40+2=42. Vi sätter ut minnessiffran 4 och 2 nedanför strecket samtidigt som vi stryker över den förra minnessiffran.
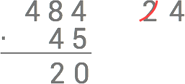
Nu multiplicerar vi 5⋅4=20 och adderar minnessiffran så att vi får 20+4=24 och stryker över den förra minnessiffran. Det är inga mer multiplikationer kvar för 5:an så vi sätter ut 24 längst till vänster.
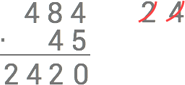
Nu fortsätter vi med 4:an i 45 och multiplicerar 4⋅4=16 och sätter ut 1 som minnessiffra och entalet 6 lodrätt nedanför 4:an i 45 och nedanför den första raden vi fick.
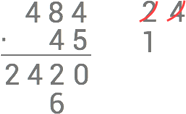
Nu multiplicerar vi 4⋅8=32 och adderar minnessiffran så att vi får 32+1=33 och stryker över den förra minnessiffran. Vi sätter ut minnessiffran 3 och 3 till vänster om 6:an.
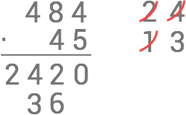
Nu multiplicerar vi 4⋅4=16 och adderar minnessiffran så att vi får 16+3=19 och stryker över den förra minnessiffran. Det är inga mer multiplikationer kvar för 4:an så vi sätter ut 19 längst till vänster.
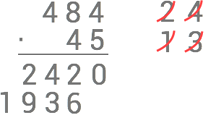
Slutligen så adderar vi de två raderna med varandra.
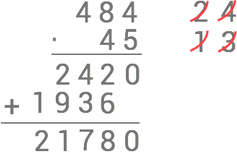
Här gäller alltså att produkten är 45⋅484=21780
Bra att kunna – Multiplikationstabellen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Exempel i videon
- Beräkna 224⋅6 med huvudräkning.
- Beräkna 112⋅3 med uppställning.
- Beräkna 432⋅8 med uppställning.
- Beräkna 612⋅31 med uppställning.
Kommentarer
e-uppgifter (8)
1.
Om du multiplicerar två tal, vad kallas då resultatet du får?
Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...2.
Om vi beräknar 5⋅4⋅3⋅2⋅1=120, vad kallas då talet 3?
Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...3.
Beräkna med hjälp av huvudräkning.
3⋅555
Svar:Ditt svar:Rätt svar: 1665(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
4. Premium
Beräkna med hjälp av huvudräkning.
12⋅1234
Svar:Ditt svar:Rätt svar: 14808(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
5. Premium
Beräkna med hjälp av uppställning.
3⋅911
Svar:Ditt svar:Rätt svar: 2733(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
6. Premium
Beräkna med hjälp av uppställning
5⋅556
Svar:Ditt svar:Rätt svar: 2780(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
7. Premium
Eva har utfört en multiplikation med uppställning på följande vis.
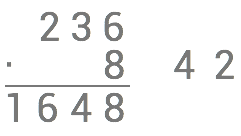
Avgör vilket av följande påståenden som stämmer.
Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...8. Premium
Beräkna med hjälp av uppställning
881⋅13
Svar:Ditt svar:Rätt svar: 11453(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Björn Melin
Nu skrev jag fel! Jag menar 5*2=16
Simon Rybrand (Moderator)
Tack! Vi ordnar det!
Björn Melin
Det står fel i Multiplikations tabellen. Bra att kunna – Multiplikationstabellen.
5*5=16
Endast Premium-användare kan kommentera.