Formelblad geometri - Geometriska figurer

Här samlar vi en mängd olika geometriska figurers grundläggande egenskaper som omkrets, area och volym. Du kan använda den här sidan som ett formelblad eller en referens när du jobbar med geometri.

Avståndet $d$d mellan två punkter $\left(x_1,\text{ }y_1\right)$(x₁, y₁) och $\left(x_2,\text{ }y_2\right)$(x₂, y₂) är

$d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$d=√(x₂−x₁)²+(y₂−y₁)²

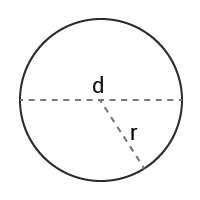
$Omkrets=\pi\cdot d=\pi\cdot2r$Omkrets=π·d=π·2r

$Area=\pi\cdot r^2=$Area=π·r²= $\frac{\pi\cdot d^2}{4}$π·d²4

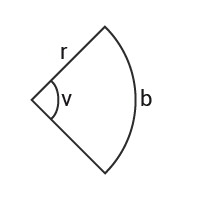
$B\text{å}gen\text{ }\text{ }b=$Bågen b= $\frac{v}{360^{\circ}}$v360^∘ $\cdot2\pi r$·2πr

$Area=$Area= $\frac{v}{360^{\circ}}$v360^∘ $\cdot\pi r^2$·πr² $=\frac{br}{2}$=br2

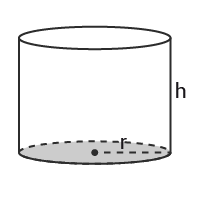
$Volym=\pi r^2h$Volym=πr²h

$Mantelarea=2\pi rh$Mantelarea=2πrh

I en kub är alla sidor lika långa.

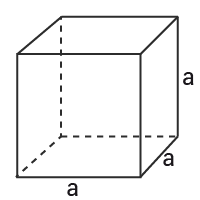
$Volym=a\cdot a\cdot a=a^3$Volym=a·a·a=a³

$Mantelarea=6\cdot a^2$Mantelarea=6·a²

I ett parallellogram är sidorna parvis lika långa och parallella.

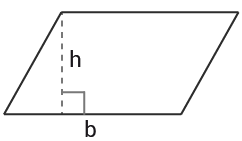
$Area=b\cdot h$Area=b·h

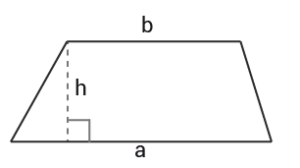
$Area=$Area= $\frac{h\left(a+b\right)}{2}$h(a+b)2

Talet π (Pi) beskriver förhållandet mellan en cirkels omkrets och diameter.

$\pi=\frac{Omkrets}{Diameter}$π=OmkretsDiameter

Vanligt är att talet avrundas till $\pi\approx3,14$π≈3,14

Den längsta sidan heter hypotenusan och är motstående till den räta vinkeln. De två andra sidorna heter katetrar.

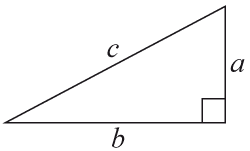
$a^2+b^2=c^2$a²+b²=c²

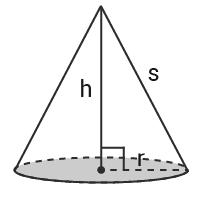
$Volym=$Volym= $\frac{\pi r^2h}{3}$πr²h3

$Mantelarea=\pi rs$Mantelarea=πrs

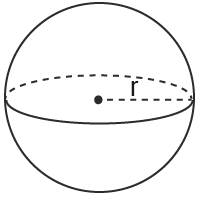
$Volym=$Volym= $\frac{4\pi r^3}{3}$4πr³3

$Area=4\pi r^2$Area=4πr²

Två geometriska figurer är likformiga om de har samma form, de kan dock ha olika storlek.

Två trianglar är likformiga om motsvarande trianglars vinklar är lika stora.

I en likformig triangel gäller också att förhållandet mellan motsvarande sidor i trianglarna detsamma.

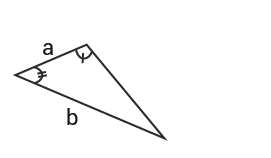
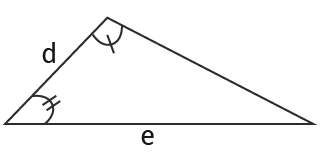
För de likformiga trianglarnas sidor gäller

$\frac{a}{d}=\frac{b}{e}$ad=be och $\frac{a}{b}=\frac{d}{e}$ab=de

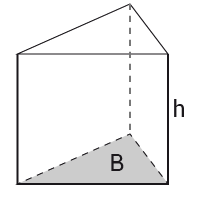
$Volym=B\cdot h$Volym=B·h där $B$B är basytans area.

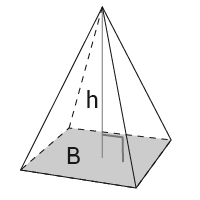
$Volym=$Volym=$\frac{Bh}{3}$Bh3

Då en randvinkel och medelpunktevinkel tillhör samma cirkelbåge gäller att medelpunktsvinkel $u$u är dubbelt så stor som randvinkeln $v$v.

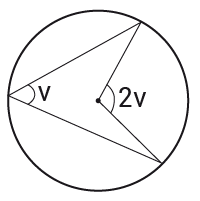
$u=2v$u=2v

$Area=a\cdot b$Area=a·b

$Omkrets=2a+2b$Omkrets=2a+2b

En romb är ett specialfall av en parallellogram. För en romb gäller att alla sidor $a$a är lika långa, och sidorna parvis parallella.

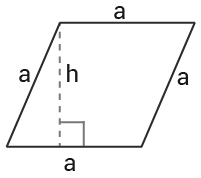
$Area=a\cdot h$Area=a·h

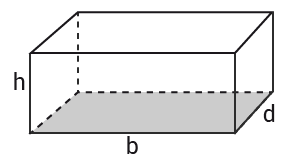
$Volym=b\cdot d\cdot h$Volym=b·d·h

$\text{Areaskala}=\left(\text{Längdskala}\right)^2$Areaskala=(Längdskala)²

$\text{Volymskala}=\left(\text{Längdskala}\right)^3$Volymskala=(Längdskala)³

Höjden $h$h är alltid vinkelrät mot basen $b$b.

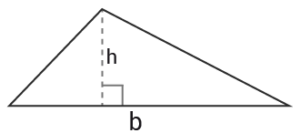
$Area=$Area= $\frac{bh}{2}$bh2