Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
I denna lektion fördjupar vi kunskaperna i hur du löser andragradsekvationer. Vi kommer titta närmre på andragradsekvationer som är skrivna på lite annorlunda form jämfört med pq-formeln i formelbladet.

Vi repeterar lösningsformeln, även kallad PQ-formeln.
Lösningsformeln
Andragradsekvationen $x^2+px+q=0$x2+px+q=0 har lösningarna
$x_{1,2}=$x1,2= $-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$−p2 ±√(p2 )2−q
Nödvändigt förarbete
För att kunna använda PQ – formeln så måste andragradsekvationen skrivas om på formeln x2+px+q=0x2+px+q=0
Det innebär att a=1a=1 och det ena ledet måste vara lika med noll. Först då kan vi tillämpa denna formel.
Två nödvändiga check
Koefficienten framför andragradstermen måste vara lika med ett.
Ena ledet måste vara lika med noll.
Om andragradsekvationen inte är lika med noll
En andragradsekvation kan behöva skrivas om innan man kan använda lösningsformeln. Den måste nämligen så på en sådan form att andragradstermens koefficient är lika med ett och att ett av leden är lika med noll. Vi tar ett exempel.
Exempel 1
Lös andragradsekvationen 24x=27−3x224x=27−3x2
Lösning
Vi börjar med att subtrahera båda leden med 24x24x för att få noll i ena ledet
0=27−3x2−24x0=27−3x2−24x
Nu dividerar vi med −3−3 för att få koefficienten framför andragradstermen lika med ett
0=x2+8x−90=x2+8x−9
Nu står ekvationen på rätt form och vi kan använda oss av pq-formeln för att lösa ut de bägge rötterna.
x=x= −28±(28)2−(−9)−82 ±√(82 )2−(−9)
x=−4±42+9x=−4±√42+9
x=−4±16+9x=−4±√16+9
x=−4±25x=−4±√25
x=−4±5x=−4±5
{x1=1x2=−9
Diskriminant
I kommande genomgångar kommer vi studera grafer till andragradspolynom. Hur dessa ser ut kommer bland annat påverkas av värdet under rottecknet i pq-formeln. För att lättare kunna förklara olika skeenden är det därför bra att känna till att (2p)2−q(p2 )2−q kallas för ekvationens diskriminant.
Värdet på diskriminanten kommer avgöra hur många reella lösningar som andragradsekvationen har. Men mer om det i lektionen om andragradsfunktionens nollställen.
Om diskriminanten har värdet noll, det vill säga (2p)2=q(p2 )2=q kommer ekvationen får en så kallad dubbelrot. Det innebär att andragradsekvationens nollställen är lika med varandra, x1=x2x1=x2
Exempel 2
Lös andragradsekvationen 2x2+18=−12x2x2+18=−12x
Lösning
Vi börjar med att skriv om ekvationen för PQ-formeln.
2x2+18=−12x2x2+18=−12x addera båda led med 12x12x för att få noll i ena ledet
2x2+12x+18=02x2+12x+18=0 dividerar vi med 22 för att få koefficienten framför andragradstermen lika med ett
x2+6x+9=0x2+6x+9=0
Nu står ekvationen på rätt form och vi kan använda oss av pq-formeln för att lösa ut de bägge rötterna x1x1och x2x2.
x=x= −26±(26)2−9−62 ±√(62 )2−9
x=−3±32−9x=−3±√32−9
x=−3±9−9x=−3±√9−9
x=−3±0x=−3±√0
x=−3±0x=−3±0
{x1=−3x2=−3
Ekvationen har en dubbelrot eftersom att x1=x2x1=x2 .
Det innebär att det är bara ett värde på xx som uppfyller likheten mellan VL och HL. I detta fall har ekvationen bara ett nollställe. I lektionen om symmetrilinjen och nollställen kommer vi titta närmre på hur detta visar sig i grafen till andragradsfunktionen.
abc-formeln
I stora delar av världen använder man abc-formeln i stället för pq. Fördelen med den är att vi inte behöver skriva om ekvationen med koefficienten 11 framför andragradstermen innan vi tillämpar formeln utan kan sätta in värden direkt från alla andragradsekvationer.
abc-formeln
Andragradsekvationen ax2+bx+c=0ax2+bx+c=0 har lösningarna
x1,2=x1,2= 2a−b±b2−4ac−b±√b2−4ac2a
Det vill säga de två lösningarna ges av
x1=x1= 2a−b+b2−4ac−b+√b2−4ac2a och x2=x2= 2a−b−b2−4ac−b−√b2−4ac2a
Exempel 3
Lös andragradsekvationen 2x2+4x−6=02x2+4x−6=0
Lösning
Vi läser av a=2a=2 , b=4b=4 och c=−6c=−6 och sätter in i acb-formeln för att lösa ut de bägge rötterna x1x1och x2x2.
x1,2=x1,2= 2⋅2−4±42−4⋅2⋅(−6)−4±√42−4·2·(−6)2·2
x1,2=x1,2= 4−4±16+48−4±√16+484
x1,2=x1,2= 4−4±64−4±√644
x1,2=x1,2= 4−4±8−4±84
x1,2=x1,2= 4−4±28−44 ±82
x1,2=−1±2x1,2=−1±2
{x1=1x2=−3
När det gäller att lösa andragradsekvationer är det oftare lättare huvudräkning med pq-formeln. Men när det gäller att hitta samband mellan symmetrilinjen, nollställen och grafens utseende kan det underlätta med abc-formeln.
PQ-formeln och tredjegradsekvationer
I matematik 2 krävs det inte att du skall kunna lösa alla tredjegradsekvationer. Men genom att använda de kunskaper vi har i faktorisering i kombination med nollproduktmetoden, kvadratrotsmetoden och lösningsformen kan vi lösa ekvationer som till en början ser riktigt besvärliga ut. Vi tar två exempel här.
Exempel 4
Lös tredjegradsekvationen x3+4x2=5xx3+4x2=5x
Lösning
Vi börjar med att subtrahera med i 5x5x båda leden
x3+4x2−5x=0x3+4x2−5x=0
Nu bryter vi ut xx ur varje term.
x(x2+4x−5)=0x(x2+4x−5)=0
Enligt nollproduktmetoden så kan vi här se att vi har en lösning x1=0x1=0. De andra två lösningarna får vi om vi löser ekvationen i parentesen.
x2+4x−5=0x2+4x−5=0
x2,3=x2,3= −24±(24)2−(−5)−42 ±√(42 )2−(−5)
x2,3=−2±22+5x2,3=−2±√22+5
x2,3=−2±4+5=−2±3x2,3=−2±√4+5=−2±3
x2,3=−2±3x2,3=−2±3
{ x2=−2−3=−5x3=−2+3=1
Ekvationens tre lösningar är därmed
⎩⎪⎪⎨⎪⎪⎧x1=0x2=−5x3=1
I detta fall har vi alltså tre olika värden på xx som ger att likheten mellan VL och HL stämmer.
Exempel i videon
- Lös ekvationen 3x2–39+36x=0.
- Lös ekvationen 8x2–54=48x+2x2.
- Lös ekvationen x2+2x–163=0
Kommentarer
e-uppgifter (8)
1.
(1/0/0)E C A B P PL M R 1 K 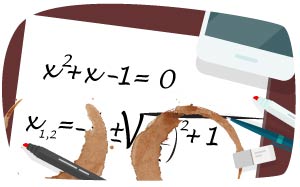
Ännu en olycka! Hjälp din vän att ange vad som ska stå under kaffefläcken.
Svar:Ditt svar:Rätt svar: 21(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: PQ – formelnRättar...2.
(1/0/0)E C A B 1 P PL M R K Vilken metod är mest lämplig för att lösa ekvationen x2−10x=10x2−10x=10 ?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)E C A B P 1 PL M R K Lös ekvationen x2+3=−4xx2+3=−4x
Svar:Ditt svar:Rätt svar: x1=−1 och x2=−3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: PQ – formelnRättar...4. Premium
(2/0/0)E C A B P 2 PL M R K Lös andragradsekvationen 51=54x−3x251=54x−3x2
Svar:Ditt svar:Rätt svar: {x1=17x2=1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(2/0/0)E C A B P 2 PL M R K Lös ekvationen 4x2+16x+12=04x2+16x+12=0
Svar:Ditt svar:Rätt svar: x1=−3 och x2=−1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(2/0/0)E C A B P 2 PL M R K Lös andragradsekvationen 2x2+32=−16x2x2+32=−16x
Svar:Ditt svar:Rätt svar: {x1=−4x2=−4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: PQ – formelnRättar...7. Premium
(1/0/0)ME C A B P 1 PL M R K Lös ekvationen −30+x2=114−30+x2=114
Svar:Ditt svar:Rätt svar: x=±12(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(1/0/0)ME C A B P 1 PL M R K Lös ekvationen 10x2+80x−650=010x2+80x−650=0
Svar:Ditt svar:Rätt svar: {x1=5x2=−13(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (4)
9. Premium
(0/2/0)E C A B P 2 PL M R K Lös andragradsekvationen
3x2−3x+121=x23 −x3 +112 = 00
Svar:Ditt svar:Rätt svar: {x1=21x2=21(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: PQ – formelnRättar...10. Premium
(0/2/0)E C A B P 2 PL M R K Lös andragradsekvationen
x2−x2− 54x−51=4x5 −15 = 00
Svar:Ditt svar:Rätt svar: {x1=1x2=−51(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: PQ – formelnRättar...11. Premium
(1/1/0)E C A B P 1 1 PL M R K Lös andragradsekvationen x2+365=xx2+536 =x
Svar:Ditt svar:Rätt svar: x1=65 och x2=61(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...12. Premium
(0/2/0)M NPE C A B P 2 PL M R K Lös ekvationen 3x2−4x−29=2x+163x2−4x−29=2x+16 med algebraisk metod.
Svar:Ditt svar:Rätt svar: x1=−3 och x2=5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Träna mera på PQ-formelnRättar...
a-uppgifter (2)
13. Premium
(0/0/1)M NPE C A B P PL 1 M R K Lös ekvationen (x−3)2−4(x−3)+3=0(x−√3)2−4(x−√3)+3=0 om du vet att t2−4t+3=0t2−4t+3=0 har lösningarna t1=3t1=3 och t2=1t2=1. Svara med exakta värden.
Svar:Ditt svar:Rätt svar: x1=3+3 och x2=1+3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...14. Premium
(0/0/3)M NPE C A B P 1 PL M R 2 K I ekvationen ax2−a2x=−2ax2−a2x=−2 är aa en positiv konstant. Lös ekvationen och visa vilka värden på aa som ger två olika reella rötter.
Svar:Ditt svar:Rätt svar: a>2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Träna mera på PQ-formelnRättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Alexandra Goicoechea
I fråga 12 så förstår inte jag frågan. Det finns två formler och det verkar som att jag ska dra slutsatser om en formel från den andra. Men de har ju inte samma variabler. Vad är frågan egentligen?
arre
hej, är inte svaret på exempel 3 i videon att x = -1/4 (+-) roten ur roten ur 7 / roten ur 32..
det känns som att du missar att dividera 3/16 med 2/1 eller har jag fel.. för jag gjorde så på -1/2 och fick det till -1/4 och sen samma sak med 3/16.. kolla gärna videon och så förstår du nog vad jag yrar om…
Simon Rybrand (Moderator)
Hej!
Där skall vi inte dividera 3/16 med något alls. Vi behöver inte dela eller multiplicera med någon innan vi tillämpar pq-formeln. Däremot så är det ju en hel del att hålla reda på med bråktalen och roten ur där 😉
Erik Åblad
Hej!
I fråga 3 står att man ska fylla i vad som står i ”den tomma rutan”. Det är två tomma rutor, säkerligen uppenbart för de flesta men kanske bör ändras till: de två tomma rutorna.
mvh
Hugo Elfner
Hej, på uppgift 5 får jag fram svaret -1 och -3 istället för 1 och 3,
hur kommer det sig?
Båda jag och flera vänner har fått samma svar och vi vet inte varför svaret är positivt, gör vi något fel eller är det fel på frågan? Tack mvh Hugo
Simon Rybrand (Moderator)
Det var fel på frågan och det är korrigerat nu, tack för att du sade till.
Endast Premium-användare kan kommentera.