Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
I den här lektionen lär du dig att använda additionsmetoden för att lösa linjära ekvationssystem.
Additionsmetoden är en algebraisk metod för att lösa linjära ekvationssystem. Det innebär att du med metoden kan lösa en ekvations med mer än en okända variabler.
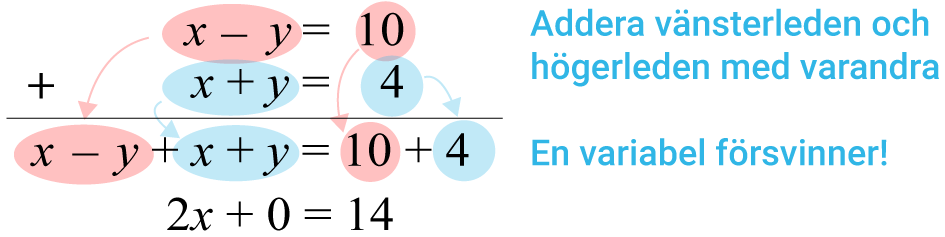
Metoden går ut på att du genom att skriva om och sedan adderar de två ekvationerna får en variabel att elimineras (försvinna). Detta gör att du går från en ekvation med två variabler till en. Du kan på detta vis få fram hela lösningen.
Så fungerar additionsmetoden
Ofta kan man behöva multiplicera ena eller båda ekvationerna innan du utför additionen för eliminering. Detta för att koefficienterna framför en av variablerna ska bli motsatta tal.
Additionsmetoden
När du löser linjära ekvationssystem med additionsmetoden gör du på följande vis.
- Undersök om någon av koefficienterna till ena variabeln i de två ekvationerna är motsatta tal. Exempelvis är 22 och −2−2 motsatta tal. Dessa två kommer att bli lika med noll (elimineras) om de adderas.
- Om inte någon av variablernas koefficienter är motsatta tal skriver du om ena eller båda ekvationerna för att uppnå det.
- Addera båda ekvationerna ledvis. Ena variabeln elimineras (försvinner).
- Bestäm variabelns värde i den ekvation som skapas och som nu bara har en variabel.
- Använd din lösning och bestäm värdet på den andra variabeln genom att sätta in den första variabelns värde i någon av de ursprungliga ekvationerna.
- Ange ekvationssystemets lösning genom att sammanbinda de två variablernas värde med en klammer.
Principen bakom additionsmetoden
Nedan visas i en animation principen bakom additionsmetoden. Animationen visar hur balansen mellan vänsterledet och högerledet kvarstår när de bägge ekvationerna adderas.

Räkneexempel
Exempel 1 – Addera direkt
Använd additionsmetoden och lös ekvationssystemet
{y+x=4(1)6x−y=3(2)
Lösning
Här ser vi att en av variablerna, yy, har koefficienter som är motsatta tal. Det gör att termerna yy och −y−y i ekvationerna kommer att få summan noll/”ta ut varandra”. Vi kan därför addera dem direkt och eliminerar då en variabel.
Addera båda ekvationerna ledvis.
x+y=4x+y=4
+ 6x−y=3+ 6x−y=3
____________________
7x+0=77x+0=7
Lös ekvationen
7x=77x=7 dividera båda led med 77
x=1x=1
Bestäm yy genom att sätta in x=1x=1 i ekvation (1).
y+1=4y+1=4 subtrahera båda led med 11
y=3y=3
Ekvationssystemets lösning är {x=1y=3
Exempel 2 – Multiplicera först, sedan addera
Använd additionsmetoden och lös ekvationssystemet
{y−x=1(1)3y+6x=21(2)
Lösning
I det här ekvationssystemet har vi inga motsatta tal/termer. Så om vi adderar direkt så kommer ingen variabel att elimineras. Det vi då kan göra är att multiplicera ekvation (1) med (−3)(−3) för att få termen (−3y)(−3y). Denna kommer då att eliminera 3y3y i ekvation (2).
När vi multiplicerar ekvation (1) med (−3)(−3) så gör vi det på följande vis.
{y⋅(−3)−x⋅(−3)=1⋅(−3)(1)3y+6x=21(2)
Vi adderar de båda ekvationerna ledvis.
−3y+3x=−3−3y+3x=−3
++ 3y+6x=21 3y+6x=21
___________________________________
−3y+3x+3y+6x=−3+21−3y+3x+3y+6x=−3+21 Förenkla
0+9y=180+9y=18
Lös ekvationen
9x=189x=18 dividera båda led med 99
x=2x=2
Bestäm yy genom att sätta in x=2x=2 i ekvation (1).
y−2=1y−2=1 addera båda led med 22
y=3y=3
Ekvationssystemets lösning är {x=2y=3
Exempel i videon
- Lös ekvationssystemet {x−y=10y+x=4 med additionsmetoden.
- Lös ekvationssystemet {y+3x=64x+2y=10 med additionsmetoden.
Kommentarer
e-uppgifter (8)
1.
(1/0/0)E C A B P 1 PL M R K 
Vilket tal ska du förlänga ekvation (1)(1) med för att eliminera xx -termerna om du använder additionsmetoden?
Svar:Ditt svar:Rätt svar: −2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(2/0/0)E C A B P 2 PL M R K Lös ekvationssystemet med additionsmetoden.
{2x+y=5x−y=1
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(2/0/0)E C A B P 2 PL M R K Lös ekvationssystemet med additionsmetoden.
{3x+y=4−3x+2y=−10
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(2/0/0)E C A B P 1 PL M R 1 K Kim har löst ekvationssystemet med hjälp av additionsmetoden.
Studera lösningen och välj det påstående du tycker stämmer bäst. Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)E C A B 1 P PL M R K Vilket tal ska du förlänga ekvation (1)(1) med för att eliminera yy-termerna om du använder additionsmetoden?
{2y=x+4(1)−8y+6=x (2)
Svar:Ditt svar:Rätt svar: 4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(2/0/0)M NPE C A B P 2 PL M R K Lös ekvationssystemet {2x+y=66x−2y=28
Svar:Ditt svar:Rätt svar: {x=4 y=−2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(2/0/0)ME C A B P 2 PL M R K Lös ekvationssystemet med additionsmetoden.
{x+y=42x−3y=−7
Svar:Ditt svar:Rätt svar: {x=1y=3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(2/0/0)ME C A B P 2 PL M R K Lös ekvationssystemet med additionsmetoden.
{2x−8y+12=0x−12y+8=0
Svar:Ditt svar:Rätt svar: {x=−5y=41(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (2)
9. Premium
(0/2/0)M NPE C A B P 2 PL M R K Lös ekvationssystemet algebraiskt
{(x+4)(y−2)=(x−5)(y+4)6y−x−6=2x−y−2
Svar:Ditt svar:Rätt svar: {x=8y=4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(0/1/0)E C A B P PL M R 1 K Bestäm kk så att xx-termerna elimineras när du använder additionsmetoden, utan att du behöver förlänga eller förkorta någon av ekvationerna.
{y=kx+mf(x)=ax+b
Svar:Ditt svar:Rätt svar: k=−a(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Noah Juma
Hej, fråga 6.
Ni har svarat (x=-2 och y=-5) det är fel, det ska vara (x=-4 och y=-11)
Hanna Nilsson
Hej!
Hur löser jag detta ekvationssystem med hjälp av additionsmetoden?
2x-y=3 (1)
15-2x=3y (2)
MVH Hanna
Simon Rybrand (Moderator)
I ekvation (1) har du termen +2x och i ekvation (2) har du termen -2x. Dessa två termer tar ut varandra när du adderar ekvationerna:
2x-y=3
15-2x=3y
Addition ger
2x-y+15-2x=3+3y
-y+15=3+3y
Nu har du bara en okänd variabel kvar!
David Ygge
På uppg. 7 så borde väl även -4 vara ett korrekt svar, man behöver ju faktiskt inte flytta om bland termerna för att eliminera y-termen:
-8y = -4x – 16 och 6 = x +8y ger genom additionsmetoden x = -4x – 10
Eller?
Mvh David
Simon Rybrand (Moderator)
Hej, helt rätt. Du kan utföra elimineringen efter multiplikationen också.
Vi korrigerar uppgiften.
Berkan991
som t.ex
5x-2y=7
7x+6y=45
Simon Rybrand (Moderator)
Ja där får du multiplicera ena eller bägge ekvationerna med något tal så att någon av variablerna tar ut varandra. Här är det enklast att multiplicera den översta ekvationen med 3 så att du får −6y där. Sedan addera dem. Det kan se ut så här:
5x−2y=7Multiplicera med 3
7x+6y=45
——————
15x−6y=21
7x+6y=45
——————
Vid addition av ekvationerna får du
22x=66
x=3
——————
Sedan blir det enkelt att lösa ut y
Berkan991
Hej!
Om en ekvation inte ha termer som inte tar ut varandra, ska man då multiplicera så att termerna kan ta ut varandra? Är det bara när man inte kan ta ut varandra man ska multiplicera?
Simon Rybrand (Moderator)
Hej
Har du ett exempel som vi kan utgå ifrån? Det blir lättare att förklara då.
Simon Rybrand (Moderator)
Hej
Ett sätt (det finns flera vägar till lösningen) är att multiplicera den första ekvationen med −3 och en andra med 2 vilket ger ekvationssystemet
-6x-12y=-177
6x+6y=126
När ekvationerna adderas med varandra elimineras variabeln x och vi får ekvationen
-6y=-51
y=8,5
Sedan kan du lösa ut x.
Komvux Sundsvall Elev
Hej! Jag skulle verkligen behöva hjälp med att lösa ut:
2x+4y=59
3x+3y=63
Jag har försökt att lösa ut talet genom förklaringen i boken men det blir bara fel och i mathleaks står det att man ska dividera den andra ekvationen med 3 och sedan multiplicera med (-4).. Blir bara helt förvirrad och vet inte längre hur jag ska göra! Tacksam för svar 🙂
Komvux Sundsvall Elev
Hej! Hur löser man
2x+4y =59
3x+3y =63
Jag har försökt att lösa talet genom förklaringarna i boken men det blir bara fel och i mathleaks står det att man ska dividera bort den andra ekvationen med 3 och sedan multiplicera med (-4).. J
nadja.pavlova.rashid92@gmail.com
Hej, jag undrar hur man bör tänka när man löser denna uppgift med hjälp av substitutionsmetoden…
4x+y= -9
6x=2y+4
Simon Rybrand (Moderator)
Hej
Det kan vara lämpligt att lösa ut y i den översta ekvationen då du inte har någon koefficient (något tal) framför variabeln y.
Du får då att
y=−9−4x
Detta sätter du nu in (substituerar) i den andra ekvationen så att du får
6x=2(−9−4x)+4⇔
6x=−18−8x+4⇔
14x=−14⇔
x=−1
Sedan använder du detta för att lösa ut y
veritas87
2x + 3y = -6
3x – 4y = 25
= 5x + y = 19
Och hur räknar jag sedan? Har jag räknat rätt här ovan?
Tacksam för svar!
Simon Rybrand (Moderator)
Innan du adderar de bägge ekvationerna behöver du multiplicera dem med något så att du eliminerar en variabel. Du skulle kunna multiplicera den översta med 3 och den nedersta med (-2) får du:
6x+9y=-18
-6x+8y=-50
När du nu adderar de bägge ekvationerna så kommer variabeln x att elimineras, du får alltså ekvationen
17y=68
y=4
Sedan behöver du bara lösa ut x.
maggie liew
ok, det ska jag göra, tusen tack för ditt snabbt svar.
mvh
Maggie
David Granlund
Hej, hur räknar jag ut (1) y=2x+2 (2) y=x-2 med hjälp av additionsmetoden, jag får ut fel svar och vet inte vad jag gör fel. 🙁
Simon Rybrand (Moderator)
{y=2x+2(1)y=x−2(2)
Multiplicera ekvation (1) med (-1)
{−y=−2x−2(1)y=x−2(2)
Addera ekvationerna med varandra sa˚ att y elimineras
−y=(−2)x−2
+y=x−2
———————
0=−x−4⇔
x=−4
Vi sätter in detta i någon av ekvationerna och får att y=−6
Hjälper detta dig att se hur du kan använda additionsmetoden för att lösa detta ekvationssystem?
jesibra
hej! har du ingen video på hur man använder substitionsmetoden? eller är substitutionmetoden och additionsmetoden samma sak?
Mvh jesibra
Simon Rybrand (Moderator)
Hej, jo det finns, du hittar den här:
/lektioner/linjara-ekvationssystem/
tobias peterson
Den verkar inte finnas kvar? Hittar ingen video alls om sub-metoden, har den raderats?
Simon Rybrand (Moderator)
Hej
Kolla här: /lektioner/linjara-ekvationssystem/
Länken var felaktig
lovisa
Hej!!
Har problem här:
2x-8y+12=0
x-12y+8=0
Jag har försökt multiplicera in -2 i ekvation 2 men får inte rätt på det!
Simon Rybrand (Moderator)
Tycker att det verkar vara en bra idé att multiplicera in -2 i ekvation 2:
2x-8y+12=0
-2x+24y-16=0
Addera så ges ekvationen
16y-4=0
y=1/4
Lös sedan ut x.
Ulrica Pinones Gunnarsson
Hej,
Jag har fastnat, säkert jätte enkelt.
Hur löser man denna?
X+Y=6
Y=3X-2
MVH Ulrica
Simon Rybrand (Moderator)
(1) x+y=6
(2) y=3x-2
Från ekvation (1) kan du lösa ut x = 6 – y
Substituera nu x i ekvation (2) mot 6 – y:
y=3(6-y)-2 ⇔
y = 18 – 3y – 2 ⇔
y = 16 – 3y ⇔
4y = 16
y = 4
Vi kan nu ta fram x genom att sätt in y i (1) vilket ger x = 6 – 4 = 2
Alltså:
x = 2
y = 4
melker
hej!
jag jobbar med ekvationssystem
kan du lösa detta
3x+6y=178,50
8x+2y=168
och förklara hur du gjorde?
mvh
Simon Rybrand (Moderator)
Hej, här kan du använda additionsmetoden och det är lämpligt att förlänga den andra ekvationen med (-3) så att du kan eliminera y. Vi får då
3x+6y=178,50
-24x-6y=-504
Nu adderar vi dessa ekvationer:
3x+6y=178,50
-24x-6y=-504 +
————————
-21x = -325.5 (dividera med -21)
x = 15,5
Nu har vi x och kan lösa ut y och får då att y = 22.
juliasofi
Hej.
I uppgift 4 får jag x = -5 och y = 1/4. När jag sätter in 1/4 i en av lösningarna får jag 2x-(8*1/4)+12=0 -> 2x-2+12=0 -> 2x+10=0 -> 2x=-10 -> x=-5. Vad gör jag för fel?
Med vänlig hälsning, Julia
Simon Rybrand (Moderator)
Hej! Nej du gör inte fel där utan det är ett tecken som fattas i de sista uträkningarna i uppgiften och det skall vara -5, tack för att du påpekade det, vi har korrigerat testet.
johansson50
Hej, hur gör jag med dessa? Kan inte riktigt få fram vilket tal det är jag ska multiplicera med.
3x – y + 7 = 0
x + 2y – 7 = 0
2x – 3y – 5 = 0
3x – 5y – 9 = 0
Finns det någon regel som säger vad det är man får multiplicera talen med eller gäller det enbart att hitta gemensam nämnare så att y tar ut varandra?
Sedan undrar jag också vad det är som avgör vilket led man ska multiplicera in x-värdet i för att få ut Y ?
Mvh/
Camilla
Simon Rybrand (Moderator)
Hej Camilla, målet är att eliminera en av variablerna genom att multiplicera med ett tal innan ekvationerna adderas med varandra. Så om du siktar på att eliminera x eller y spelar egentligen ingen roll utan man försöker göra det så smidigt som möjligt. Tex i det exemplet du nämner:
3x – y + 7 = 0
x + 2y – 7 = 0
Här ser det smidigt ut att multiplicera den övre ekvationen med 2 för att då får vi -2y där. Denna term kommer då att eliminera +2y i den andra ekvationen, dvs -2y + 2y = 0. Sedan har du bara en variabel kvar som du löser ut.
När du väl har fått fram en variabels värde, t.ex. x, så sätter du in detta värde i någon av ekvationerna. Då kommer du kunna att lösa ut den andra variabeln.
scaleo
Hej , hur löser man :
en rätt linje går genom (-3,5) och (a,2). den skär x axeln i punkten x=7. Bestäm a
Simon Rybrand (Moderator)
Hej eftersom du vet att den skär x – axeln i (7, 0) kan du använda detta tillsammans med punkten (-3, 5) för att ta reda på lutningen och m – värdet. Sedan sätter du in (a, 2) i den ekvation du får fram och kan på det viset ta fram värdet på a.
annab87
Hur tänker man när det gäller denna=/
3x+2y-5=0
2y-3x+7=0
mvh
Simon Rybrand (Moderator)
Hej, eftersom du har +3x i den första ekvationen och -3x i den andra ekvationen så kommer denna variabel att elimineras när du adderar de bägge ekvationerna enligt:
3x+2y-5=0
+ 2y-3x+7=0
—————–
4y + 2 = 0
y = (-1/2)
Sedan använder du detta svar för att lösa ut x
annab87
okej, tack tack!
minerva
Mycket bra genomgång!
JacobHP
tack för snabbt och bra svar. Jag glömde bara byta tecken när jag flyttade över Y:et..
slarv..
JacobHP
hej. varför blir svaret fel om man använder substitionsmetoden på samma uppgift? jag trodde det fungerade, bara att additionsmetoden fungerade bättre i detta fall. Antigen räknar jag fel, men jag får ett annat svar. på uppgiften x-y = 10 och 3x +y = 2
Simon Rybrand (Moderator)
Hej Jakob, det stämmer att du skall kunna få samma svar med hjälp av substitutionsmetoden på samma ekvationssystem. Du skulle kunna ställa upp och lösa det med substitionsmetoden såhär:
(1) x – y = 10 => x = 10 + y
(2) 3x + y = 2
——————
(1) i (2) ger att
3(10 + y) + y = 2 <->
30 + 3y + y = 2 <->
30 + 4y = 2 <->
4y = -28 <->
y = -7
——————-
(2) insatt i (1) ger att
x – (-7) = 10 <->
x = 3
En något längre uträkning här alltså 😉
Endast Premium-användare kan kommentera.