Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 2b
/ Andragradsfunktioner
Hitta symmetrilinjen - alternativ metod
I den här lektionen visar vi hur vi kan hitta symmetrilinjen med en alternativ metod som gör arbetet med att hitta symmetrilinjen utifrån funktionsuttrycket snabbare.
Symmetrilinjens ekvation
I den här lektionen visar vi hur vi snabbt kan ta fram symmetrilinjens ekvation genom att känna till följande samband.
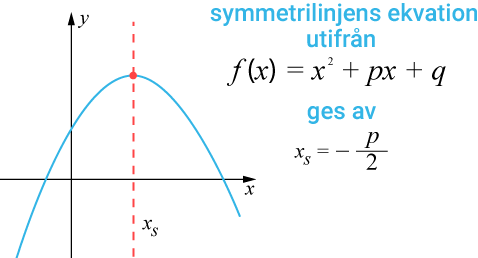
Symmetrilinjens ekvation
Om andragradsfunktionen står på formen
$f\left(x\right)=x^2+px+q$ƒ (x)=x2+px+q så är symmetrilinjens ekvation
$x_s=$xs= $-\frac{p}{2}$−p2
I en föregående lektion visar vi hur vi kan bestämma symmetrilinjens ekvation om vi har två $x$x-värden som har samma $y$-värde, exempelvis parabelns två nollställen. Den hittas då mitt emellan två punkter som har samma $y$y-värde. Eftersom dessa punkter har $x$x-koordinaterna $x_1$x1 och $x_2$x2 gäller att symmetrilinjens ekvation är
$x_s=$xs= $\frac{x_1+x_2}{2}$x1+x22
Denna metod fungerar lika bra att använda även om den vi går igenom i den här lektionen kan ses som "snabbare".
Exempel 1
Bestäm symmetrilinjens ekvation för följande andragradsfunktioner.
a) $f\left(x\right)=x^2+12x+2$ƒ (x)=x2+12x+2
b) $f\left(x\right)=10x^2+7$ƒ (x)=10x2+7
c) $f\left(x\right)=3x^2-2x+12$ƒ (x)=3x2−2x+12
Lösning
a) Här gäller att $p=12$p=12 och därmed är symmetrilinjens ekvation
$x_s=$xs= $-\frac{p}{2}=-\frac{12}{2}=$−p2 =−122 =$-6$−6
b) Här gäller att $p=0$p=0 eftersom vi saknar en förstagradsterm.
$x_s=$xs= $-\frac{p}{2}=-\frac{0}{2}=$−p2 =−02 = $0$0
Symmetrilinjen sammanfaller här med $y$y-axeln, dvs $x=0$x=0.
c) Här bryter vi först ut $3$3 för att få funktionsuttrycket i likhet med $pq$pq och kunna läsa av $p$p -värdet.
$f\left(x\right)=3x^2-2x+12$ƒ (x)=3x2−2x+12 bryt ut $3$3 i HL
$f\left(x\right)=3\left(x^2-\frac{2}{3}x+4\right)$ƒ (x)=3(x2−23 x+4)
Vi läser av att $p=$p=$-\frac{2}{3}$−23 och därmed är symmetrilinjens ekvation
$x_s=$xs=$-\frac{p}{2}=-\left(\frac{-\frac{2}{3}}{2}\right)=\frac{2}{6}=\frac{1}{3}$−p2 =−(−23 2 )=26 =13
abc-formeln
I stora delar av världen används abc-formeln i stället för pq-formeln. Fördelen med den är att vi inte behöver skriva om ekvationen med koefficienten $1$1 framför andragradstermen innan vi tillämpar formeln utan kan sätta in värden direkt från alla andragradsekvationer.
Då kan vi istället snabbt ta fram symmetrilinjens ekvation genom att känna till följande samband.
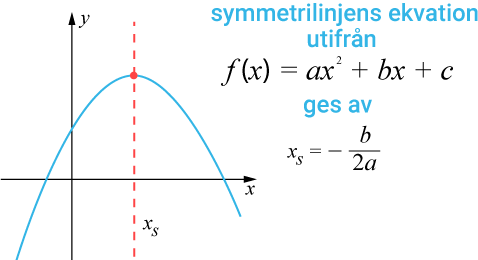
Symmetrilinjens ekvation
Om andragradsfunktionen står på formen
$f\left(x\right)=ax^2+bx+c$ƒ (x)=ax2+bx+c
så är symmetrilinjens ekvation
$x_s=$xs= $-\frac{b}{2a}$−b2a
Vi visar hur vi skulle lösa c)-uppgiften i exempel 1 med denna metod.
Exempel 2
Bestäm symmetrilinjens ekvation för andragradsfunktionen $f\left(x\right)=3x^2-2x+12$ƒ (x)=3x2−2x+12
Lösning
Vi kan alltså med detsamma läsa av $a=3$a=3 och $b=-2$b=−2 och få att
$x_s=$xs=$-\frac{b}{2a}=-\frac{-2}{2\cdot3}=\frac{1}{3}$−b2a =−−22·3 =13
Exempel i videon
- Härledning av metoden utifrån $f\left(x\right)=x^2+px+q$ƒ (x)=x2+px+q
- Bestäm symmetrilinjens ekvation om
a) $f\left(x\right)=x^2+2x+5$ƒ (x)=x2+2x+5
b) $f\left(x\right)=-9x^2+18x-4$ƒ (x)=−9x2+18x−4
c) $f\left(x\right)=x^2-22x$ƒ (x)=x2−22x
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (4)
-
1. Premium
Bestäm symmetrilinjens ekvation om $f\left(x\right)=x^2+4x+4$ƒ (x)=x2+4x+4
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...2. Premium
Bestäm symmetrilinjens ekvation om $f\left(x\right)=x^2-7x-12$ƒ (x)=x2−7x−12
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Andragradsfunktioner Hitta symmetrilinjen - alternativ metod Matematik 2 symmetrilinjeRättar...3. Premium
Ange symmetrilinjens ekvation om $f\left(x\right)=-56x^2$ƒ (x)=−56x2
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Andragradsfunktioner symmetrilinjeRättar...Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut!4. Premium
Ange symmetrilinjens ekvation om $f\left(x\right)=-3x^2-12x$ƒ (x)=−3x2−12x
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Andragradsfunktioner symmetrilinjeRättar...c-uppgifter (3)
-
5. Premium
Andragradsfunktionen $f\left(x\right)$ƒ (x) har nollställen $x_1=4-\sqrt{7}\text{ }$x1=4−√7 och $x_2=4+\sqrt{7}$x2=4+√7.
Bestäm symmetrilinjens ekvation.
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Andragradsfunktioner Hitta symmetrilinjen - alternativ metod Matematik 2 symmetrilinjeRättar...6. Premium
Ange symmetrilinjens ekvation om $f\left(x\right)=ax^2+bx+c$ƒ (x)=ax2+bx+c
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: symmetrilinje symmetrilinjens ekvationRättar...7. Premium
I koordinatsystemet är grafen till $f\left(x\right)=x^2+px$ƒ (x)=x2+px utritad.
Ange $p$p för den utritade funktionen.
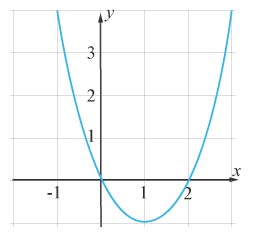Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Hitta symmetrilinjen - alternativ metodLiknande uppgifter: Andragradsfunktioner Hitta symmetrilinjen - alternativ metod symmetrilinjeRättar...a-uppgifter (1)
-
8. Premium
I koordinatsystemet är grafen till $f\left(x\right)=-x^2+bx-6$ƒ (x)=−x2+bx−6 utritad. Ange $b$b för den utritade funktionen.
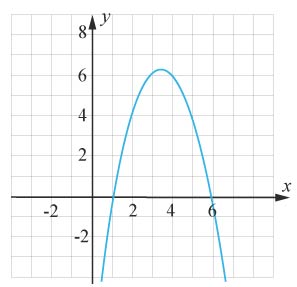Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Andragradsfunktioner Hitta symmetrilinjen - alternativ metod Matematik 2 symmetrilinjeRättar... -
-
Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut! -
Uppgiften är en del av en abc-fråga. Vad vill du göra?
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
Max Nordström
uppgift 8:
b är positiv, och för att få symetrilinjes x värde gör man xs=-p/x, alltså -b/2. grafens symetrilinje ligger på x=3,5, då blir ekvationen för b alltså 3,5=-b/2->7=-b->b=-7, eller missar jag något?
Eddler
Hej Max!
Formeln $x_s=-\frac{p}{2}$ gäller bara när koefficienten framför $x^2$ är $1$. Här står det $-x^2$, så vi dividerar först med $-1$ och får $x^2-bx+6$. Då är $p=-b$ och $x_s=\frac{b}{2}$.
Med $x_s=3{,}5$ blir $\frac{b}{2}=3{,}5$, alltså $b=7$.
Sarah Saidi
Jag förstår inte fråga 8, hur ser man att x1 är 3,5??
Aksel Nordin
I uppgift 8 står det i förklaringen att symmetrilinjens ekvation är x=-3,5. Men symmetrilinjens ekvation är väl ändå x=3,5? Alltså bör p-värdet vara -7,5; inte 7,5.
Samuel Gustafsson
Fråga 6 har fel svar. Man måste ju dividera med 9 först innan man plockar fram symmetrilinjen.
Endast Premium-användare kan kommentera.