Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
I den här lektionen fokuserar vi på att tillämpa linjära ekvationssystem och använda dem vid problemlösning. Följande lektioner är bra att ha gått igenom innan man tar sig an dessa uppgifter.
- Vad är linjära ekvationssystem
- Grafisk lösning av linjära ekvationssystem
- Substitutionsmetoden
- Additionsmetoden
Sammanfattningsvis gäller följande.
Ekvationssystemet har exakt en lösning då linjerna har en skärningspunkt.
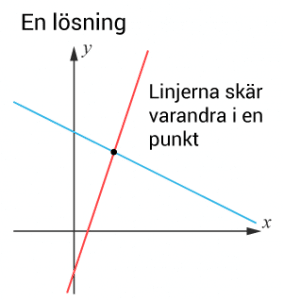
Det inträffar då linjernas lutning är olika. Med andra ord då k1=k2k1≠k2 .
Ekvationssystemet saknar lösning då linjerna saknar skärningspunkt.
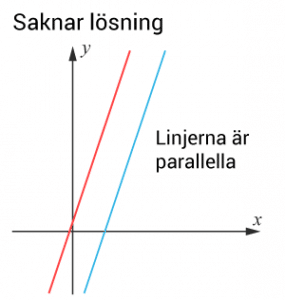
Det inträffar då linjernas lutning är lika, men har olika mm-värden. Med andra ord då k1=k2k1=k2 och m1=m2m1≠m2.
Ett linjärt ekvationssystem kan också ha oändligt antal lösningar. Det har ekvationssystemet om de bägge ekvationerna representerar samma linje.
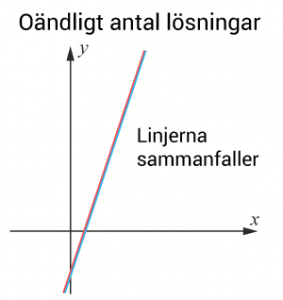
Alltså då k1=k2k1=k2 och m1=m2m1=m2.
Linjära ekvationssystem och problemuppgifter
När du löser textuppgifter där linjära ekvationssystem krävs för att kunna lösa dem, så är följande till väga gång bra.
- Använd informationen i textuppgiften för att ställa upp två ekvationer där samma två variabler används i ekvationerna.
- Ofta får du information om att två personer/längder/grupper osv har ett samband. Försök att tydliggöra dessa samband.
- Lös sedan det ekvationssystem du får fram med algebraisk metod.
Exempel 1

figur ej skalenlig
En rektangel har omkretsen 2424 cm. Den ena sidan är 22 cm längre än den andra. Kalla sidorna för aa och bb. Ställ upp ett ekvationssystem för aa och bb och lös det.
Lösning
Här kan vi använda de två sambanden som vi har fått information om.
Samband 1: Vi vet att omkretsen är 24 cm24 cm så då gäller att 2a+2b=242a+2b=24.
Samband 2: Den ena sidan är 2 cm2 cm längre än den andra, så då gäller att b=a+2b=a+2.
Nu ställer vi upp dessa bägge ekvationer i ett ekvationssystem
{2a+2b=24(1)b=a+2(2)
I ekvation (2) är redan variabel bb ensam, så vi sätter in den (substituerar) i ekvation (1)
2a+2b=242a+2b=24 Substituera
2a+2(a+2)=242a+2(a+2)=24 Förenkla VL
4a+4=244a+4=24 Subtrahera med 4
4a=204a=20 Dividera med 4
a=5a=5
Nu kan vi sätta in a=5a=5 i ekvation (2), vi får då
b=5+2=7b=5+2=7
Lösningen till ekvationssystemet är
{a=5b=7
Sidorna är alltså 5 cm5 cm och 7 cm7 cm
Exempel i videon
- På ett badhus har man en maxgräns på 86 personer som får vistas i bassängen samtidigt. En lördag förmiddag är det fullt i bassängen och i bassängen är det 4 kvinnor färre än halva antalet män. Hur många män är det i bassängen?
- Vad skall det stå i rutan för att det linjära ekvationssystemet skall ha oändligt många lösningar?
{2x+5y=35[]x+3y=31
Kommentarer
e-uppgifter (4)
1.
(1/0/0)E C A B P PL M 1 R K 
Ange den ekvation som motsvarar den totala kostnaden för inköp av ett okänt antal toasts och kaffe, då en toast kostar 3535 kr, en kaffe 2020 kr och allt man köpte sammanlagt kostade 145145 kr.
Låt antalet toast motsvara xx och antalet kaffe yy.
Svar:Ditt svar:Rätt svar: 35x+20y=145(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B P PL M 1 R K 
Ange en ekvation som motsvarar sambandet att man sammanlagt köpt 55 varor, där alla varor är antingen en toast eller kaffe.
Låt antalet toast motsvara xx och antalet kaffe yy.
Svar:Ditt svar:Rätt svar: x+y=5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(3/0/0)ME C A B P 1 PL 1 M 1 R K 
En toast kostar 3535 kr, en kaffe 2020 kr och allt man köpte sammanlagt kostade 145145 kr.
Bara toasts och kaffe köptes och totalt 55 varor.Låt antalet toast motsvara xx och antalet kaffe yy.
Hur många toasts och kaffe köptes?
Svar:Ditt svar:Rätt svar: 3 toasts och 2 kaffe(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(4/0/0)E C A B P 1 PL 1 M 2 R K 
Bosse har en massa katter och undulater. Han har totalt 2424 djur och djuren har sammanlagt 8080 ben.
Hur många undulater har Bosse?
Svar:Ditt svar:Rätt svar: 8 undulater(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (11)
5. Premium
(1/3/0)ME C A B P PL 1 M 1 1 R K 1 
Per och Maria köper filmer via nätet. Det är olika pris för nya filmer och för äldre filmer.
Per köper 44 gamla och 22 nya filmer och betalar 600600 kr.
Maria köper 66 nya filmer och 11 gammal och betalar 920920 kr.Vad kostar de gamla respektive de nya filmerna?
Svar:Ditt svar:Rätt svar: Gamla kostar 80 kr och nya 140 kr(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...6. Premium
(0/4/0)E C A B P 1 PL 1 M 1 R K 1 
Vad är priset på en kopp kaffe?
Svar:Ditt svar:Rätt svar: 27 kronor(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(0/1/0)E C A B P PL M R 1 K Vilken graf är den mest korrekta avbildningen av ekvationssystemet?
{f(x)=ax−bg(x)=ax+b
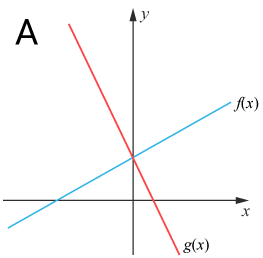
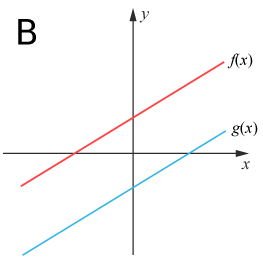
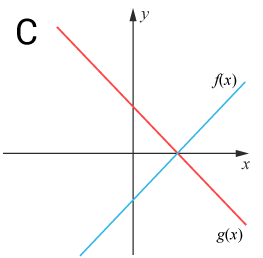
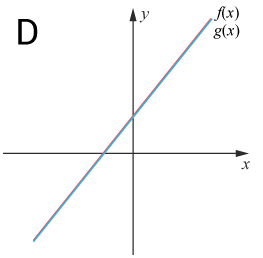 Svar:Ditt svar:Rätt svar: Graf B(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: Graf B(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(0/4/0)E C A B P PL 2 M 1 R K 1 För tre tal gäller följande tre påståenden.
Medelvärdet av det tre talen är 1515.
Differensen mellan största och minsta talet är lika stor som det minsta talet.
Medianen för de tre talen är 55 mer än det minsta talet.Vilka är de tre talen?
Svar:Ditt svar:Rätt svar: 10,15 och 20(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...9. Premium
(0/3/0)E C A B P PL 1 M 1 R K 1 Din vän brukar färga och klippa håret hos frisören. Din vän tycker att det är lite dyrt och överväger att färga sitt hår hemma i stället och vill därför räkna ut hur mycket hon tjänar på att själv göra jobbet.
Färgen kostar 9999 kr om hon gör det själv. Hon minns inte exakt hur mycket det kostar att färga håret, men förra året klippte hon sig sex gånger och färgade det tre och fick totalt betala 42004200 kronor, och om hon färgar och klipper sig på samma gång så brukar det kosta 950950 kr.
Hur mycket sparar hon per gång om hon färgar håret själv?
Svar:Ditt svar:Rätt svar: Hon sparar 401 kronor per gång om du färgar håret själv.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(0/3/0)ME C A B P PL 1 M 1 R K 1 
Elina ska handla godis till sin pappa. Han vill ha 33 hg godis och ger Elina 2020 kr.
I godisaffären finns två olika priser på godis, det billigare kostar 3,903,90 kr/hg och det dyrare kostar 8,908,90 kr/hg.Hur mycket av varje sort kan du handla för att det ska bli precis 2020 kr?
Svar:Ditt svar:Rätt svar: Du kan köpa 1,34 hg av det billiga godiset och 1,66 hg av det dyrare.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...11. Premium
(0/3/0)M NPE C A B P PL M 2 R K 1 Ellen och Irma ska ha en filmkväll och köper läsk och godis. Ellen betalar 8686 kronor för två läsk och fyra godispåsar. Irma köper tre läsk och två godispåsar och betalar 6868 kronor.
Beräkna vad en läsk respektive en godispåse kostar.
Svar:Ditt svar:Rätt svar: En läsk kostar 12,50 kr och en godispåse 15,25 kr.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...12. Premium
(0/3/0)M NPE C A B P PL 2 M R K 1 Bestäm konstanterna aa och bb så att ekvationssystemet {y=ax+1a=y−3x
får lösningen x=3x=3 och y=2by=2b
Svar:Ditt svar:Rätt svar: a=4 och b=6,5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...13. Premium
(0/3/0)ME C A B P PL 1 M 1 R K 1 Darin hade köpt in två sorters kolor för att sälja på en marknad. Lakritskolan köpte hon in för 14,5014,50 kr/hg och hallonkola för 10,5010,50 kr/hg.
Hon gjorde en blandning på totalt 1010 kg av dessa två kolor och sålde blandningen för 2020 kr/hg.
Hon lyckades sälja all kola och när hon dragit av kostnaderna för kolorna hon hade köpt in, hade hon tjänat 870870kr.Hur mycket hade hon köpt av vardera sorten kola?
Svar:Ditt svar:Rätt svar: 20 hg lakritskola och 80 hg hallonkola(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...14. Premium
(0/3/0)E C A B P 1 PL 1 M R K 1 Ange den linjära funktion som uppfyller villkoren
f(4)=−4ƒ (4)=−4 och f(−2)=2ƒ (−2)=2
Ange svaret i kk -form.
Svar:Ditt svar:Rätt svar: y=−x(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...15. Premium
(0/3/0)E C A B P 1 PL 1 M R K 1 Ekvationssystemet
{x+y=ay+ax=1
Har lösningen x=−1x=−1 och y=5y=5
Bestäm talet aa.
Svar:Ditt svar:Rätt svar: a=4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (1)
16. Premium
(0/1/2)ME C A B 1 P 1 PL M R 1 K Ange möjliga värden på aa så att ekvationssystemet {y=2x+1y=−ax–1 har en lösning.
Svar:Ditt svar:Rätt svar: Alla a=−2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Noah Juma
Hej,
#6 är fel skissat,
f(x)=ax−b
g(x)=ax+b
det ska vara: f(x)=ax+b och g(x)=ax-b.
Patrick Cole
Hej!
I uppgift .6 så tjänar du inte en krona, men du sparar säkert endel 😉
David Admin (Moderator)
Sant. Ändrar det i uppgiften.
Krister Ristvedt
Med era svar på a och b skulle omkretsen bli 26cm helt plötsligt? a, långsidan, borde väl bli 7. Och b, kortsidan, borde väl bli 5? Då får man ju omkretsen 24cm. Ser även ut som att i förenklingen av VL, 2a+2(a+2) så multipliceras inte tvåan, och därav blir det fel när man subtraherar med 2 i båda leden därefter som egentligen skulle subtraheras med 4. Eller är jag ute och velar igen?
Måns Normark
Hej,
På övning ett så syns inte bilden som man ska kunna beskriva ekvationssystemet till.
Anna Admin (Moderator)
Det var någon bildlänk som strulade. Hoppas det fungerar nu.
Aksel Nordin
Fråga 1 i övningsdelen, beskriv ekvationssystemet i bilden nedan. Nog för att jag är närsynt, men tycker mig sakna en bild
Tobias Löfgren
Hej
har problem med att räkna ekvationssystemet
2x+7y=8
5x+9y=3
2x+7y=8 delar jag med 2 för att få x fritt
x+3.5y=4
sätter in i ekvation 2
5(4+3.5y) +9y = 3
20 – 17.5y + 9y = 3
17 – 8.5y delat med varandra
y= -2
x+3.5y=4
4-7=-3
x=-3
stämmer detta? känns konstigt med två negativa svar. Ett ska väll vara positivt? Hur blir y positivt när jag delar det med ett negativt tal? säger någon regel att när man delar med ett negativt tal blir det ett positivt tal?
mvh Tobias
Simon Rybrand (Moderator)
Ser ut som att det blir fel när du löser ut x.
2x+7y=8 (-7y)
2x=8−7y
x=4−3,5y
Detta substituerar du sedan in i ekvation 2.
Sandra Palosaari
Hej!
I uppgift 7 står det i lösningen att rätt svar är L = 20 och H = 80. Men det grönmarkerade svaret bland de fyra alternativen är ”10 hg lakritskola och 40 hg hallonkola”.
Tack för en jättebra och pedagogisk sida. Har hjälpt mig jättemycket med matten!
Mvh Sandra
Simon Rybrand (Moderator)
Härligt att höra!
Vi fixar förstås förklaringen!
Michel Tosu
Hej,
svaret på fråga 7 verkar ha blivit fel. Förklaringen till svaret motsäger själva svaret. Jag vill inte skriva svaret här men jag tolkar det som att svaret diskuterar att två alternativ är möjliga här men sedan säger ni varför endast ett alternativ är korrekt men svaret är det andra alternativet.
Om jag inte misstar mig? 🙂
Simon Rybrand (Moderator)
Hej
Nej du misstar dig inte, vi fixar det!
Pierre Nilsson
En fråga. I matteboken så visar de att i additionsmetoden ska man multiplicera alla talen.
Ta t.ex det talet ni visar i början på videon med x+2y=0 där ska alla talen multipliceras med -2. Men nollan är oförändrad i videon. Jag trodde det skulle se ut så här -2x – 4y=-2 ?
Simon Rybrand (Moderator)
Hej!
Om du multiplicerar 0 med ett tal så kommer du få svaret 0. Exempelvis:
3⋅0=0
2543⋅0=0
0⋅(−4)=0
Noll multiplicerat med ett tal är alltid noll.
at1981
Hejsan!
Ni får facit av mig! Men ni som är mattegenier får gärna visa hur man kommer fram till detta resultat!
X = 150
Y = -200
Z = 3
Jag meddelar att det är Excel och dess smarta funktioner som skött uträkningen!
Med vänliga hälsningar at1981 !!
Simon Rybrand (Moderator)
Hej
Det går att lösa ekvationssystem med både additionsmetoden och substitutionsmetoden även om substitutionsmetoden mest används för enklare ekvationssystem med två ekvationer och två okända variabler. Sedan används heller additionsmetoden och en metod som kallas för gausselimination.
hano
hej kan du hjälpa mig att lösa 2 lg x .0,5 lg x ^2 tack
Simon Rybrand (Moderator)
Hej
Vad skall du göra med uttrycket? Skall du förenkla det eller är det något annat som du skall göra?
Det står en punkt . i ditt uttryck, innebär det en multiplikation?
Marko
Hej! Har fastnar helt…. Ett rederi ger 30% rabatt till studerande. Vid en överfart var 245 personer ombord på färjan, varav 55 var studerande. Rederiet fick in 47 985 kr i biljettavgifter. Hur mycket betalar en studerande för överfarten? Lös uppgiften med hjälp av en ekvation.
Simon Rybrand (Moderator)
Hej, om normalpriset är x så betalar alltså en student 0,7x kronor (förändringsfaktorn är 0,7).
Det är 245-55=190 stycken som inte är studenter.
Vi kan då ställa upp ekvationen
55⋅0,7x+190⋅x=47985⇔
38,5x+190x=47985⇔
228,5x=47985⇔
x=228,547985=210
En student betalar alltså 0,7⋅210=147 kr
Ditte Jardmark
Hej! jag försöker lösa ut följande tal men när jag byter metod får jag ett annat resultat. Jag hittar inte var jag gör fel:( trodde verkligen att jag hade koll på detta nu!
y=x+2
y=-1x+1
så här har jag räknat:
x+2=-1x+1
x+2+1x-2=-1x+1+1x-2
2x=-1
x=-0,5
y=1,5
additionsmetoden
x+2=y
-1x+1=y
x+(-1x)+2+1=2y
3=2y
2/3=y
Y är 0.67 avrundat
Jag hittar inte felet
Simon Rybrand (Moderator)
Felet ligger när du löser det med additionsmetoden på slutet, dvs
3=2y
där du skall få att
y = 3/2 = 1,5 och inte 2/3.
Simon Rybrand (Moderator)
Kalla fasta kostnaden för a och rörliga för b:
a+6b=3800
Sedan kallar du den nya fasta kostnaden för (0,9a) och nya rörliga för (1,2b) vilket ger ekvationen
(0,9a)+5(1,2b)=3750
Dessa två ekvationer kan du använda och ställa upp ett ekvationssystem!
maggie liew
Toppen,nu fick jag fram svaret!!, tack för hjälpen, Simon.
maggie liew
Hej jag kommer bli jätte tacksamt om jag får hjälp att löser denna frågan, i hade gjort många försökt men fick jag inte fram rätt svar.
En faktura består av en fas kostnad och en timkostnad. Vid ett tillfälle blev kostnaden 3800 kr för 6 timmar arbete. Därefter sänkte den fasta kostnaden med 10% samtidigt som timavgiften höjdes med 20%, och man fick då betala 3750 kr för 5 timmar arbete. Bestäm den fasta kostnaden och timkostnaden FÖRE förändringen.
Caroline
05:58 i videon, den röda linjen. När jag går ett steg till vänster och sedan räknar hur många steg det är upp så får jag ju inte 2x. Det är ju snarare 1x (x alltså).
Samma sak vad gäller den blå linjen som är negativ och ska vara -X, den är ju lite mer än -X? Om jag räknar på samma sätt där liksom.
Gör jag fel eller har ni inte markerat exakt i videon?
Simon Rybrand (Moderator)
Hej,
Vi har inte markerat exakt i videon utan har gjort en ”skiss” av hur det ser ut. man skulle förstås relativt enkelt kunna göra en mer exakt beskrivning (även om en bild alltid blir mer eller mindre ungefärlig) men det är också bra att kunna lösa uppgiften utifrån linjernas ekvationer med k och m värdena.
Fredric Hallgren
Hej! Jag har räknat mig galen på ett tal jag har i matematik 2. Jag kan inte hitta rätt video för att få svar på talet.
Vilket värde skall a ha för att en rät linje med riktningskoefficienten 2 skall gå genom punkterna (a − 1, 2) och (−2, a + 2) ?
Oerhört tacksam för svar.
PS. Den här sidan kommer bli min räddning när det kommer till Ma 2. Jag har er att tacka för mina studier dom kommande åren!
Simon Rybrand (Moderator)
Hej!
Vi har ingen video med just exakt en sådan uppgift.
Du kan där använda dig av formeln för k och beräkna/förenkla
k=−2−(a−1)(a+2)−2=−1−aa
Eftersom att du vet att k = 2 så kan du nu ställa upp ekvationen
−1−aa=2⇔ Multiplicera med (-1-a)
a=2(−1−a)⇔
a=−2−2a⇔
3a=−2⇔
a=−32
Elias
Hej sitter fast på en fråga, hur löser man på det här, ( värde på a )
Ax+2y=6
9x+3y=12
Simon Rybrand (Moderator)
Hej
Får du någon mer information kring uppgiften? Det är tre okända och två ekvationer vilket gör att det finns flera lösningar.
Mikael144600
Hej!
Tack för ett snabbt svar. Nja, jag förstår att a måste ha ett negativt värde eftersom minus gånger minus blir plus och att linjen måste ha en positiv lutning. Om a varit lika med -2 så hade linjerna blivit parallella.
Men, om a inte är lika med 2, skulle a kunna vara lika med 0 eller större än 2. I dessa fall kommer väl inte linjerna heller att korsas i 1:a kvadranten?
Simon Rybrand (Moderator)
Hej
Jag plockade bort formuleringen kring att de måste korsa varandra i den första kvadranten, förstår att detta är lätt att missa men jag tror att uppgiften blir lättare att tolka och förstå då.
Mikael144600
Hej!
Jag tror jag har snurrat till det för mig på uppgift 3.
När jag ritar ut den andra ekvationens linje så är den ena punkten på linje vid (0,-1) eftersom m=-1.
För att linjen ska skära den första ekvationens linje så får inte a vara lika med 0 eftersom då skär inte linjerna varandra i 1:a kvadranten.
A får inte heller vara 2 eftersom då blir linjerna parallella. Alltså måste a vara större än 0 men mindre än 2. I facit står det att a ska vara större än 2 (a > 2).
Vad är det jag har missat?
Simon Rybrand (Moderator)
Hej
Du har inte missat något utan uppgiften var otydligt formulerad och svaret likaså.
Vi har uppdaterat uppgiften så att den är lite annorlunda formulerad samt lagt till en korrekt förklaring kring denna.
Hoppas att detta gör det tydligare hur man kan resonera kring uppgiften.
competens
hej i uppgift 2 ) forstar jag inte hur det blev -4x – 24y = 3680
sen ar det -22y = -3080
y = 140
x = 80
kan du hjalper mig for jag forstar inte hur det blev sa
Simon Rybrand (Moderator)
Hej, där används den metod som kallas för additionsmetoden vilken innebär att de två ekvationerna adderas med varandra.
Vi har innan additions utförts multiplicerat varje term i den andra ekvationen med -4. Detta görs för att vi skall få 4x i den ena ekvationen och -4x i den andra. När dessa sedan adderas med varandra så kommer x -termerna att eliminera (ta ut) varandra och vi kan lösa ut y.
Kika gärna på videon om additionsmetoden. Då tror jag att du kommer att förstå resonemanget bättre bakom detta.
jelica
För vilket värde på a saknar ekvationssystemet nedan lösning:
ax+2y=6
ax+3y=12
Simon Rybrand (Moderator)
Hej, ett linjärt ekvationssystem saknar lösning när de två linjerna som varje ekvation representerar är parallella. Dvs då de aldrig skär varandra. Du kan därför skriva om ekvationssystemet till
y = -a/2x + 3
y = -a/3x + 4
så att du ser respektive k-värde tydligare. Här kan vi se att om a = 0 så kommer de att ha samma lutning.
Mikael Forsberg
I uppgift 3 så ger ni svaret att a>2. Jag undrar hur detta stämmer för a=3 då uppgiften ger att vi söker skärningen mellan linjerna y=2x+1 och y=-3x-1. I detta fall så blir
lösningen x=-2/5 och y=1/5, dvs ett negativt x-värde!
Jag tror att svaret borde vara a<-2 eller att uppgiften ska ha y=+ax-1 som andra ekvation
Gratulerar annars till en fin undervisningssajt!
Med vänlig hälsning, 🙂
mikael forsberg
universitetslektor i matematik vid Högskolan i Gävle
Simon Rybrand (Moderator)
Hej Mikael och tack för din kommentar.
Jag har korrigerat frågeställning och förklaring så att det skall vara korrekt.
samuel N.jr
hur löser man ekvationen om den ser ut på det här sättet:
y-2x+3=0
2x+y-53=0
y-x-11=0
Simon Rybrand (Moderator)
Hej, egentligen på ungefär samma vis. Du kan tex lösa ekvationssystemet
y-2x+3=0
2x+y-53=0
som har lösningen x = 14 och y = 25.
Nu kan vi kolla att punkten (14, 25) ligger på linjen y-x-11=0 genom att sätta in dessa värden:
25-14-11 = 25-25 = 0.
Så den lösningen är alltså korrekt.
Enegine Höfer
Hej.
Jag har en stor hopp när se er sidan.
Tacksam om jag kommer få en hjälp för en
) För vilket värde på a saknar ekvationssystemet nedan lösning?
ax + 2y =6
9x + 3y =12?
Simon Rybrand (Moderator)
Skriv om ekvationerna på räta linjens ekvation. dvs att
y = -ax/2 + 3
y = -3x + 4
Ekvationssystemet saknar sedan lösning när linjerna har samma k – värde, dvs då
−a/2=−3
sarwa
har du dividera 6 med 2 eller hur har du hittat 3 ?
Simon Rybrand (Moderator)
Ja precis, vi vill få y ensamt och eftersom vi där har 2y så divideras alla termer med 2.
Nathalie
Hejsan, jag förstår inte riktigt, behöver hjälp med denna uppgift och vore tacksam för svar, hur ska jag ställa upp ekvationen?
Om man köper 2 kg apelsiner och 3 kg vindruvor får man betala 183 kr. Om man i stället köper 1,5 kg apelsiner och 1 kg vindruvor kostar det 76 kr. Vad kostar 1 kg vindruvor?
Simon Rybrand (Moderator)
Hej, sätt
x = kilopris apelsiner
y = kilopris vindruvor
Du kan då ställa upp ekvationssystemet
2x + 3y = 183
1,5x + y = 76
MAXI
I uppgift 3, hur ska man veta att det är meningen linjerna ska skära varandra då?
Det står ingenstans i uppgiften, utan det villkoret ges ju först
sen i lösningen?
Simon Rybrand (Moderator)
Hej, tanken är i den uppgiften att man behöver känna till att en lösning till ett ekvationssystem med två linjära ekvationer alltid ges där linjerna skär varandra.
MAXI
Okej, men hur ser det ut när man har två linjer som inte skär varandra?
Skriver man det på nåt särskilt sätt?
Simon Rybrand (Moderator)
Om två linjer inte skär varandra så kommer de linjerna att vara parallella. Då kan man nämna att det inte finns någon lösning till ekvationssystemet och att de linjer som representeras av ekvationssystemet är parallella.
Clara
Hej! Skulle jag kunna få hjälp med dessa? 🙂
1. Lös ekvationssystemet
x+y=21
x-y=-9 med valfri algebraisk metod.
2. Lös ekvationssystemet
y=0,5x+2,5
y=3x-1 med valfri algebraisk metod
Simon Rybrand (Moderator)
Hejsan, jag kan visa dig den första så kan du säkert klara av den andra själv.
x+y=21 (1)
x-y=-9 (2)
————
Här skulle vi exempelvis kunna börja med ekvation (1) och omforma den så att x står ensamt på ena sidan om likhetstecknet, då får vi:
x+y=21⇔
x=21−y
————-
Nu kan vi substituera (substitutionsmetoden) x i den ekvation (2) mot (21-y) och får då
(21−y)−y=−9⇔ (förenkla VL)
21–2y=−9⇔ (-21)
–2y=−30⇔ (/-2)
y=15
————
Nu känner vi till y = 15 och sätter in det i ekvation (1) så att vi kan ta reda på x-värdet:
x=21−15=6
————-
SVAR:
x = 6
y = 15
Clara
2. Lös ekvationssystemet
y=0,5x+2,5
y=3x-1 med valfri algebraisk metod
är inte säker ifall jag får rätt svar på denna, kan du hjälpa mig med den?
Simon Rybrand (Moderator)
Där har du y i bägge ekvationerna ensamt så du kan sätta
0,5x+2,5 = 3x-1 (+1)
0,5x+3,5 = 3x (-0,5x)
3,5 = 2,5x
x = 3,5/2,5 = 1,4
och y blir 3*1,4 -1 = 3,2
caitlin
Hej, kul att hittar er på denna hemsidan. Skitbra!
Kan du hjälpa mig att förstår hur man räknar ut :
Lös ekvationssytemen på algebraisk ?
Y=5-0,5x
4x+6y-25=0
Hur ska jag tänka?
Simon Rybrand (Moderator)
Hej,
Först behöver du bestämma dig om du vill använda substitutionsmetoden eller additionsmetoden. I det här fallet så är det nog smidigast med substitutionsmetoden då du har y ensamt i den första ekvationen.
(1) y=5-0,5x
(2) 4x+6y-25=0
Substituera y i (2) mot (1):
4x+6(5−0,5x)−25=0
4x+30−3x−25=0
x+5=0
x=−5
Sätt nu in detta i (1)
y=5+2,5=7,5
Endast Premium-användare kan kommentera.