
Att härleda exakta trigonometriska värden
2016-03-29 Av Simon Rybrand 4 kommentarer
Du som läser en kurs på gymnasiet som innehåller trigonometri har säkerligen ett flertal gånger suttit och kikat i formelbladet för att ta reda på exakta trigonometriska värden. De allra flesta av oss är förstås nöjda med att denna information finns i formelbladet men det kan också vara intressant att ta reda på hru man faktiskt kan härleda exakta trigonometriska värden.
I det här blogginlägget tänkte jag visa några av dessa härledningar för dig som är intresserad av detta. Det är faktiskt inte särskilt svårt så blir inte avskräckt utan ge det en chans. Dessutom är det mycket bra träning på att förstå geometri, trigonometri och enhetscirkeln.
Exakta värden för vinkeln $45°$
När vi skall ta fram värden för sinus, cosinus och tangens så kan vi utgå från en kvadrat med sidorna 1. Vi drar en diagonal mellan två av hörnen och denna blir då enligt pythagoras sats $\sqrt{2}$ och vinkeln nere vid diagonalen blir $45°$. En bild på detta ser ut på följande vis:
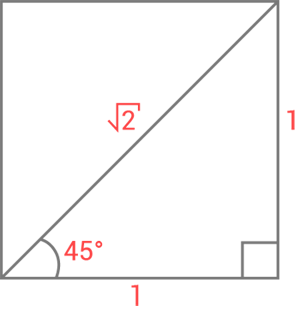
Vi kan nu få fram exakta trigonometriska värden för sinus, cosinus och tangens. Dessa är
$ tan(45°)=\frac{\text{motstående katet}}{\text{närliggande katet}} = \frac11=1 $
$ sin(45°)=\frac{\text{motstående katet}}{\text{Hypotenusan}} = \frac{1}{\sqrt{2}}= $ $\frac{1·\sqrt{2}}{\sqrt{2}·\sqrt{2}}=\frac{\sqrt{2}}{2} $
Vi förlänger täljare och nämnare med $ \sqrt{2} $ så att vi får heltalsnämnare.
$ cos(45°)=\frac{\text{motstående katet}}{\text{Hypotenusan}} = \frac{1}{\sqrt{2}}= $ $\frac{1·\sqrt{2}}{\sqrt{2}·\sqrt{2}}=\frac{\sqrt{2}}{2} $
Vi förlänger täljare och nämnare med $ \sqrt{2} $ så att vi får heltalsnämnare.
Exakta värden för vinkeln $60°$ och $30°$
För att få fram exakta trigonometriska värden för $60°$ och $30°$ så använder vi istället en liksidig triangel, dvs en triangel där alla sidor är lika långa och alla vinklar är $60°$. Sidorna i den liksidiga triangeln är alla 1. Vi markerar även ut höjden och vinkeln $30°$ uppe vid toppen på triangeln och att halva längden på bassidan är $0,5$.
Vi kan också beräkna höjden med pythagoras sats så vi får den till $ \sqrt{1^2-(\frac12)^2}=\sqrt{1-\frac14}=\sqrt{\frac34}=\frac{\sqrt{3}}{2} $.
Med en bild ser detta ut på följande vis:
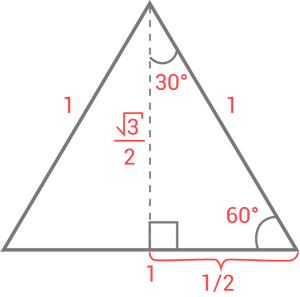
Nu använder vi figuren för att ta fram de exakta trigonometriska värdena.
$tan(30°)=\frac12 \big/ \frac{\sqrt{3}}{2} = \frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}$
$sin(30°)=\frac12 \big/ 1 = \frac{1}{2}$
$cos(30°)=\frac{\sqrt{3}}{2}\big/ 1 = \frac{\sqrt{3}}{2}$
Exakta värden för vinkeln $60°$ blir
$tan(60°)= \frac{\sqrt{3}}{2} \big/ \frac12 = \frac{2\sqrt{3}}{2}=\sqrt{3}$
$sin(60°)=\frac{\sqrt{3}}{2}\big/ 1 = \frac{\sqrt{3}}{2}$
$cos(60°)=\frac{1}{2}\big/ 1 =\frac12$
Exakta värden för vinklarna $0°$, $90°$, $180°$, $270°$ och $360°$
När det gäller vinklarna $0°$, $90°$, $180°$, $270°$ och $360°$ så kan vi utgå från enhetscirkeln för att ta fram dessa värden. På enhetscirkeln gäller att radien är $1$ och att
$sin v = \frac{y}{1} = y$ (y-koordinaten på cirkelns rand)
$cos v = \frac{x}{1} = x$ (x-koordinaten på cirkelns rand)
Tangens för de olika värdena får genom sambandet $ tanv=\frac{sinv}{cosv} $
Med en bild ser detta ut på följande vis.
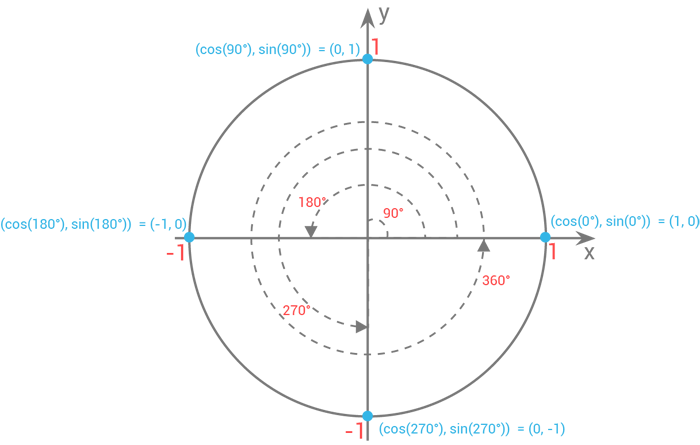
Alla värden här är alltså
| Vinkel | $sinv$ | $cosv$ | $tanv=\frac{sinv}{cosv}$ |
| 0° | 0 | 1 | 0/1 = 0 |
| 90° | 1 | 0 | 1/0 ej definierat! |
| 180° | 0 | -1 | 0/-1 = 0 |
| 270° | -1 | 0 | -1/0 ej definierat! |
| 360° | 0 | 1 | 0/1 = 0 |
Exakta värden för vinklarna $120°$, $135°$ och $150°$
Vi kan även använda oss av att vi vet exakta värden för vinklarna $30°$, $45°$ och $60°$ samt det vi vet om enhetscirkeln för att ta fram exakta trigonometriska värden för $120°$, $135°$ och $150°$. Det vi då använder oss av är att $ 180°-60°=120° $, $ 180°-45°=135° $ och $ 180°-30°=150° $. Vi kan rita ut dessa vinklar på följande vis:
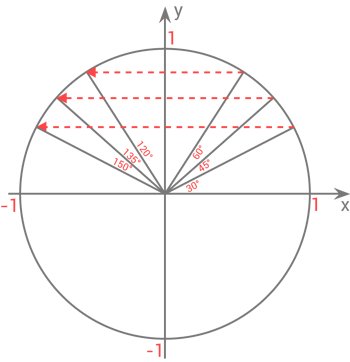
Det som är viktigt att uppmärksamma i den här bilden är att vinkeln $60°$ är på samma höjd som vinkeln $120°$, dvs den har samma y-värde men x-värdet har bytt tecken till minus. På samma vis är det med vinklarna $45°$ och $135°$ samt vinklarna $30°$ och $150°$.
Alltså kan vi sammanställa de exakta trigonometriska värdena i följande tabell.
| Vinkel | $sinv$ | $cosv$ | $tanv=\frac{sinv}{cosv}$ |
| 120° | $\frac{\sqrt{3}}{2}$ | $-\frac12$ | $-\sqrt{3}$ |
| 135° | $\frac{\sqrt{2}}{2} $ | $-\frac{\sqrt{2}}{2}$ | $-1$ |
| 150° | $\frac{1}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{\sqrt{3}}{3}$ |
Härleda exakta trigonometriska värden – Sammanfattning i tabell
Nu är vi redo att samla alla dessa exakta trigonometriska värden i en tabell som liknar det du hittar i formelbladet.
| Vinkel | $sinv$ | $cosv$ | $tanv=\frac{sinv}{cosv}$ |
| 0° | 0 | 1 | 0 |
| 30° | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{3}}$ |
| 45° | $\frac{\sqrt{2}}{2} $ | $\frac{\sqrt{2}}{2} $ | 1 |
| 60° | $\frac{\sqrt{3}}{2}$ | $\frac12$ | $\sqrt{3}$ |
| 90° | 1 | 0 | ej def. |
| 120° | $\frac{\sqrt{3}}{2}$ | $-\frac12$ | $-\sqrt{3}$ |
| 135° | $\frac{\sqrt{2}}{2} $ | $-\frac{\sqrt{2}}{2}$ | $-1$ |
| 150° | $\frac{1}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{\sqrt{3}}{3}$ |
| 180° | 0 | -1 | 0 |
| 270° | -1 | 0 | ej def. |
| 360° | 0 | 1 | 0 |
Hej!
Jag undrar om jag vet att cos v = 3/5
Hur tar jag reda på sin v?
Ta reda på vilken vinkel v det är först med arccos. Sedan beräknar du sinusvärdet för den vinkeln.
För vinklar under rät vinkel (90°): rita en rätvinklig triangel med hypotenusan 5 längdenheter (le) och med kateten 4 le närmast din vinkel. Pythagoras sats ger den andra kateten till 3 le. Sinusvärdet är kvoten mellan den motstående kateten och hypotenusan, dvs 3/5 = 0,6.
För att finna alla vinklar med sinusvärdet 0,6 så rita in din triangel i en enhetscirkel.
För att undvika att framtida läsare blir konfunderade: Gunnar svarade av misstag på frågan om hur man tar reda på sin v om man vet att cos v = 4/5. Inte 3/5, som Sofia frågade om.