-registrering
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Högskoleprovet matematik
/ KVA provpass 2 – Uppgift 18 till 22
KVA provpass 2 - Uppgift 18 till 22
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Innehåll
Exempel i videon
- x > 0 och Kvantitet I: x⁻²/2, Kvantitet II: (x/2)⁻².
- L₁ och L₂ är parallella linjer och punkterna A,B,C och D ligger på dessa linjer. AD är längre än AC. Kvantitet I:arean av triangeln
ABC, Kvantitet II: arean av triangeln ABD. - k, m och n är heltal och 0 < k < m < n. Kvantitet I: m/n, Kvantitet II: k/m.
- Kvantitet I: x^(1/4), Kvantitet II: √(√(x)).
- x och y är positiva heltal och att 5x + 10y = 270 580. Kvantitet I: x, Kvantitet II: y.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (5)
-
1. Premium
y < z och x < m < y och z < n < w
Kvantitet I: m
Kvantitet II: nBedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
2. Premium
Kvantitet I: $ \frac{355}{113} $
Kvantitet II: 3,1
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
3. Premium
ABCD är en rektangel
Kvantitet I: Omkretsen av rektangeln ABCD
Kvantitet II: 18 cm
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
4. Premium
x + 5 > 2 och y – 3 < 7
Kvantitet I: x
Kvantitet II: y
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
5. Premium
A jobbar x timmar per dag och tjänar y kronor per timme. B jobbar 20 % längre tid per dag än A och tjänar 90 % av vad A tjänar per timme.
Kvantitet I: A:s förtjänst under 10 arbetsdagar
Kvantitet II: B:s förtjänst under 10 arbetsdagar
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar...
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Gustav Engström
Hej!
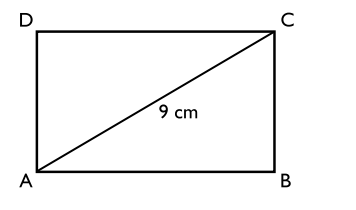
Jag undrar kring övning nr 3. När jag räknar får jag det till att kvantitet I & II är lika stora. Tänker att AB^2 + BC^2 = 9^2
AB + BC bör därför vara = 9.
Hur ska man tänka för att komma fram till: 8<AB+BC+CD+AD=omkretsen?
Mvh
Simon Rybrand (Moderator)
Med hjälp av AB^2 + BC^2 = 9^2 vet du inte att AB+BC=9.
Du kan bara säga att AB+BC>9 pga att diagonalen måste vara mindre än de två sidorna tillsammans.
Sedan kan hela omkretsen skrivas som 2*(AB+BC)
anatomi
På uppgift 5 i testet kan det vara enklare/snabbare att bara multiplicera 113 med 3,1 och jämföra med I:s täljare.
anatomi
Uppgift 3 menar jag! (Vet inte hur man redigerar inlägg).
Simon Rybrand (Moderator)
Tack för en alternativ lösning!
Yosef123
På proven brukar det förekomma såna tal som i uppgift 20 men oftast går det att sätta siffror till variablerna , hur rekommenderar du att man ska tänka och hur man kan veta om det går eller om det inte går?
drkaratechop
I uppgift 20, förstår jag inte varför man inte får ge siffror till alla variablerna. Om man följer regeln om att 0 < k < m < n, så kommer alltid (?) kvantitet 1 vara större än 2. om man väljer k=1, m=2, n=3.. eller k=4, m=17, n=60 :/
Simon Rybrand (Moderator)
Om vi väljer
n = 10
m = 2
k = 1
Så är
$ \frac{m}{n} = \frac{2}{10} = 0,2 $
$ \frac{k}{m} = \frac{1}{2} = 0,5 $
vilket motsäger ditt resonemang. Det går också att välja andra n, m, k så att istället kvantitet II är större.
Isak Hassbring
Hej,
Tänkte bara notera att det i Uppg 18 räcker med att förenkla Kvantitet II ett steg (dvs ”ta bort” paranteserna).
Båda täljarna är då X^-2 och nämnarna är lätta att jämföra (ena är 2 och andra är 2^-2).
Då ser man direkt att Kvantitet I är större än Kvantitet II.
Kanske kan hjälpa någon att spara tid. Tack för mig!
Minaslan
Hejsan!
Tack för denna sida! Dina videos har hjälpt mig massor! Hur gjorde du på uppgift 18 Kvantitet II ? Varför byter du plats på täljare resp. nämnare?
Simon Rybrand (Moderator)
Hej,
Anledningen till att jag byter plats är för att det då blir enklare att jämföra de två kvantiteterna med varandra. De liknar varandra mer då och det är lättare att se vilken som är störst.
Regeln som används för att göra det är följande potensregel:
$ a^{-b} = \frac{1}{a^b} $
Vi kan också skriva denna regel som
$ \frac{a^b}{c^d} = \frac{c^{-d}}{a^{-b}} $
Hoppas att detta hjälper dig vidare. Om du har egna lösningmetoder eller idéer så går det bra att skriva dem. Det kommer då fler som pluggar HP till del.
Endast Premium-användare kan kommentera.