-registrering
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Högskoleprovet matematik
/ Högskoleprovet VT 2013 – Svårare uppgifter
KVA provpass 4 - Uppgift 18 till 22
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Innehåll
Exempel i videon
- f(x) = 3x + 1, Kvantitet I: f(a) – f(a+1), Kvantitet II: 3.
- Kvantitet I: Medelvärdet av (3x+4y+z+38) och (x+y+z+94), Kvantitet II: Medelvärdet av (4x+2z+94) och (5y+51).
- För triangeln ABC gäller att vinklarna är x > y > z. Kvantitet I: x + y, Kvantitet II: 120°.
- a > 0, b > 0 och c < 0 samt att a = b + c. Kvantitet I: a, Kvantitet II: b.
- n≥0, m≥0 och n och m är heltal. Kvantitet I: $(n+1)^m$, Kvantitet II: $m^{(n+1)}$.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (5)
-
1. Premium
$7^2 + x – 2 = 1$
Kvantitet I: $x^2 + x – 2 $
Kvantitet II: $0 $
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
2. Premium
Linjerna $L_1$ och $L_2$ ges av nedanstående ekvationer, där y är en funktion av x.
$L_1$: $ -\frac16y+\frac13x=\frac12 $
$L_2$:$ -y+3x=-18 $
Kvantitet I: Lutningen för linjen $L_1$
Kvantitet II: Lutningen för linjen $L_2$
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
3. Premium
Rektanglarna $R_1$ och $R_2$ har lika stor area.
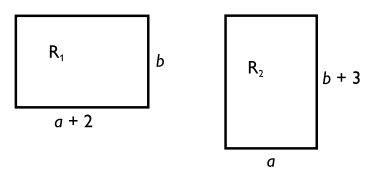
Kvantitet I: a
Kvantitet II: b
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
4. Premium
Kvantitet I: $ \sqrt{10- \left(\frac{0,4}{\sqrt{0,16}} \right) } $
Kvantitet II: 3
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
5. Premium
$ 4≤ x ≤ 10 $
$ 1≤ y ≤ 6$
$3≤ z ≤ 8$Kvantitet I: Medelvärdet av x, –y och –z
Kvantitet II: Medelvärdet av –x, y och z
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar...
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
Din skolas prenumeration har gått ut!
David Magnusson
Tack för jättebra filmer! Fråga 19 handlar däremot inte om att faktiskt lösa uppgiften, utan om att direkt se att man kan stryka termer i frågan.
Eftersom man söker medelvärdet ska båda kvantiteterna delas med 2, alltså behöver ingen av kvantiteterna delas med 2 för att de ska kunna jämföras.
Jämför vi sen snabbt alternativen ser man att de båda innehåller termerna 4x+5y+2z+94 vilket direkt kan strykas.
Den egentliga frågan är alltså vilket som är störst av 38 eller 51.
Variablerna, parenteserna och divisionen är bara där för att förvirra och göra att man lägger mer tid än nödvändigt frågan. Bland det svåraste i provet är ju just att avgöra vad man snabbt kan lösa utan långa beräkningar, och provmakarna verkar älska att förvirra just med den typen av frågor!
David Admin (Moderator)
Tack David, för din input!
Självklart kan man göra som du säger. Och ju mer man tränar på dessa exempel, ju lättar får man för att se det system du beskriver! Målet är, som du säger, att slippa räkna och bara ”se” svaret.
Sara
I fråga 19, skulle inte x, y eller z eller alla tre kunna vara negativa och man därför inte säkert kan veta vilken av kvantiteterna som är störst?
Simon Rybrand (Moderator)
Hej
Eftersom att de är lika så spelar det ingen roll om de är negativa eller positiva, de kommer ändå att vara lika stora. Skillnaden ligger i täljarnas 132 och 145 där 145 är större.
Crixus
Fråga 18) f(a) = 3a + 1
Varför blev det 3a?
Tack
Simon Rybrand (Moderator)
Hej, vi har ju där $ f(x) = 3x+1 $ och när vi beräknar $f(a)$ så byter vi ut $x$ mot $a$ så att vi får $ 3x+1 $. Hjälper detta? Ett tips kan också vara att kika på genomgången om vad en funktion är, det kan nog hjälpa till att bättre se varför du får detta här.
hussein radhi
i uppgift 19 hur kunde du dela med två? summan av siffrorna delat med antalet siffror. men bad är antalet siffror?
Simon Rybrand (Moderator)
Hej, här får du se hela det algebraiska uttrycket som ”ett tal”. Dvs om man skulle sätta in värden istället x, y och z så skulle du få ett tal. Därmed har du två tal och för att få medelvärdet delas med 2.
Endast Premium-användare kan kommentera.