Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 4
/ Komplexa tal och Polynom
Problemlösning Komplexa tal
Innehåll
Komplexa tal
De komplexa talen ger oss möjlighet att lösa ekvationer där vi har ett negativt tal under rottecknet.
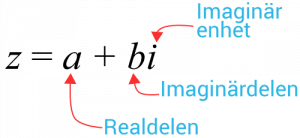
Komplexa tal består av en reell och en imaginär del. Genom att införa den imaginära enheten $i$i, som definieras som ett tal med egenskapen $i^2=-1$i2=−1, kan vi skriva om negativa tal till imaginära tal och lösa tidigare olösbara ekvationer.
Exempelvis är $\sqrt{-9}=\sqrt{9i^2}=3i$√−9=√9i2=3i
Formler och begrepp som används i videon och övningar Premium
Komplext tal
Allmänt brukar man beskriva ett komplext tal som $ z = a + bi $
där a är realdelen och b imaginärdelen.
Absolutbeloppet
Om $ z = a+bi $ gäller att
$ |z|=|a+bi|=\sqrt{a^2+b^2} $
Komplexa konjugatet
Om $ z = a+bi $ gäller att
$ \overline{z}=a-bi $
Argumentet
Om $ z = a+bi $ gäller att
$Arg(z) = v = arctan(\frac{b}{a}) $.
Multiplikation av komplexa tal på polär form
Om $ z=r_1(cosv_1+isinv_1) $ och $ q=r_2(cosv_2+isinv_2) $ gäller att
$ z⋅q = r_1⋅r_2(cos(v_1+v_2)+isin(v_1+v_2)$
Division av komplexa tal på polär form
Om $ z=r_1(cosv_1+isinv_1) $ och $ q=r_2(cosv_2+isinv_2) $ gäller att
$ \frac{z}{q} = \frac{r_1}{r_2}(cos(v_1-v_2)+isin(v_1-v_2)$
De Moivres Formel
$(r(cos(v)+isin(v))^n=r^n(cos(n \cdot v)+isin(n \cdot v))$
Exempel i videon Premium
- Låt $z=2+2i$
a) Ange $ \overline{z} $
b) Bestäm $|z|$
c) Skriv $z$ på polär form. - Skriv det komplexa talet $ \frac{4i}{1+i}+i $ på formen $a+bi $.
- Lös ekvationerna
a) $x^2+38x+557=0$
b) $z^2=i$ - Beskriv det område i det komplexa talplanet som beskrivs av $ |z|<4 $ och där $z$ är ett komplext tal.
- Lös fullständigt ekvationen $ w^3=-8 $ och svara på formen $a+bi $.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (3)
-
1. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B 1 P PL M R K Vilket olikhet beskriver det markerade området i det komplexa talplanet?
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P 1 PL M R K Bestäm $|z|$|z| då $z=8+15i$z=8+15i .
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar...3. Premium
Rapportera fel Ändra till korrekt (2/0/0)M NPE C A B P 2 PL M R K Lös ekvationen $z^3=-27i$z3=−27i
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar...Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut! -
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
John Winlund
Det står ju bara z^3 = -i på 3e uppgiften, hat ni glömt att skriva dit 27?
Simon Rybrand (Moderator)
Hej
Den siffran verkar ha fallit bort där, vi har korrigerat detta, tack för att du sade till!
Simon Rybrand (Moderator)
Här gäller att du får kika på de tabeller med exakta trigonometriska värden som finns där man kan hitta att vinkeln $ \frac{5 \pi}{3} $ har
$ sin(\frac{5 \pi}{3}) = – \frac{\sqrt{3}}{2} $
linnrehn
Kan du förklara hur du skriver om (+isin5pi/3) till (-i”roten ur”3/2)
P.S. Tack för sjukt hjälpsamma videor!!
John Winlund
Test fråga nr 3, ska det inte stå z^3 = -27i ? Eller har jag missat något?
Anne
Varför blir det minus i på sista lösningen och hur får du 5 pi/3 till 1/2?
Simon Rybrand (Moderator)
Hej,
Det kan vara bra att ha framme ett formelblad på dessa uppgifter då man här använder att vissa trigonometriska värdens exakta värde finns samlade där. Kika där och se vilket värde 5pi/3 har. Detta svarar även på din fråga om varför det blir minus.
kajsanordqvist@hotmail.se
Hej! Jag kollade i mitt formelblad och ser att 5pi/6 är lika med 1/2.
Det står däremot inget om att 5pi/3 är lika med 1/2. 5pi/3 finns inte med. Ska man förenkla på något sätt?
Tack på förhand
Simon Rybrand (Moderator)
Hej
Det brukar vara så att lite olika exakta trigonometriska värden finns med i formelbladen. Vissa formerblad har endast några få med medan andra har väldigt många olika värden med. Om man kräver kunskap om några exakta trigonometriska världen på ett prov så bör ju dessa finnas med i formelbladet. Jag skulle i så fall kunna vara så att det man söker kunskap om att kunna ta fram ett exakt trigonometrisk värde, då är det ju framförallt enhetscirkeln som man använder sig av.
Hoppas att detta svara på din fråga, säg till annars så fortsätter vi diskussionen om detta.
evgeniydonev
Jag fastnade på samma uppgift som Melker lite längre upp. Tur att jag såg på kommentarerna. Fans risk att jag började tvivla på min förmåga att lösa, annars inte så svåra uppgifter, som denna.
Föreläsningarna är annars riktig bra.
Tack Evgeniy
Simon Rybrand (Moderator)
Hej Evgeniy och tack för att du kommenterade detta. Jag uppdaterade videon redan vid förra kommentaren (trodde jag) men tydligen verkar det inte ha fungerat. Jag har nu återigen uppdaterat videon och allt bör vara i sin ordning.
Melker
Vid 6 minuter så lyckas du på nåt vänster få att argumentet för i att bli pi/4 borde det inte vara pi/2? Kollade ditt svar och jämförde med WolframAlpha och de stämde inte riktigt överens.
Tack för en bra tjänst 🙂
Melker
Simon Rybrand (Moderator)
Hej Melker och tack för din kommentar. Det verkar ha blivit fel i just denna video och vi ordnar förstås det på momangen. Tack för att du uppmärksammade oss på detta!
Endast Premium-användare kan kommentera.