I den här lektionen går vi igenom s-t-grafen som ett verktyg för att beskriva rörelse. VI tar också upp hur information kan utläsas ur en s-t-graf.
Vad är en s-t-graf?
En rörelse kan beskrivas med hjälp av en sträcka-tid-graf, som förkortat kallas s-t-graf. I en s-t-graf kan vi t ex avläsa var ett föremål befinner sig vid en viss tidpunkt.
Den vertikala axeln visar föremålets position i förhållande till origo, och den horisontella axeln visar hur lång tid som har passerat sedan vi började mäta. Enheterna på axlarna kan variera, men det är alltid en enhet för sträcka på s-axeln och en enhet för tid på t-axeln.
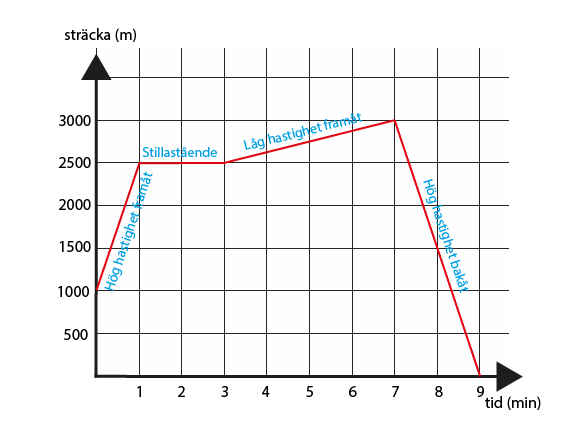
Vad kan vi utläsa ur s-t-grafen?
Ett föremåls rörelse är utritad i figuren nedan. Vi tittar på vilken information vi kan utläsa ur grafen.
-
Föremålets position vid en viss tidpunkt
Vi ser att föremålet var $1000$1000 meter från origo vid tidpunkten $t=0$t=0 , dvs då tiden började mätas. Vi kan avläsa föremålets position vid vilken tidpunkt som helst, exempelvis har föremålet positionen $s=3000$s=3000 m vid tidpunkten $t=7$t=7 min. Genom att avläsa olika positioner vid olika tidpunkter kan vi även bestämma föremålets förflyttning. I detta fall har föremålet förflyttats $Δs=3000-1000=2000$Δs=3000−1000=2000 m under tidsintervallet $Δt=7-0=7$Δt=7−0=7 min.
-
Föremålets hastighet vid en viss tidpunkt
Hur föremålets position ändras i förhållande till tiden är det vi kallar hastighet. Om positionen förändras mycket på kort tid får vi en brantare lutning, dvs en större fart. I s-t-grafen ovan kan vi se att farten i tidsintervallet $0$0 till $1$1 min är större än farten i tidsintervallet $3$3 till $7$7 min, utifrån en brantare respektive flackare lutning.
Om lutningen är konstant (dvs en rät linje) i ett visst tidsintervall, så som i s-t-grafen ovan, innebär det att hastigheten är konstant i detta tidsintervall. Om lutningen är noll (dvs en horisontell linje) innebär det den konstanta hastigheten $0$0 , föremålet är stillastående.
En positiv lutning betyder positiv hastighet, och en negativ lutning betyder negativ hastighet. Vilken riktning som är positiv respektive negativ kan definieras i varje situation, det viktiga är att positiv och negativ innebär just motsatt riktning när det gäller vektorer. Ofta anges uppåt eller framåt som positiv riktning, vilket innebär att nedåt respektive bakåt då tolkas som negativ riktning.
En s-t-graf anger ett föremåls position vid en viss tidpunkt. Vi kan även få information om föremålets hastighet (storlek och riktning) vid en viss tidpunkt.
Exempel
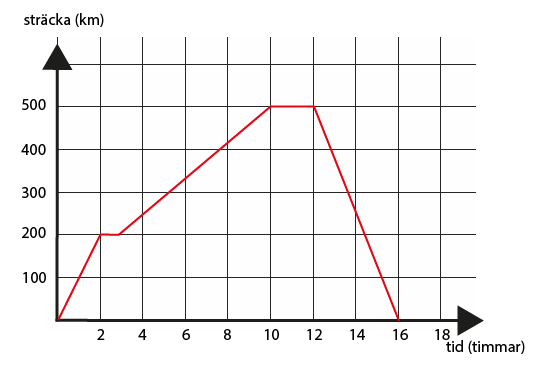
Grafen beskriver en lång bilresa. Använd grafen och avgör följande:
- Startar resan ”hemifrån”?
- När står bilen stilla?
- När har bilen som störst fart?
- Hur långt färdas bilen mellan tidpunkterna $t=4$t=4 h och $t=10$t=10 h?
- Om hastighetsbegränsningen är $90$90 km/h, kör bilen för fort under någon period?
- Var slutar bilresan?
Lösning
- Vi ser att positionen är $s=0$s=0 vid tiden $t=0$t=0 , dvs när resan startar. Detta kan vi tolka som att resan startar ”hemifrån”.
- Vi ser att grafen är horisontell i tidsintervallet $t=2$t=2 till $t=3$t=3 och i tidsintervallet $t=10$t=10 till $t=12$t=12 . Det innebär att hastigheten är $0$0 km/h under dessa perioder. Då står alltså bilen still.
- Lutningen på grafen är brantast mellan $t=12$t=12 och $t=16$t=16 . Då har bilen störst fart. Att linjen lutar nedåt innebär en negativ hastighet, vilket betyder att bilen är på väg tillbaka mot startpunkten.
- Vi ser i grafen att vid tiden $t_1=4$t1=4 h har bilen positionen $s_1=250$s1=250 km, och vid tiden $t_2=10$t2=10 h har bilen positionen $s_2=500$s2=500 km. Det innebär att bilen förflyttas sträckan:
$Δs=s_2-s_1=500-250=250$Δs=s2−s1=500−250=250 km - Vi kan se att under perioden med störst fart färdas bilen $Δs=500$Δs=500 km på $Δt=4$Δt=4 h. Eftersom grafen visar en rät linje innebär detta den konstanta hastigheten:
$v=$v= $\frac{Δs}{Δt}=\frac{500}{4}\text{ }=$ΔsΔt =5004 = $125$125 km/h
Så ja, bilen överskrider hastighetsgränsen. - Efter $16$16 timmar är bilens position $s=0$s=0 km igen, vilket innebär att bilresan slutar där den startar, dvs ”hemma”.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (5)
-
1. Premium
Hur ser man i en s-t-graf att ett föremål är stillastående?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
En brant lutning i en s-t-graf motsvarar:
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
Att en kurvas lutning går från att ha en brant lutning till att vara vågrät innebär att:
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
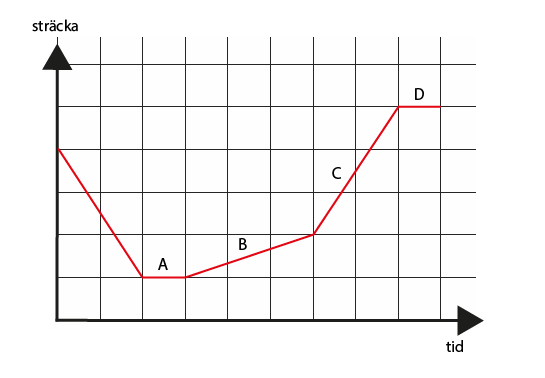Vid vilken tidpunkt är farten som störst?Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
5. Premium
Uppgift från kursprov i Fysik A, VT-2002.
I ett experiment går Moa framför en ultraljudsgivare så att hennes rörelse registreras. Hon befinner sig från början vid punkten R i figuren och står stilla där en stund. Sedan flyttar hon sig längs med linjen till P och stannar där en stund. Därefter går hon snabbt tillbaka till Q, vilar där en stund och återvänder sedan långsamt till R. Vilken av graferna beskriver bäst rörelsen?
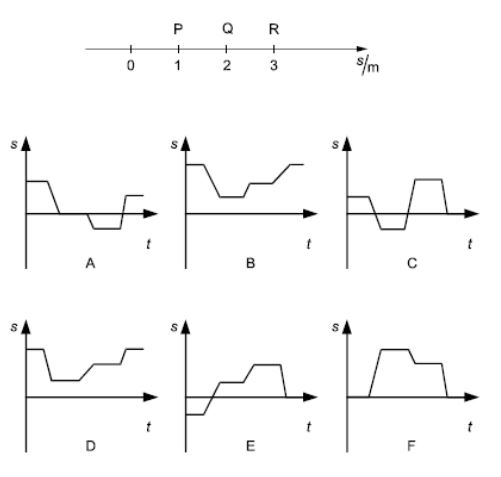Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
Jakub Medynski
Fråga 3:
”Att en kurvas lutning går från att ha en brant lutning till att vara vågrät innebär att:”
den ”rätta” svaren är: ”Föremålets hastighet hökar”, tror det ett stavfel, samt svaret verkar vara ”Föremålets hastighet minskar.”
Simon Rybrand (Moderator)
Hej
Vi kikar på detta och korrigerar.
Endast Premium-användare kan kommentera.