00:00
00:00
KURSER  / 
Fysik 1
/  Krafter
Krafter

Vektoraddition - fysik

Författare:Daniel Johansson
PROVA GRATIS
Så hjälper Eddler dig:
Videor som är lätta att förstå Övningar & prov med förklaringar
Allt du behöver för att klara av nationella provet
PROVA GRATIS
Så hjälper Eddler dig:
Videor som är lätta att förstå Övningar & prov med förklaringar
Allt du behöver för att klara av nationella provet

Innehåll

Exempel i videon

Beräkna resultanten av de två krafterna: F⃗1=(1,5)\vec{F}_1 =(1, 5) samt F⃗2=(3,3)\vec{F}_2=(3, 3)

F⃗1+F⃗2=(1,5)+(3,3)=(1+3,5+3)=(4,8)\vec{F}_1 + \vec{F}_2 = (1, 5) + (3, 3) = (1+3, 5+3) = (4, 8)

Vektoraddition

När flera krafter verkar på ett föremål så behöver vi addera krafterna med varandra för att räkna ut den totala kraften. Vi behöver då använda oss av addition av vektorer. Summan av två vektorer kallas för resultanten.

När man ska addera vektorer med varandra så finns det två olika metoder man kan använda sig av.

Polygonmetoden

Den första metoden är grafisk, dvs vi behöver inte använda oss av några siffror utan endast flytta på våra kraftpilar. Polygonmetoden går ut på att vi flyttar vektorerna som ska adderas så att de sitter ihop. Dvs, där den ena vektorn slutar där börjar den andra.
Resultanten är då den kraftpil som går från origo och pekar på den punkt som den sista kraftpilen pekar på. Ett exempel visas i bilden nedan, där tre krafter adderas med varandra.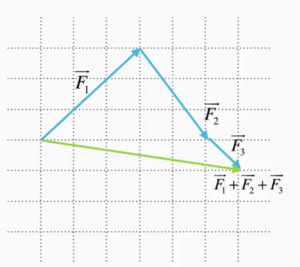
skarmavbild-2016-09-15-kl-13-22-23

Komponentform

För den andra metoden behöver vi inte rita ut våra krafter som pilar. Istället kan vi använda oss av krafternas x- och y-komponenter.

Exempel

Om vi vill addera två vektorer med varandra, t.ex. F⃗1=(2,1)\vec{F}_1= (2,1 ), samt F⃗2=(9,2)\vec{F}_2=(9,2) så kan vi beräkna resultanten genom att addera x-komponenterna med varandra, samt y-komponenterna med varandra. Svaret blir:
F⃗1+F⃗2=(2,1)+(9,2)=(2+9,1+2)=(11,3).\vec{F}_1 + \vec{F}_2 = (2, 1) + (9, 2) = (2+9, 1+2) = (11, 3).

Den allmänna formen för detta är:

Komponentform för vektoraddition

F⃗1+F⃗2=(x1,y1)+(x2,y2)=(x1+x2,y1+y2)\vec{F}_1 + \vec{F}_2 = (x_1, y_1) + (x_2, y_2) = (x_1+x_2, y_1+y_2)

Nästa lektion: Vektorsubtraktion – Fysik

Eddler
VÅR TJÄNST
POPULÄRA KURSER
FÖRETAGSINFO

  • Eddler AB
    Org.nr: 559029-8195
    Kungsladugårdsgatan 86
    414 76 Göteborg

    info@eddler.se
© 2024 EDDLER AB
  • Säker SSL-server