
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1a
/ Trigonometri och Vektorer
Vektor och Skalär
Innehåll
I den här lektionen går vi igenom innebörden av en vektor och en skalär och tittar på parallella och motsatta vektorer. Vi visar även grafiskt hur du parallell förflyttar en vektor till origo.
Skillnaden på en vektor och en skalär
För att att förklara vad en vektor och skalär är, börjar vi med begreppet storhet. En storhet kan beskrivas som egenskapen hos en händelse eller ett föremål som kan jämföras, mätas eller beräknas. En längd, hastighet, vikt eller tid är några exempel på storheter.

Både vektorer och skalärer är storheter, skillnaden är att en vektor även har en riktning och inte bara en kvantitet, alltså en storlek.
Skalär
En skalär kan beskrivas som en storhet som endast har en storlek.
Några exemplen på skalärer är massa, tid och temperatur. Alla har en kvantitet som kan går att mätas. Temperaturen kan öka men ändå befinna sig på samma plats. Skalären representeras av ett tal.
Vektor
En vektor är en storhet som både har en storlek och en riktning.
Några exemplen på vektorer är krafter, hastigheter och en acceleration. Alla har en kvantitet som också har en riktning. Om en bils hastighet ökar, förflyttas den också i någon riktning.
Så skrivs en vektor
När man skall markera att en storhet beskriver en vektor, använder man en liten pil ovanför en bokstav, tex $\vec{v}$ eller $\vec{u}$.
Vill man förtydliga var vektorn har sin start- och slutpunkt kan man istället uttrycka vektorn som $\vec{v} = \vec{AB}$. Då menar man att vektorn har sin startpunkt i $A$ och slutpunkt i $B$.
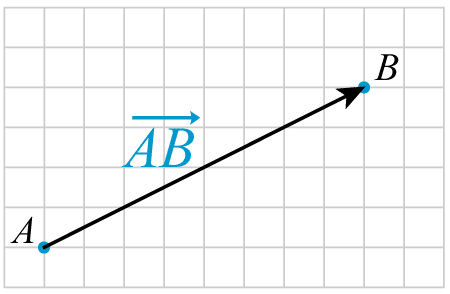
Det finns även andra sätt att skriva vektorer, t.ex. att man fetmarkerar bokstaven, tex $\mathbf{v}$ eller $\mathbf{u}$.
Skalärmultiplikation
För att för ändra en vektors längd kan man multipliceras med en skalär. Vi kommer då att få en ny vektor. Följande gäller för skalärmultiplikation.
- Om vektorn $\vec{v}$ multipliceras med skalären $k\ne1$k≠1 så får vi en ny vektor $k·\vec{v}$ som är $k$ gånger så lång som $\vec{v}$.
- Om $k<0$, dvs om $k$ är ett negativt tal, så får vi en ny vektor med motsatt riktning.
Att multiplicera vektorn med en positiv skalär ger resultatet att vektorn ändrar längd. Vektor ändrar däremot inte riktning. Det enda undantaget är om $k=1$k=1, eftersom att multiplikation med talet ett inte ger någon förändring.
Är skalären däremot negativ, resulterar det i att vektorn får motsatt riktning, alltså behåller samma lutning men pekar med spetsen åt det motsatta hållet. Är skalären inte lika med $\left(-1\right)$(−1) ändras även vektorns längd.
Att multiplicera en vektor med till exempel skalären $2$2 resulterar i att den nya vektorn har samma riktning, men blir dubbelt så lång.
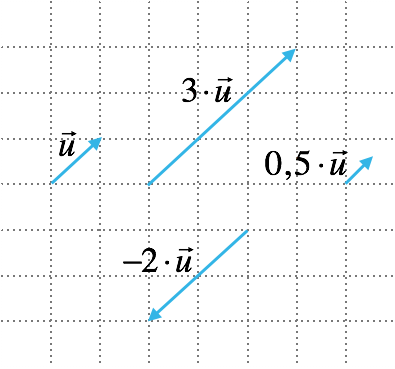
Exempel 1
Multiplicera en vektor $\vec{u}$ med skalärerna $3,\,0,5$ och $-2$ och rita ut de nya vektorerna.
Lösning
Parallella vektorer och Motsatta vektorer
Det är också viktigt att känna till begreppen parallella vektorer och motsatta vektorer då dessa används för att beskriva vektorers förhållande till varandra.
Parallella vektorer
Vektorer som har samma eller motsatt riktning.
Motsatta vektorer
Vektorer som har samma storlek men motsatt riktning.
Vektorn $\vec{z}$ har den motsatta vektorn $\vec{-z}$ och då gäller att $ \vec{z}+(\vec{-z})=\vec{z}-\vec{z}=0 $
Parallellförflyttning av vektorer
Vektorer kan även parallellförflyttas eftersom placeringen av en vektor inte är viktig, vektorn är densamma även om den flyttas. D.v.s. om vi flyttar en vektor så har den fortfarande samma storlek (pilens längd) och riktning (pilens riktning).
Här är det viktigt att känna till att om man parallellförflyttar en vektor till origo så kan denna vektor beskrivas med hjälp av koordinaterna för dess slutpunkt. Om en vektor $\vec{v}$ har sin start i origo och sin slutpunkt i $(a,b)$ så kan denna vektor skrivas som $\vec{v}=(a,b)$.
Exempel 2
Parallellförflytta vektorn i bilden till origo och ange dess koordinater.
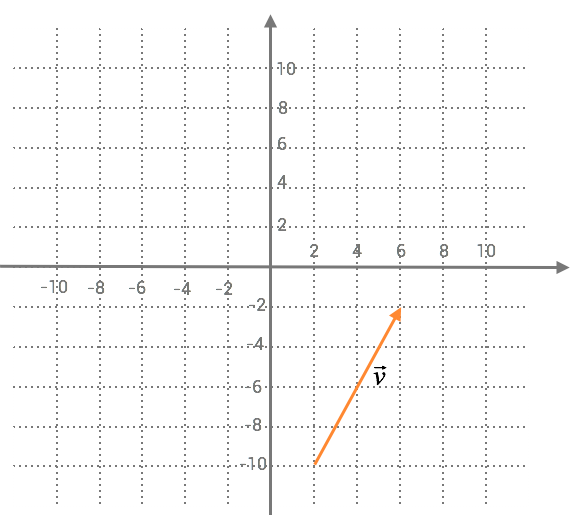
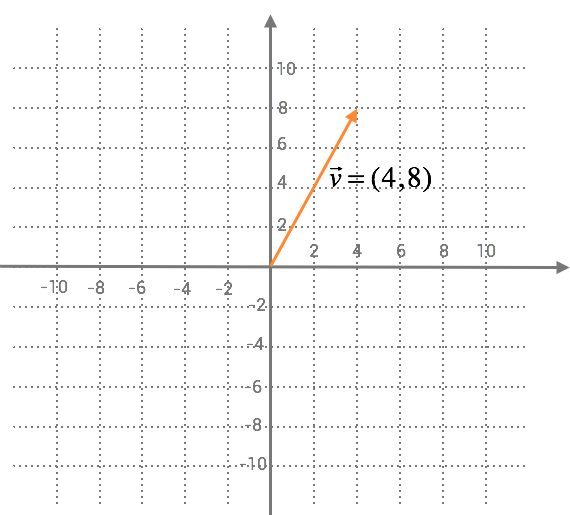
Lösning
Vi sätter vektorns startpunkt i origo och kan skriva denna vektor i koordinatform som $ \vec{v}=(4,8) $ efter som att vektorns spets då avslutas i den punkten.
Exempel i videon
- Exempel på skalärer och vektorer.
- Exempel på utritning (åskådliggöra) vektorer.
- Multiplicering av vektorn $\vec{u}$ med skalärerna $2$ och $-0,5$.
- Exempel på parallella vektorer och motsatta vektorer.
- Parallellförflyttning av vektorerna $\vec{v_1},\vec{v_2}$ och $\vec{v_3}$ till origo.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (9)
-
1. Premium
Vad saknar en skalär som en vektor har?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Matematik 2 Trigonometri och Vektorer Vektor och SkalärRättar... -
2. Premium
Är tid en skalär eller en vektor?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Skalär VektorRättar... -
3. Premium
Är acceleration en skalär eller en vektor?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Skalär VektorRättar... -
4. Premium
En skidåkare har en massa på $92$92 kg med utrustning.
Är denna storhet en skalär eller en vektor?Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Matematik 2 Skalär Trigonometri och Vektorer Vektor Vektor och SkalärRättar... -
5. Premium
Vilket påstående stämmer inte?
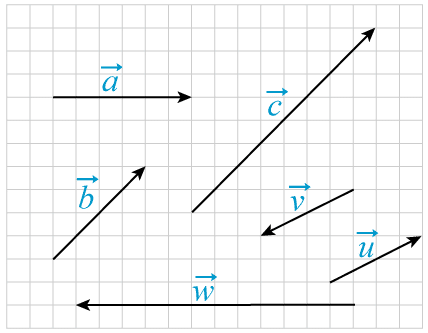 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri ma1 Matematik 1 Matematik 2 parallella vektorer Trigonometri och Vektorer Vektor Vektor och SkalärRättar... -
6. Premium
Vektorn $\vec{z}$→z är utritad längst upp i figuren. Ange vilken av vektorerna $\vec{a},\text{ }\vec{b}$→a, →b eller $\vec{c}$→c representerar resultatet på skalärmultiplikationen $-\frac{1}{3}$−13 $\cdot\vec{z}$·→z
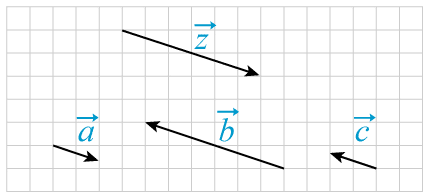 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Matematik 2 Skalär skalärmultiplikation Trigonometri och Vektorer Vektor Vektor och SkalärRättar... -
7. Premium
Rättar... -
8. Premium
En vektor $\vec{v}$→v har sin startpunkt i $(-2,-6)$(−2,−6) och sin slutpunkt i $(-2,2)$(−2,2).
Parallellförflytta denna vektor till origo och ange den på koordinatform.Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Matematik 2 parallellförflyttning Skalär Trigonometri och Vektorer Vektor Vektor och SkalärRättar... -
9. Premium
Vilket påstående stämmer?

Öva på att motivera varför.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Matematik 2 motsatta vektorer Trigonometri och Vektorer Vektor Vektor och SkalärRättar...
c-uppgifter (2)
-
10. Premium
Vektorn $\vec{AB}$→AB har sin startpunkt i $A=(4,-1)$A=(4,−1) och sin slutpunkt i $B=(-3,-5)$B=(−3,−5).
Vilka koordinater får vektorns nya slutpunkt C om vi parallellförflyttar den så att startpunkten är i origo istället? Använd dig gärna av ett koordinatsystem för att lösa uppgiften.Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
11. Premium
Vilken skalärmultiplikation stämmer inte?

Öva på att motivera varför.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Geometri Matematik 1 Matematik 2 motsatta Skalär skalärmultiplikation Trigonometri och Vektorer Vektor Vektor och SkalärRättar...

David Ahlstrom
Det blir error när man har rättat. En enda lång grå sida efter några frågor.
Simon Rybrand (Moderator)
Vi kikade på detta och det skall fungera nu.
Johan
Tjena!
Dubbelfel i uppgift 5.
Fel 1) Enligt koordinatsystemet i facit börjar skalären i (-2, -6) men slutar i (-2, 2) och inte i (-2, -2) som uppgiften anger.
Fel 2) Den flyttade skalären har fått ny koordinat (0, 6) – men bilden visar hur skalären flyttats till (0, 8).
Blev det tydligt? :S 🙂
Simon Rybrand (Moderator)
Hej
Ja det var verkligen ett dubbelfel där 🙂
Tack för att du sade till, det är korrigerat.
Willy
Hej!
Jag tycker inte att denna video ger mig det jag behöver för att kunna lösa dessa uppgifter. Videon går inte igenom vad som är resultant osv, inte heller ger videon genomgång på liknande uppgifter som kommer i övningarna. Eller så är videon inte tillräckligt tydlig nog för mig helt enkelt. Lite feedback bara.
Simon Rybrand (Moderator)
Hej!
Tack för feedback, vi tar självklart till oss av detta! Vi pratar mer om resultant i videon om vektoraddition. Kika även på vektorsubtraktion så kommer din bild fördjupas något till kring området.
Tobias Nilsson
Är fundersam på fråga 4, svaret ar skrivet i förklaringen, men svarar man det så får man fel på frågan? (Roten ur 2 är förklaringens korrekta svar men svarsalternativet 3 ger rätt svar på frågan)
Set också att additionen i förklaringen är inkorrekt:
”
Adderar vektorerna: (0, -2) + (3,2) + (-4,-1) = (0+3-4, -2+2-1) = (-1, 1)
”
Borde inte -2+2-1 bli -1 så den resulterande vektorn blir (-1,-1)?
Gillar verkligen alla förklaringar, webbplatsen och videos i allmänhet, de har verkligen hjälpt, men det är ibland små saker som dessa som gör att man spenderar mer tid än nödvändigt, framförallt om man tror att man själv har fel och jagar lösningar i jakten på förståelse. 🙂
Simon Rybrand (Moderator)
Hej Tobias
Det var fel i den uppgiften och det är nu korrigerat, tack för att du sade till!
Förstår att det kan vara irriterande att känna att man har lagt mer tid än vad man borde på en uppgift. Så ber om ursäkt för detta fel och har inga andra ursäkter än att vi hanterar några tusen uppgifter som vi konstruerar själva och att det ibland blir fel helt enkelt. Tack för att du tog dig tid och kommenterade detta!
Pedro Veenekamp
Hej!
Jag förstår inte riktigt övningen 4. Om systemet börjar på punkten (1,3) varför plussar du vektorernas slutpunkter som om de började ifrån origo?
Att subtrahera systemets startpunkten av resultatet ger en vektor som inte resulterar från summan av de tre vektorerna.
Följande länk (GeoGebra) kanske förklarar bättre hur jag tänkte: http://ggbtu.be/m718365
Tack i förhand!
Simon Rybrand (Moderator)
Hej
Det är fel förklarat i den uppgiften. Har uppdaterat denna med en korrekt förklaring. Gör där så att vi först flyttar alla vektorer till origo för att sedan summera dessa. Därefter beräknas resultantens längd med hjälp av pythagoras sats.
(P.S detta var en gammal uppgift vi har plockat in och inte hunnit kontrollera, ber om ursäkt för detta och tackar samtidigt att du tar dig tid att ställa frågor och påpeka liknande saker som denna. Kul också att du använder dig av Geogebra!)
Willy
Jag förstår inte riktigt svarte på övning 4. Som sagt tror jag inte att jag fick nog kunskap av videon. Hur flyttar du dessa till origo? Du både adderar och subtraherar. Kan du gå igenom hur du kommer fram till: (0,−2)
(3,2)
(−4,−1)
Kanske vore bra med att du visar hur du subtraherar?
Willy
*svaret*
Simon Rybrand (Moderator)
Hej, Vi får nog göra så att vi flyttar denna övning till lektionen om vektoraddition. Där blir det nog mer tydligt hur man kan göra dessa operationer.
maggix
Hej!
Tycker frågorna på den här filmen skulle passa bättre på vektoradditionsvideon. Förstod inget när du börja prata om flera vektorer och vad deras resultanten är och du nämner det inte heller i videon. Sen tittade jag på additionsvideon och där förklara du det jätte bra och då förstod jag!
Simon Rybrand (Moderator)
Tack för bra feedback, vi skall kika på om vi kan förbättra upplägget på frågorna här!
Birgitta Högström
Hej!
Under videon: Vektor och Skalär, ca 6 min in, så är vektorerna inte riktigt rätt riade(parallella Vektorer)
Mvh Birgitta
Simon Rybrand (Moderator)
Hej,
Är det de tre parallella vektorerna som har samma lutning som du menar är felritade? Eller där vi visar skalärmultiplikation?
MAXI
Uppgift 2 innehåller samma fel som tidigare uppgift 4, alltså pythagoras sats skrivs fel i lösningsförklaringen.
Simon Rybrand (Moderator)
Tack för kommentaren, det är åtgärdat!
nti_ma1
Uträkningen enl pythagoras sats i fråga 4 är fel. Kateternas kvadrater skall väl adderas under rottecknet?
Simon Rybrand (Moderator)
Hej! Tack för att du kommenterade detta, vi har åtgärdat det!
Endast Premium-användare kan kommentera.