
Innehåll
OBS! LEKTIONEN ÄR UNDER UPPBYGGNAD!
Vi ska i den här lektionen titta på hur laddade partiklar beter sig när de befinner sig i magnetfält. Vi har i tidigare lektioner sett att en laddning som befinner sig i ett elektriskt fält påverkas av elektriska krafter. Något liknande händer på en laddad partikel befinner sig i ett magnetfält. Men en stor skillnad mellan laddade partiklar i elektriska fält och i magnetfält är att för att magnetfältet ska påverka laddningen med krafter så måste laddningen röra sig i fältet.
Vi kan nu få en något djupare förklaring till det vi såg i en tidigare lektion, nämligen att en elektrisk ledare som befinner sig i ett magnetfält påverkas av en magnetisk kraft. Det beror alltså på att det i ledaren går en ström, dvs. elektroner som ju är laddade partiklar i rörelse. Elektronerna rör sig ju då i magnetfältet även om de råkar vara ”fast” i ledaren och påverkas därmed av en liten magnetisk kraft. Eftersom det rör sig väldigt många elektroner genom ledaren så gör deras gemensamma kraftpåverkan att ledaren som helhet påverkas av en kraft.
Kraftens storlek
Men vad påverkar hur stor kraft laddningarna påverkas av?
Genom ledaren går ju en ström och om vi tittar på definitionen av ström så är ju den laddningsmängd som passerar ett tvärsnitt av ledaren per sekund, eller uttryckt matematiskt: $I=\frac{\bigtriangleup Q}{\bigtriangleup t}$I=△Q△t .
Vi kan ju även skriva laddningen som passerar tvärsnittet som antalet elektroner multiplicerat med elektronladdningen, dvs. $Q=N\cdot e$Q=N·e . Och om ledarens längd i magnetfältet är $l$l så kan man ju tänka på det som en viss sträcka som elektronerna ska färdas på tiden $\bigtriangleup t$△t och vi kan använda vår gamla sträckformel $s=vt$s=vt och skriva $l=v\bigtriangleup t\Rightarrow\bigtriangleup t=\frac{l}{v}$l=v△t⇒△t=lv . Vi sätter in detta i uttrycket för strömmen:
$I=\frac{\bigtriangleup Q}{\bigtriangleup t}=\frac{\bigtriangleup Q\cdot v}{l}$I=△Q△t =△Q·vl
Från en tidigare lektion vet vi att kraften på en strömförande ledare i ett yttre magnetfält ges av $F=IlB$F=IlB. Vi kan då skriva kraften per elektron som $F=\frac{IlB}{N}$F=IlBN , där $N$N är antal elektroner som i varje ögonblick befinner sig i ledaren inom magnetfältet. Vi ersätter strömmen $I$I med uttrycket vi nyss tog fram och efter lite förenkling av uttrycket får vi att kraften som en elektron påverkas med då den rör sig i ett magnetiskt fält kan skrivas $F=evB$F=evB.
Vi kan nu generalisera detta att gälla vilken laddad partikel $q$q som helst och vi får till sist:
Magnetisk kraft på en laddad partikel som rör sig i ett magnetfält
$F=qvB_{\perp}$F=qvB⊥
där $F$F är kraften som en laddad partikel med laddningen $q$q och hastigheten $v$v påverkas av då den rör sig genom ett magnetfält med flödestätheten $B$B.
Notera att laddningens hastighetsriktning och magnetfältets riktning måste vara vinkelräta mot varandra. Är de inte det så måste vi komposantuppdela och endast räkna med den vinkelräta komposanten.
Kraftens riktning
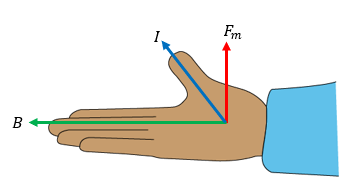
Vi ska nu se om vi kan lista ut hur kraften är riktad. Vi kan använda samma högerhandsregel som vi använde för kraftriktningen på en strömförande ledare i ett yttre magnetfält. Eftersom laddningar i rörelse i praktiken är vad vi brukar kalla ström så låter vi återigen högra handens tumme vara i strömmens riktning, och kom nu ihåg att strömriktningen är definierad som den riktning som positiva laddningar rör sig i.
Sedan låter vi fingrarna vara i magnetfältets riktning, och då får vi kraften på laddningen i handflatans riktning enligt figuren här.
Det här gäller alltså för POSITIVA laddningar. Om vi vill bestämma kraftens riktning på negativa laddningar som t.ex. elektroner så måste vi komma ihåg att strömmens riktning då blir den motsatta dvs. högra handens tumme blir ju då riktad motsatt elektronernas rörelseriktning.
.
Exempel 1
En elektron befinner sig i ett magnetfält enligt figuren. Magnetfältet har en magnetisk flödestäthet på $50$50 μT och elektronens hastighet är $3,0$3,0 Mm/s. Hur stor kraft påverkas elektronen av och hur är kraften riktad?
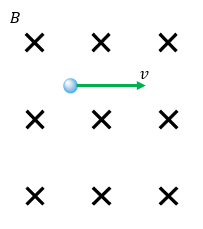
Lösning
Kraftens storlek:
Vi använder uttrycket $F=qvB_{\perp}$F=qvB⊥.
Vi ser i figuren att hastigheten och magnetfältet är vinkelräta mot varandra så vi behöver inte komposantuppdela och laddningen är ju en elektron så vi kan skriva att kraften är $F=evB$F=evB.
Vi sätter in värden, elektronens laddning är ju $e=1,602\cdot10^{-19}$e=1,602·10−19 C, hastigheten är $v=3,0\cdot10^6$v=3,0·106 m/s och den magnetiska flödestätheten är $50$50 μT:
$F=evB=1,602\cdot10^{-19}\cdot3,0\cdot10^6\cdot50\cdot10^{-6}\approx2,4\cdot10^{17}$F=evB=1,602·10−19·3,0·106·50·10−6≈2,4·1017 N.
Kraftens riktning:
Vi använder högerhandsregeln:
Vi riktar högra handens tumme i strömriktningen, dvs. motsatt elektronens riktning vilket blir åt vänster i figuren. Sedan riktar vi högra handens fingrar i magnetfältets riktning, dvs. in i skärmen, då får vi kraften på laddningen i handflatans riktning, dvs. nedåt i figuren.
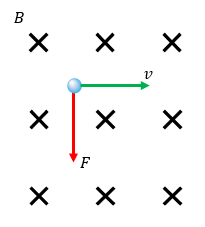
Svar
Vi får att kraften är ca $2,4\cdot10^{17}$2,4·1017 N, riktad rakt nedåt i figuren.
Styra laddade partiklar
Det här innebär att laddade partiklar som kommer in i ett magnetfält med hastigheten vinkelrät mot magnetfältets riktning kommer att böja av och börja färdas i en cirkelrörelse.
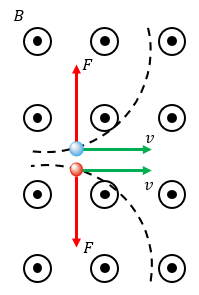
I figuren så är magnetfältet riktat ut ur pappret vilket innebär att en negativt laddad partikel med hastigheten riktad från vänster till höger kommer att påverkas av en kraft riktad uppåt, kontrollera själv med högerhandsregeln, medan en positivt laddad partikel påverkas av en kraft riktad nedåt.
Allteftersom partiklarna böjer av så ändras ju strömriktningen vilket då även påverkar kraftriktningen vilket i sin tur gör att den magnetiska kraften på partiklarna agerar centripetalkraft och partiklarna böjer av i cirkelbanor. Testa även det här med högerhandsregeln. Detta gör att vi kan styra laddade partiklar i olika praktiska tillämpningar genom att använda lämpliga hastigheter och flödestätheter.
Hastighetsfilter
En tillämpning av detta är att man kan skapa ett ”hastighetsfilter” och filtrera ut partiklar som har en viss hastighet. För att göra detta behöver vi ”korsa” två fält, ett elektriskt fält och ett magnetiskt. Vi tänker oss därför ett homogent elektriskt fält med fältstyrkan E mellan två laddade plattor med den positiva plattan överst. En elektron som kommer in i fältet med en hastighet vinkelrät mot fältet kommer därmed att påverkas av en elektrisk kraft $F_e=qE$Fe=qE uppåt. Vi lägger även ett magnetfält vinkelrätt över det elektriska fältet, riktat in i skärmen. Elektronen kommer då även att påverkas av en magnetisk kraft $Fm=qvB$Fm=qvB, riktad nedåt i figuren.
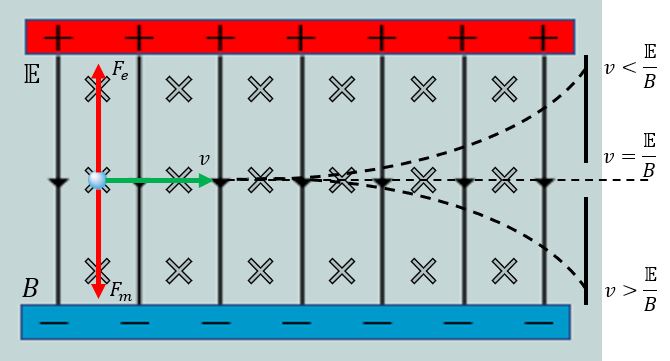
I slutet av området med de två fälten så lägger vi ett hinder med en liten öppning i mitten. Om nu den elektriska kraften är större än den magnetiska så kommer ju elektronen att avlänkas uppåt och därmed inte ta sig ut ur hindret. Motsvarande gäller om den magnetiska kraften är större än den elektriska.
Men om de båda krafterna är lika stora så kommer ju elektronen att färdas rakt framåt och ta sig ut ur öppningen i hindret. Att krafterna är lika stora innebär ju att $F_e=F_m$Fe=Fm, dvs. $qE=qvB$qE=qvB. Vi förkortar bort laddningen $q$q och löser ut hastigheten $v$v. Vi får att $v=\frac{E}{B}$v=EB , dvs. endast de partiklar som har en hastighet som är $\frac{E}{B}$EB kommer ta sig ut genom hindret. Vi har skapat ett hastighetsfilter, dvs. ett sätt att sortera ut partiklar med en viss hastighet. Om hastigheten är mindre än eller större än $\frac{E}{B}$EB så missar de öppningen.
Centralrörelse i magnetfält
Vi har sett att eftersom laddningar i magnetiska fält påverkas av en konstant kraft som är vinkelrät mot hastigheten så kommer laddningen att böja av radiellt, dvs. i en centralrörelse. Den kraft som agerar centripetalkraft är ju då den magnetiska kraften, dvs. $F_m=F_c$Fm=Fc. Detta gör att vi kan ställa upp Newtons andra lag för cirkelrörelse på följande sätt: $qvB=\frac{mv^2}{r}$qvB=mv2r . Om vi sedan löser ut radien så får vi att den blir $r=\frac{mv}{qB}$r=mvqB .
Vi ser att hur stor centralrörelsen blir, dvs. hur stor radie den får, beror på massan, hastigheten, laddningen och magnetfältet. En större massa och hastighet ger en större radie medan en större laddning och större magnetisk fältstyrka ger en mindre radie. Om vi löser ut massan ur sambandet så inser vi kanske att detta kan användas för att ”väga” en laddad partikel
$m=\frac{qBr}{v}$m=qBrv .
Vi låter en partikel med känd laddning och hastighet komma in i ett magnetfält med känd flödestäthet. Partikeln kommer ju då att utföra en cirkelrörelse enligt figuren. Vi mäter sedan avståndet $d$d mellan öppningen och nedslagspunkten $P$P. Detta avstånd är ju centralrörelsens diameter och därmed vet vi indirekt radien och kan då beräkna partikelns massa.
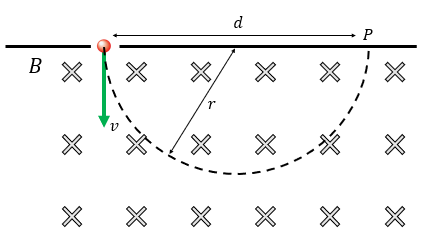
En sådan här uppställning kallas en masspektrometer.
Exempel 2
Vi låter en partikel med laddningen $+2e$+2e och hastigheten $0,11\text{ }$0,11 Mm/s komma in i ett magnetfält med en flödestäthet på $20$20 mT enligt figuren ovan. Avståndet $d$d uppmäts till $11,4$11,4 cm. Vad väger partikeln?
Lösning
Vi sätter in värden i uttrycket för massan:
$m=\frac{qBr}{v}=\frac{2\cdot1,602\cdot10^{-19}\cdot20\cdot10^{-3}\cdot\left(\frac{0,114}{2}\right)}{0,11\cdot10^6}\approx3,3\cdot10^{-27}$m=qBrv =2·1,602·10−19·20·10−3·(0,1142 )0,11·106 ≈3,3·10−27 kg
Svar
Partikeln väger ca $3,3\cdot10^{-27}$3,3·10−27 kg.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████

Endast Premium-användare kan kommentera.