00:00
00:00
KURSER  / 
Fysik 1
/  Krafter
Krafter

Vektorer och trigonometriska funktioner

Författare:Daniel Johansson
PROVA GRATIS
Så hjälper Eddler dig:
Videor som är lätta att förstå Övningar & prov med förklaringar
Allt du behöver för att klara av nationella provet
PROVA GRATIS
Så hjälper Eddler dig:
Videor som är lätta att förstå Övningar & prov med förklaringar
Allt du behöver för att klara av nationella provet

Innehåll

Exempel i videon

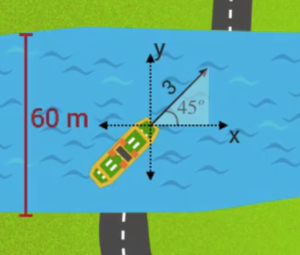
skarmavbild-2016-10-06-kl-12-42-46

En båt färdas med en fart på 3,03,0 m/s i en riktning som visas på bilden. Den ska över en kanal som är 6060 m bred. Hur lång tid tar det?

Vi är intresserade av hastighetens y-komponent. Denna kan vi beräkna genom att använda sinus-funktionen.

vy=3⋅sin⁡(45)=2,1m/sv_y = 3 \cdot \sin(45) = 2,1 m/s.

Sträckan som båten ska färdas i y-led är 60 meter. Vi får då tiden:

t=sv=602,1=29s.t = \frac{s}{v} = \frac{60}{2,1} = 29 s.

Svar: Tiden det tar är 29 sekunder.

Att beräkna en vektors komponenter

Det är ofta bra att veta vad en vektor har för komponenter (t.ex. när vi vill addera eller subtrahera två vektorer med varandra). Men i vissa situationer vet man bara en vektors längd och riktning i form av en vinkel till x-axeln. Därför är det bra att veta hur man från detta kan beräkna vektorns komponenter. För att beräkna en vektors komponenter från längden och vinkeln hos vektorn behöver man använda sig av de trigonometriska funktionerna cosinus och sinus. För att åskådliggöra hur detta fungerar kan man måla en rätvinklig triangel under vektorn.

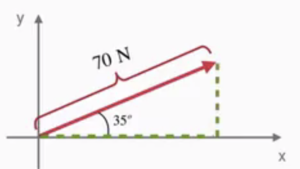
skarmavbild-2016-10-06-kl-12-33-50

Att beräkna x- och y-komponenten

I bilden ovan ser vi att x-komponenten utgör den närliggande kateten, medan y-komponenten utgör den motstående kateten.

Från detta kan vi dra slutsatsen att:

x=70⋅cos⁡(35)=57  Nx = 70 \cdot \cos(35) = 57 \;N

y=70⋅sin⁡(35)=40  Ny = 70 \cdot \sin(35) = 40 \;N

Nästa lektion: Newtons första lag

Eddler
VÅR TJÄNST
POPULÄRA KURSER
FÖRETAGSINFO

  • Eddler AB
    Org.nr: 559029-8195
    Kungsladugårdsgatan 86
    414 76 Göteborg

    info@eddler.se
© 2024 EDDLER AB
  • Säker SSL-server